Advent of Code 2018 Day 18
Try the simulator using your puzzle input!
Task: Solve for X where...
Part 1
X = the total resource value of the lumber collection area after 10 minutes
Part 2
X = the total resource value of the lumber collection area after 1000000000 minutes
Example input
.#.#...|#.
.....#|##|
.|..|...#.
..|#.....#
#.#|||#|#|
...#.||...
.|....|...
||...#|.#|
|.||||..|.
...#.|..|.
It represents:
- A lumber collection area
-
.s are open spaces -
|s are trees -
#s are lumberyards
Part 1
- Another one of these puzzles!
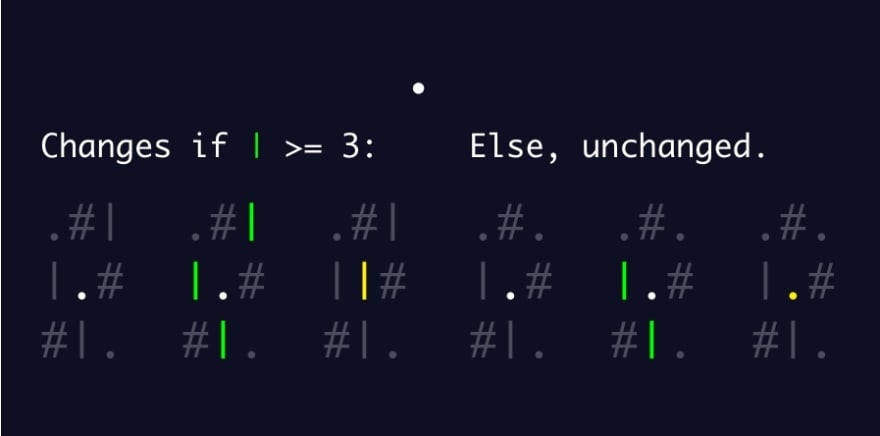
- The rules for what causes a cell's value to change or remain unchanged
- Writing a working algorithm in record speed
Another one of these puzzles!
You know the type:
- A rectangular area
- Where cells contain one of a handful of values
- In each
step, all cells determine whether their value changes based on some or all nearby cells - At the end of each
step, all cells queued to change actually change - Part 1 verifies state after a handful of
stepsto confirm an algorithm works as expected - Part 2 is often a performance test - with an optional twist in the rules - serving as the real puzzle
Since I've solved several of these types of puzzles thus far, I'm confident in my likelihood at solving Part 1, and excited that I might solve Part 2.
The rules for what causes a cell's value to change or remain unchanged
Writing a working algorithm in record speed
- I wrote - from scratch - an algorithm that generated the correct answer for both the example input and my puzzle input
- It took me about 25 minutes to write
I confirmed it worked at a few checkpoints:
- After writing the full nested loop to check each cell and the part that updated each queued cell...to confirm what I saw
After 2 minutesfor the example input matched the instructions - After writing the third, outer, loop that performed the above loops ten times...to confirm what I saw
After 10 minutesfor the example input matched the instructions - After writing the last part that extracted tallies of each character in the final state of the grid and calculated the product of the tallies for trees and lumberyards...to confirm what I saw for the example input matched the instructions
After confirming all this, I swapped the text file I was reading from the example to my puzzle input.
I ran the program.
I copy-pasted and submitted the answer that displayed.
And I was awarded one gold star!
Part 2
- Just as I guessed: a
performancepuzzle, or is it? - Building a simulator to see the grid changing
- Spotting the repeating pattern
- Attempting to do the math to identify the 1-billionth minute's state
- A drawn-out process of elimination and manual binary search
Just as I guessed: a performance puzzle, or is it?
- Forget 10 minutes later
- Try 1 billion minutes later!
- This seems like the program would never finish
- That leads me to want to identify some repeating states of the grid
- Because if I can confirm that one or more states repeat at the same interval, then I can expand those cycles out to near 1 billion minutes and account for the offset
This could be interesting.
Or a bummer, if that's not the key to this puzzle.
As an initial test:
- I upped my iteration count from 10 to 1000
- I created an array that would store each state
- I added the state of the grid at the end of each iteration to the array
- Before adding, I checked whether the array included the new state - confirming it repeats at least once
- If it did, I logged the index of the first occurrence of the repeating state
When running my new algorithm:
- The first repeating state happened around index 560
- It seemed like every state after that was repeating, too. Hmm.
I really needed a better way to see the grid changing.
Building a simulator to see the grid changing
- This would be my first simulator for 2018!
- Luckily, I've built several just like it in past years
- It should take no time at all, since I've already written the code in such a way that can be re-factored to leverage an external iteration counter
Roughly 20 minutes later, I had a working simulator that showed each passing minute of the grid.
Spotting the repeating pattern
Letting it run a few seconds revealed what I had expected:
- A point at which the entire grid re-cycles through the same series of states
Attempting to do the math to identify the 1-billionth minute's state
Now for the tough part:
- Count the length of each cycle
- Devise an equation to calculate the correct offset from an early minute toward the 1-billionth minute
- Do more math to confirm my results
I stamped into memory one of the states of the grid after several hundred minutes.
I then used my simulator's Next button to walk one minute at a time until I saw that stamped state again.
Viola! 34 states between cycles!
This means:
- The state after minute 723
- Is the same as the state after minute 758
- Is the same as the state after minute 793
So, a new cycle starts every 35 minutes.
Next, I needed a number divisible by 35 and 1000000000.
Well:
1000000000 / 35 = 28571428.57...
If I lob off the remainder:
35 * 28571428 = 999999980
That means I need 20 more to get a billion.
What am I looking for again?
I think I need to find X, where...
X + (35 * 285714??) = 1000000000 + some number divisible by 35
My simulator had been running while I was doing this math.
When paused again, it was at close to 700 minutes
I tried this in the console:
685 + (35 * 28571428)
That was a few hundred over 1 billion.
I started fiddling with the numbers until I saw 1 billion exactly.
Eventually, I arrived at this equation equaling 1 billion:
720 + (35 * 28571408)
What was this telling me?
- At the 720th minute, the state should be the same as at the 1-billionth minute
720 happened to be 35 greater than 685, which my simulator was already paused on.
My simulator already showed the resource value at each minute.
I copy-paste and submitted it:
Too low
Bummer. What now?
A drawn-out process of elimination and manual binary search
- I knew the correct answer was one of 35 possible integers
- I knew the answer I entered was too low
- I needed to find the subset of 35 possible integers that were greater than the one I entered
Here is my list, using the minutes counting up to the next cycle in my simulator: 720:
713: 107068
714: 108864
715: 109152
716: 110208
717: 110396
718: 109347
719: 107912
720: 106477
Here they are in order:
106477 - Too low
107068
107912
108864
109152 - Let's try this next, since it's in the middle!
109347
110208
110396
Copy. Paste. Submit.
106477 - Too low
107068
107912
108864
109152 - Too high
109347
110208
110396
Good news: it must be one of three numbers
A better strategy than trying all three?
- The number I tried corresponded to minute 720
- The next number higher corresponds to minute 719
- Maybe I've been
1-offthis whole time - Maybe
after 1000000000 minutesrequired me to find the value when my minute counter was999999999
So, I tried the number corresponding to minute 719:
106477 - Too low 720
107068
107912 - Correct!
108864
109152 - Too high 715
109347
110208
110396
I did it!!
- I solved both parts!
- I made my first simulator in 2018, which helped me find the correct answer for Part 2!
- I made a few diagrams that helped me solidify my understanding of the rules
A familiar-themed puzzle just helped me 'get my groove back'.
On to the next one!






Top comments (0)