Advent of Code 2020 Day 15
Task: Solve for X where...
X = the Nth number in a growing sequence of spoken numbers
- N = 2020
- N = 30000000
Example input
0,3,6
It represents:
- Three turns where each turn that number is spoken
Part 1
- Writing the rules as pseudocode
- Visualizing the example input after 10 turns
- Writing a working algorithm
Writing the rules as pseudocode
For each number
Perform a turn where that number is spoken
For each turn thereafter
If the previous turn's number was never spoken before
Say 0 and end turn
Else - the previous turn's number has been spoken at least once before
Calculate the difference between the turn number of when it was most recently spoken - the previous turn's number - and the most recent time it was spoken prior to that
Say that number and end turn
Visualizing the example input after 10 turns
Input:
0,3,6
Turn 1:
0,
Turn 2:
0,3
Turn 3:
0,3,6
Turn 4:
0,3,6,?
6<-
-,-
0,3,6,0
Turn 5:
0,3,6,0,?
0<-
0,-,-
1 4
4-1 = 3
0,3,6,0,3
Turn 6:
0,3,6,0,3,?
3<-
-,3,-,-
2 5
5-2 = 3
0,3,6,0,3,3
Turn 7:
0,3,6,0,3,3,?
3<-
-,-,-,-,3
5 6
6-5 = 1
0,3,6,0,3,3,1
Turn 8:
0,3,6,0,3,3,1,?
1<-
-,-,-,-,-,-
0,3,6,0,3,3,1,0
Turn 9:
0,3,6,0,3,3,1,0,?
0<-
-,-,-,0,-,-,-
4 8
8-4 = 4
0,3,6,0,3,3,1,0,4
Turn 10:
0,3,6,0,3,3,1,0,4,?
4<-
-,-,-,-,-,-,-,-
0,3,6,0,3,3,1,0,4,0
10th number is 0
Writing a working algorithm
Split the input into an array of strings
Coerce each string into a number
For i from the length of the array up to but not including 2020
Generate one of two numbers:
1. A positive integer if the most recent number is found elsewhere in the array
2. -1 if the most recent number is not found elsewhere in the array
If that number is positive
Add at the end of the array of numbers the difference between the last location of the most recent number and the second-to-last location of the most recent number
Else - the number is -1
Add at the end of the array the number 0
Return the last number in the array
This puzzle helped me learn a new way to leverage JavaScript's multi-purpose method, lastIndexOf().
- Passing a second, optional, argument limits the scope of the search to a subset of the original string or array
So, my algorithm uses this to find the second-to-last index of the most recent number:
let secondToLastIndex = list.lastIndexOf(
list[list.length - 1],
list.length - 2
)
Part 1: Writing a more performant algorithm
- The algorithm above is fast enough for the first couple thousand numbers spoken
- But with each new number spoken, it must maintain and create near-identical lists of n and n-1 numbers spoken length with each iteration
- That's a lot of unnecessary data to manage
The smarter approach: use memoization
- When determining the next number, we only care about two values for each number previously spoken: last occurrence, and the occurrence prior, if any
- Any and all occurrences before those two are unimportant
Here's a scenario using this new algorithm
Given starting numbers:
1,3,2
Our memo starts as:
1: [1,1]
3: [2,2]
2: [3,3]
We will also keep track of the last number spoken:
2
On the next turn:
Turn 4:
Last number spoken: 2
Look-up 2 in memo: [3,3]
Subtract element 2 from element 1: 3-3 = 0
Is 0 a key in memo? Y/[N]
Add it as a key with value: [turn number, turn number]
[4, 4]
Update last number spoken to: 0
Our memo is now:
1: [1,1]
3: [2,2]
2: [3,3]
0: [4,4]
On the next turn:
Turn 5:
Last number spoken: 0
Look-up 0 in memo: [4,4]
Subtract element 2 from element 1: 4-4 = 0
Is 0 a key in memo? [Y]/N
Update it's value to: [turn number, element in location 1]
[5, 4]
Update last number spoken to: 0
Our memo is now:
1: [1,1]
3: [2,2]
2: [3,3]
0: [5,4]
On the next turn:
Turn 6:
Last number spoken: 0
Look-up 0 in memo: [5,4]
Subtract element 2 from element 1: 5-4 = 1
Is 1 a key in memo? [Y]/N
Update it's value to: [turn number, element in location 1]
[6, 1]
Update last number spoken to: 0
Our memo is now:
1: [6,1]
3: [2,2]
2: [3,3]
0: [5,4]
As this plays out:
- The memo grows occasionally, only when the result of a subtraction creates a number that doesn't exist as a key
- More often, a two-element array is updated with two new values
- Gone is the constantly-growing list of numbers to track, and it's one-element-fewer duplicate
Comparing algorithms:
To determine the 100,000th number spoken
- Algorithm 1 takes a few seconds
- Algorithm 2 takes a few milliseconds
Part 2
- As anticipated, this part is a stress test
- I'm glad I refactored my algorithm to drastically improve performance
- Sadly, even my new algorithm would take ages to generate the correct answer
Unaware of a better-performing algorithm, I looked up how my go-to JavaScript solver, NullDev, solved this puzzle.
How another solver's algorithm works
- There appears to be a clever use of array index as the number spoken and its value as the last (or second-to-last?) time it was spoken
- This creates one large array once, and each iteration performs two look-ups and two assignments
- The example answers are generated within a second!
Create an array of length N where N is the target number spoken
Process the input string into an array of numbers
Initialize a current number to 0
For i from 0 to N - 1
If i is within the bounds of the input array of numbers
Set the current number equal to the number at location i in the input array of numbers
Set the value at the location equivalent to current number in the target number array to: i + 1
Else - if i is beyond the bounds of the input array of numbers
Store one of two numbers in a variable, prev:
Either the number at the location in the target number array that is equivalent to the current number
Or -1 if that location does not exist
Update the number at the location in the target number array that is equivalent to the current number to: i
Update the current number to one of two numbers:
1. 0, if prev is -1
2. i - prev, if prev is not -1
Return the current number
Visualizing it helped me better understand how it worked. Especially the setting of either a number or -1 depending on whether the item at the current number index was 0 or any other number.
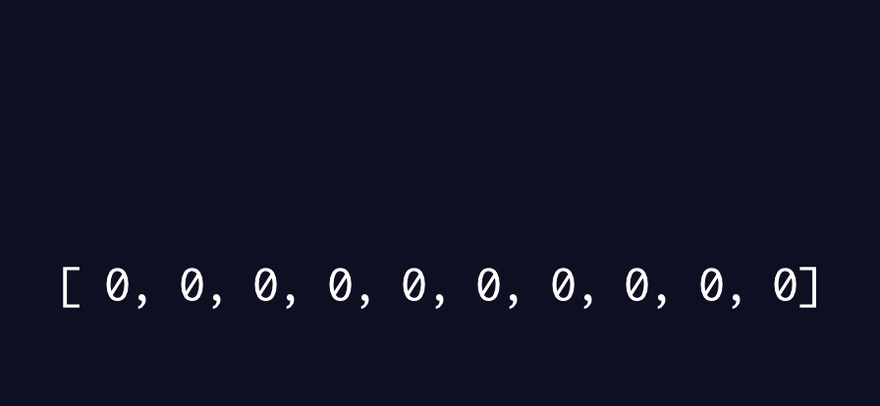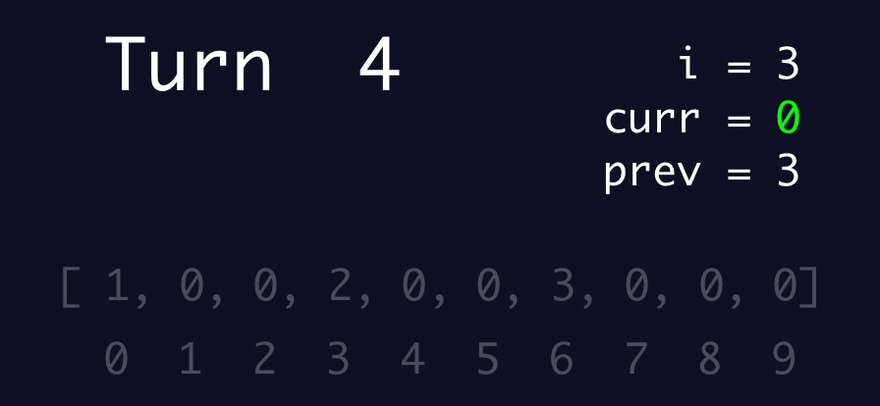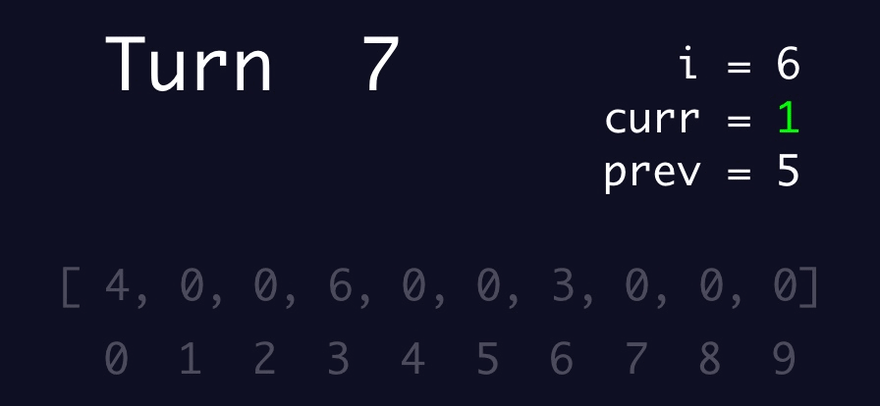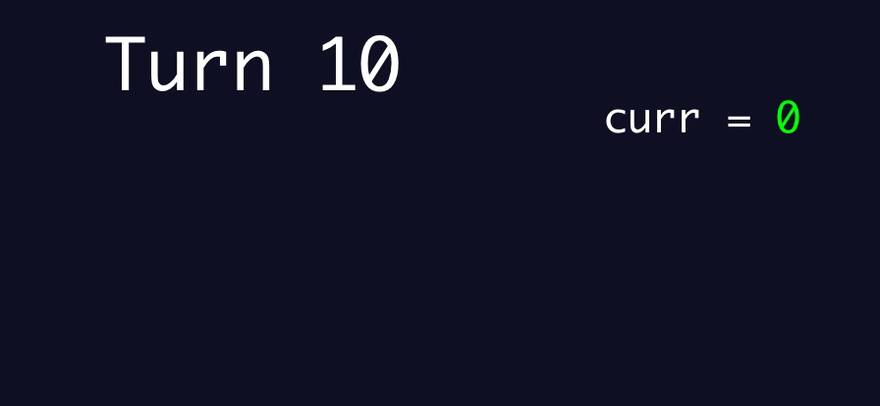
Since I was able to re-product NullDev's algorithm and better understand after visualizing it, I ran my copy-cat algorithm to generate a correct answer for Part 2.
I'll consider that my reward for writing three algorithms: two of my own, and a third without referencing the source at any point while re-creating it.



Top comments (0)