Advent of Code 2020 Day 12
Try the simulator for Part 1!
Task: Solve for X where...
X = the sum of the absolute values of the east/west and north/south distances from the ship's starting position
Example input
F10
N3
F7
R90
F11
It represents
- A series of movements and rotations
- Notated as a single-character action and an integer value
Part 1
- A regular expression to extract action and value
- A data structure for X- and Y- axes
- A data structure for rotation
- A data structure that maps rotation to movement
- Altogether to form a working algorithm
- Building a ship voyage simulator
A regular expression to extract action and value
- For each line, I need the first character and the integer represented by the combination of digits that follow
/(\w)(\d+)/g
This works, but it could be more specific since I know the subset of characters that are the only possibilities: NSEWLRF
/([NSEWLRF])(\d+)/g
A data structure for X- and Y- axes
- The example offers a typical walkthrough of a solution
- I added the array-pair at the end to indicate how I think the current distance from the start could be represented
F10 = east 10, north 0 -> [10, 0] E
N3 = east 10, north 3 -> [10, 3] E
F7 = east 17, north 3 -> [17, 3] E
R90 = east 17, north 3 -> [17, 3] S
F11 = east 17, south 8 -> [17, -8] S
A data structure for rotation
- As stated in the puzzle description, the ship starts facing
east- 90 degrees - The input contains two flags that change the ship's direction:
LandRfollowed by a value divisible by 90
How might I account for this scenario?
Direction = 90
L180
Direction = 270
- Subtraction won't work: I'd get -90
- Addition would work, but only coincidentally due to the half turn
What if I used an ordered array of possible degrees acting as a compass?
[90, 180, 270, 0]
With each rotational instruction, check the character used and mutate the array accordingly:
L180
L = shift values right
180 / 90 = 2
Perform 2 shift-rights
Before any:
[90, 180, 270, 0]
After 1:
[0, 90, 180, 270] -> Check first cell -> Ship facing north
After 2:
[270, 0, 90, 180] -> Check first cell -> Ship facing west
R90
R = shift values left
90 / 90 = 1
Perform 1 shift-left
Before any:
[270, 0, 90, 180]
After 1:
[0, 90, 180, 270] -> Check first cell -> Ship facing north
This feels overly complicated and has a time and space complexity that is drastically exponential.
But I think it will work.
A data structure that maps rotation to movement
- Instructions with any of
NSEWmovement seem like simple conditional clauses that never vary - However, instructions with
Fmovement depend on the direction the ship is currently facing - I have an algorithm and data structure now to track the current rotation of the ship
- I want the same two things for moving the ship along the correct axis...without requiring the same number of conditional clauses as for the other four sets of movement
Knowing I will always have one of four numbers as my current degree of rotation stored intentionally as indices in an array
[ 0, 90, 180, 270 ]
I can perform a look-up of the same index of the current degree (always the first location thanks to my algorithm above) in another array that stores modifier values by which to multiply the integer in the instruction for both axes
/*
deg : n/s e/w
*/
{
'0' : [ 1, 0],
'90' : [ 0, 1],
'180': [-1, 0],
'270': [ 0, -1]
}
How would this work?
F10
Direction = east (90)
[90, 180, 270, 0]
Current position:
[0, 0]
y x
Look-up '90' in object above:
[0, 1]
[0 + (10 * 0), 0 + (10 * 1)]
[0, 10]
n e
Altogether to form a working algorithm
Use the regular expression to generate a list containing only the two capture groups for each line from the puzzle input
Convert the second capture group's value to a number
Create the data structure and initial state of the compass: degree values for each of the four directions, starting with east
Create the data structure mapping each of the four directions to a triplet containing an ordinal direction and a pair of multiplier modifiers
For each item in the list of matched capture groups
Update a 2-element array - starting with both elements set to 0 - according to the following rules:
If the character in the first capture group is either 'L' or 'R'
Do as many times as equates to the value from the second capture group divided by 90
If the character is an 'L'
Move the number at the end of the 4-element degree array to the beginning
Else - the character is an 'R'
Move the number at the beginning of the 4-element degree array to the end
Else
If the character is either 'N','E','S','W'
Lookup and temporarily store the 3-element array value in the object mapping degrees to ordinal direction and multiplying modifiers where the ordinal direction matches the character in the first capture group
Update the 2-element array such that:
Element 1 reflects a number equivalent to: the sum of the current number and the product of the value from the second capture group and the multiplying modifier in location 2 of the 3-element array
Element 2 reflects a number equivalent to: the sum of the current number and the product of the value from the second capture group and the multiplying modifier in location 3 of the 3-element array
Else - the character is 'F'
Update the 2-element array such that:
Element 1 reflects a number equivalent to: the sum of the current number and the product of the value from the second capture group and the multiplying modifier in location 2 of the 3-element array associated with the degree key that matches the number in location 1 of the 4-element degree array
Element 2 reflects a number equivalent to: the sum of the current number and the product of the value from the second capture group and the multiplying modifier in location 3 of the 3-element array associated with the degree key that matches the number in location 1 of the 4-element degree array
Calculate the sum of the absolute values of both elements in the final state of the accumulated array
Return the sum
Building a ship voyage simulator
- It's no fun to watch a pair of coordinates update
- It's way more fun tracking the ship's location top-down along a 2D plane
- Building that experience was quite the additional puzzle
Steps taken to build the simulator
- Create a new 4-element array that would store the N,E,S,W-most coordinates reached by the ship
- Run the algorithm entirely to calculate those four numbers
- Create a 2D array as 'tall' as the range from N-S and as 'wide' as the range from W-E
Then in the main loop
For each instruction line
Store two coordinates - start and end location
Compare each X,Y coordinate in each location to determine whether the ship moved horizontally or vertically
Place an 'X' at the end location
Place an '-' or '|' at each location between the start and end location
The hardest part for me was fiddling with the math to correctly draw each bit of the trail:
- Realizing I must use absolute values when moving West
- Recognizing when to add or subtract the incrementing/decrementing value that tracked the ship's vertical or horizontal movement
- Remembering to account for the fact that the top-left point is not 0,0 - so I have to offset the north- and west- values to properly draw the place-markers
After lots of trial and error - both in the code and playing with the simulator to discover new bugs - I think it works on any input!
Here's what I saw after it ran on my puzzle input
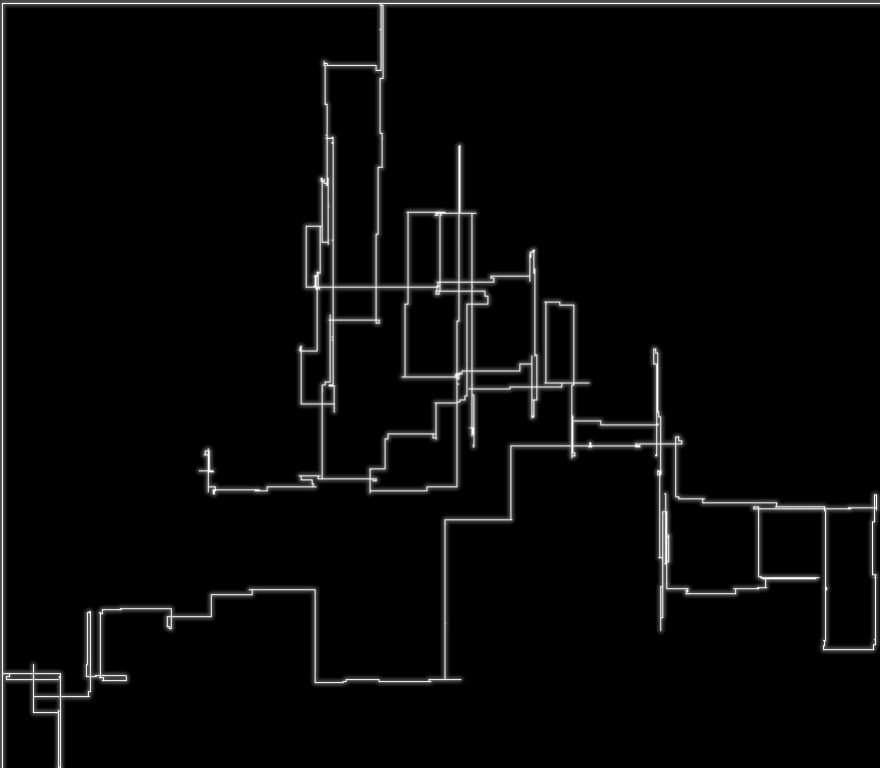
Part 2
- A new player has entered
- A small tweak to make the ship follow the waypoint
- A head-scratcher to re-orient the waypoint
- An algorithm that doesn't work
- Discovering the exact spot my algorithm breaks
A new player has entered
- This part introduces a 'carrot on a stick' element by way of a waypoint whose location must also be tracked
- It was exciting to learn how the rules and puzzle input adjusted to accommodate this
- And even more exciting to feel like I could solve it
A small tweak to make the ship follow the waypoint
- In Part 1,
Finstructions moved the ship a single integer value along one axis - In Part 2,
Finstructions move the ship along both axis the amount derived from multiplying the waypoint's coordinates by a shared integer
Ships coordinates:
[ x, y]
Waypoint's coordinates:
[ X, Y]
Instruction:
F10
N = 10
Calculation:
[ x + (N * X), y + (N * Y)]
In JavaScript, I represented that using map:
ship.map((number, index) => number + (waypoint[index] * N))
A head-scratcher to re-orient the waypoint
- In Part 1,
LandRinstructions changed the orientation of the ship - which I represented by shifting the order of degrees in an array and always referencing the first one - In Part 2,
LandRinstructions rotate the waypoint around a central point - the ship - causing the waypoint's coordinates to swap order and positivity/negativity of value
I found this diagram helpful in understanding:
|
[-y,+x] | [+x,+y]
|
--------S--------
|
[-x,-y] | [+y,-x]
|
How I thought to represent this model algorithmically:
For each rotation change
Swap the order of the waypoint's coordinates
Adjust the polarity (absolute negative value) based on the current orientation as stored in a look-up table
An algorithm that doesn't work
- Well, it works on the example input
- But not on my puzzle input
- I wanted to know why
- So, once again, I referenced JavaScript solver NullDev's solution
Discovering the exact spot my algorithm breaks
After adding some console.log() statements to both codebases and shortening the list of instructions to process until reaching the exact moment that our Manhattan Distance was different, I discovered my code's error:
- For some reason, the first
R180instruction caused my waypoint's coordinates to update incorrectly
The way my algorithm works:
pos is a function that returns the absolute value of a number
neg is a function that returns the negated absolute value of a number
quadrants is a 4-element array where each item is a 2-element array containing the correct function above that represents each rotation's correct coordinate polarity:
1. NE: [pos, pos]
2. SE: [neg, pos]
3. SW: [neg, neg]
4. NW: [pos, neg]
For each 90-degree increment of rotation in any L or R instruction
Shift the order of the elements in the array appropriately
Swap the order of the waypoint's coordinates
Apply each respective function from the now-first array element to each of the waypoint's re-ordered coordinates
- Unfortunately in the case of
R180, my algorithm incorrectly updates the waypoint's coordinates - I'm not sure how I could adjust it to work properly
- I think it is fundamentally broken
In great news, it seems NullDev shared my reasoning...albeit with a better designed algorithm.
Mixed feelings as I leave this challenge
Feeling bummed:
- I really thought my algorithm would work for part 2
Feeling great:
- I solved part 1
- I built a fun-to-watch simulator
- I attempted part 2 and got it to work for the example input
- I used another developer's code to identify a bug in mine
- I confirmed that the core of my approach to solving part 2 was spot-on...even if not executed correctly
- I learned a few better methods for calculating the current orientation and coordinates by studying NullDev's code




Top comments (0)