Monitoring Station

Advent of Code 2019 Day 10

Task: Solve for X where...

Part 1

X = the number of visible asteroids that can be detected from the asteroid where the most asteroids are visible

Part 2

X = the result of an equation leveraging the coordinates of the 200th asteroid destroyed by a laser located on the asteroid identified in Part 1

Example input

.#..#
.....
#####
....#
...##

It represents:

• A map of all the asteroids in a region of space
• .s are emptiness
• #s are asteroids (tiny ones that only occupy a small space at the center of that location)

Part 1

1. Visualizing each angle for a few points to try crafting an algorithm
2. Considering better paths that an algorithm could follow
3. A visual depiction of the algorithm I plan to build
4. A written summary of how the algorithm should work
5. Woah. That worked! I'm shocked!

Visualizing each angle for a few points to try crafting an algorithm

Here's the example input again:

.#..#
.....
#####
....#
...##

I'll use the center asteroid in the example input map region:

  # 

The eight easy lines of sight to check are horizontal, vertical and diagonals:

\ | /
 812
-7#3-
 654
/ | \

Using center as (0,0):

• 1 is at angle (-1, 0)
• 2 is at angle (-1, 1)
• 3 is at angle ( 0, 1)
• 4 is at angle ( 1, 1)
• 5 is at angle ( 1, 0)
• 6 is at angle ( 1,-1)
• 7 is at angle ( 0,-1)
• 8 is at angle (-1,-1)

But how would I get each of the other 352 angles?
Or, well, other 8 angles in this example?

 8 1
7   2
  #
6   3
 5 4

Using center as (0,0):

• 1 is at angle (-2, 1)
• 2 is at angle (-1, 2)
• 3 is at angle ( 1, 2)
• 4 is at angle ( 2, 1)
• 5 is at angle ( 2,-1)
• 6 is at angle ( 1,-2)
• 7 is at angle (-1,-2)
• 8 is at angle (-2,-1)

Do I notice any patterns?

• The range for X,Y values spans the boundaries of the region: from (0,0) it's (-2 to 2, -2 to 2)

Here's the example input again:

.#..#
.....
#####
....#
...##

Now, I'll use the winning asteroid in the example input map region:

.....
.....
.....
.....
...#.

The direct lines to check are:
First angle: (-1,0) until an asteroid is spotted or the region boundary is exceeded

• Check (-1,0): empty
• Check (-2,0): hit! stop

Next angle: (-4,1)...

• Check (-4,1): hit! stop

Next angle: (-3,1)...

• Check (-3,1): empty
• Check (-6,2): out of range! stop

Next angle: (-2,1)...

• Check (-2,1): hit! stop

Next angle: (-1,1)...

• Check (-1,1): hit! stop

Next angle: ( 0,1)...

• Check (0,1): hit! stop

Somehow skip to degrees 90 - 269.

Next angle: (0,-1)...

• Check (0,-1): empty
• Check (0,-2): empty
• Check (0,-3): empty
• Check (0,-4): out of range! stop

Next angle: (-1, -3)...

• Check (-1, -3): empty
• Check (-2, -6): out of range! stop

Next angle: (-1, -2)...

• Check (-1, -2): empty
• Check (-2, -4): out of range! stop

Next angle: (-1, -1)...

• Check (-1, -1): empty
• Check (-2, -2): hit! stop

Next angle: (-2, -1)...

• Check (-2, -1): hit! stop

Next angle: (-3, -1)...

• Check (-3, -1): empty
• Check (-6, -2): out of range! stop

Next angle: (-4, -1)...

• Check (-4, -1): empty
• Check (-8, -2): out of range! stop

Wait, that's only 7 hits. There should be 8. What did I miss?

.....
.....
*....
.....
...S.

That is at angle: (-2, -3)
How could I have targeted that?

• Not via any (-1,x) path
• Only via the (-2,x) path

But from (-2,-1) there's:

• (-2,-2), which has already been checked

I guess I could have just kept going until out of range:

• (-2,-3): hasn't been checked, is a hit!

So, what might my path have been?

Part 1
....3
....4
...25
...16
...#7

Part 2
....x
....x
.7.xx
456xx
321#x

Part 3
987.x
654.x
321xx
xxxxx
xxx#x

That seems like a custom path, not one followed by some consistently incrementing or decrementing X,Y relative coordinates.

Considering better paths that an algorithm could follow

The example input, again:

.#..#
.....
#####
....#
...##

From the middle point, four paths that start from each diagonal and continue toward a border:

^^ ->
|| ->
  #
<- ||
<- vv

Followed by checks of the horizontal and vertical lines of sight:

  ^  
  |  
<-#->
  |  
  v  

Altogether forming this pattern:

^^^->
|||->
<-#->
<-|||
<-vvv

Or, following concentric circles:

First pass

\ | /
 812
-7#3-
 654
/ | \

Next pass

.8.1.
7...2
..#..
6...3
.5.4.

Yikes. This feels overly complicated.

But I've got to try building it!

A visual depiction of the algorithm I plan to build

This demonstrates how the algorithm I plan to build should work:

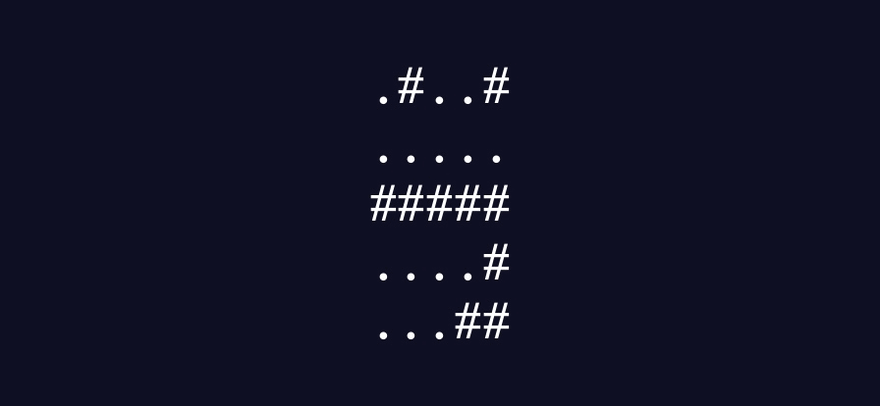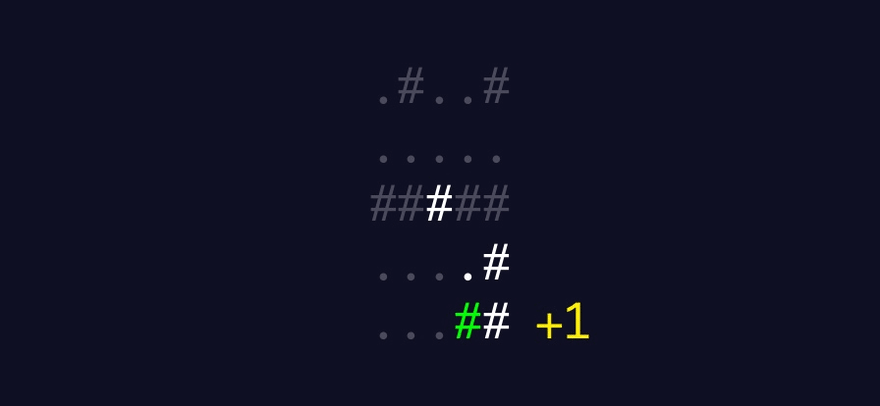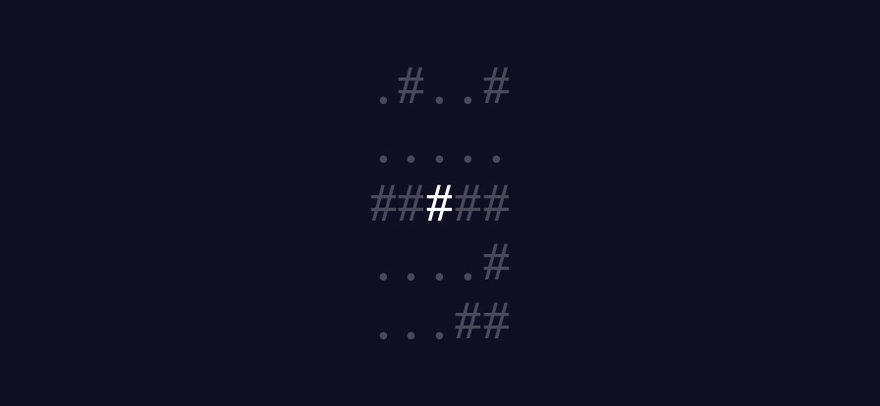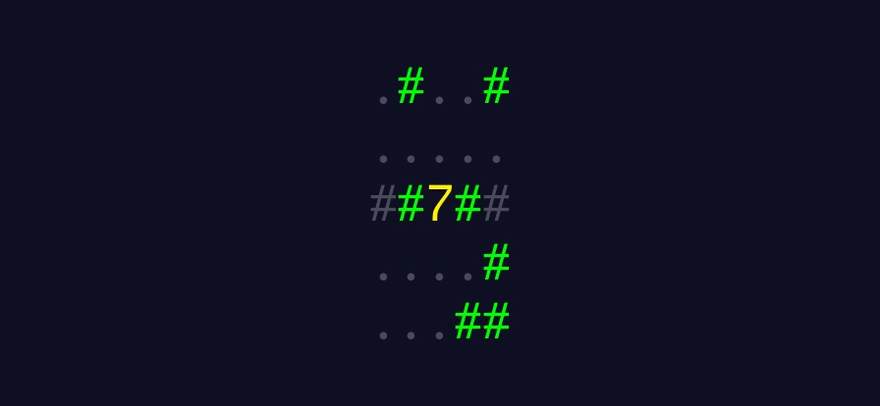
A written summary of how the algorithm should work

For each value in the region map that contains an asteroid

Perform two rounds: one starting from each immediate diagonal coordinate, and another from each horizontally- and vertically-adjacent coordinate

Round 1
For each of the four immediately diagonal coordinates
  Visit every cell in that quadrant bordered by the x- and y-axes
  Track the tally of asteroids spotted, starting at 0
  Track a unique set of values representing coordinates of each visited cell
  From each initial cell
    Track how many asteroids were spotted via a list of boolean values
    Do as long as the cell exists in the map region
      As long as the cell hasn't been visited yet
        If it is an asteroid, add True to the list of spotted asteroids
        Else, add False to the list
      Add it to the list of visited cells
      Move a distance equal to the relative distance between the originating coordinate and the initial cell's coordinates
    If there is at least one True value in the list of spotted asteroids, increment the tally by 1
  Return the tally
Return the sum of all four tallies

Round 2
For each of the four horizontally- and vertically-adjacent coordinates
  Track the tally of asteroids spotted, starting at 0
  Do as long as the cell exists in the map region
    If the cell's value is an asteroid
      Increment the tally by 1
      Break
    Else, move one step in the current direction (up, right, down or left)
  Return the tally
Return the sum of all four tallies

Return the sum of each sum of tallies

Return the largest sum from the new list of summed tallies

Woah. That worked! I'm shocked!

• I ran it on each example
• Each time it generated the correct answer
• I ran it on my puzzle input
• And it, too, generated the correct answer!

Part 2

1. Yikes! Order matters now.
2. Throwing in the towel

Yikes! Order matters now.

• We're still counting...
• But from a specific angle...
• In a specific direction...
• So the order of asteroid detection is important

Throwing in the towel

I can't think of an algorithmic way to re-create a pathfinding algorithm akin to the abstract laser rotating in this puzzle.

So, sadly, Part 2 will go unsolved.

Celebrating my accomplishments

• I solved Part 1! I really didn't think I would.
• I made a cool GIF that accurately visualized my peculiar algorithm

Bummer:

• No simulator...mostly because it didn't seem worth it
• No correct answer for Part 2...though I'm content with solving Part 1

Today's puzzle was a wonderful twist on the recurring 'find adjacent things' theme.

And I'm so delighted I solved Part 1.