Advent of Code 2018 Day 23
Task: Solve for X where...
Part 1
X = the number of nanobots in range of the nanobot with the largest signal radius
Example input
pos=<0,0,0>, r=4
pos=<1,0,0>, r=1
pos=<4,0,0>, r=3
pos=<0,2,0>, r=1
pos=<0,5,0>, r=3
pos=<0,0,3>, r=1
pos=<1,1,1>, r=1
pos=<1,1,2>, r=1
pos=<1,3,1>, r=1
It represents:
- A list of several tiny nanobots' position and signal radius
- Position is in three axes:
X,Y,Z
Part 1
- Seems easy given I solved Day 25 Part 1
- A regular expression to parse each position and signal radius
- A written description of my working algorithm
Seems easy given I solved Day 25 Part 1
- That puzzle also required computing the Manhattan Distance of a series of integers among objects
- It featured four
dimensions, whereas this puzzle features three - It required multiple iterations to compare each object to all objects after it, whereas for this task I just have to find a maximum value and compare all objects to an identified individual
A regular expression to parse each position and signal radius
A string I'll have to parse is:
pos=<1,0,0>, r=1
Initial impression leads me to this regular expression:
/pos=<\d+,\d+,\d+>, r=\d+/g
I'll use regexr.com to troubleshoot.
- I was forgetting that each position could also be negative.
- I needed capture groups.
- I could consolidate each of the first groups into one.
Here's the updated regular expression:
pos=<(-?\d+,?)+>, r=(\d+)
Wait a minute. Why am I over-complicating this?
/-?\d+/g
- This will find all occurrences of negative or positive integers, of which I know there will always be 4
That's all I needed!
A written description of my working algorithm
Split the input at each newline character into an array of strings
Change each string into an array of four integers resulting from using the regular expression to extract each integer
To find the nanobot with the strongest signal:
Find the largest integer among the integers in the last location of the four-integer array
Find the index of the array where that number was found in the last location
Store the array at that index as strongest
To find all nanobots in range of the strongest nanobot:
For each nanobot, accumulate a value - starting at 0
Calculate the sum of the absolute values of the differences of the integers in positions x,y,z in the strongest nanobot and the current nanobot
Increment the accumulating tally by one if the sum is less than or equal to the strongest nanobot's signal
Otherwise, don't increment the tally
Return the accumulated tally
A visual depiction of my working algorithm
Part 2
Yikes! The spectrum of values that need consideration seems unbounded!
I honestly wouldn't know where to begin to solve this part.
Sadly, I won't be giving this part more consideration than the initial read-through.
Celebrating my accomplishments
- I solved Part 1!
- I made a GIF of my algorithm
Bummers:
- No simulator
- I didn't even try to attempt Part 2 given its seemingly broad scope


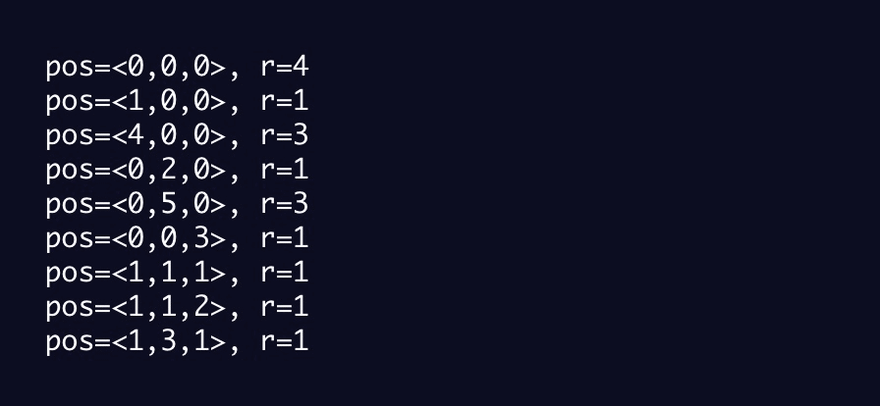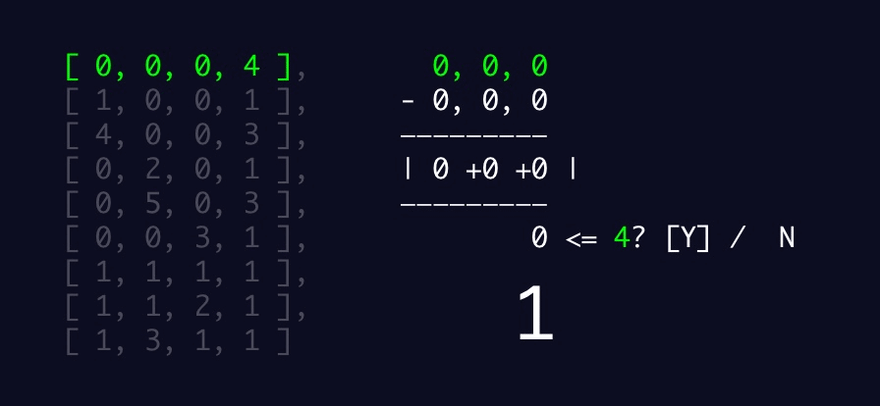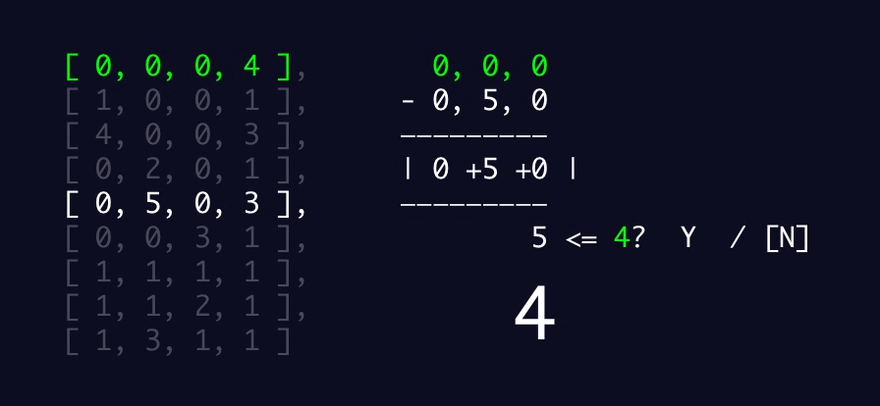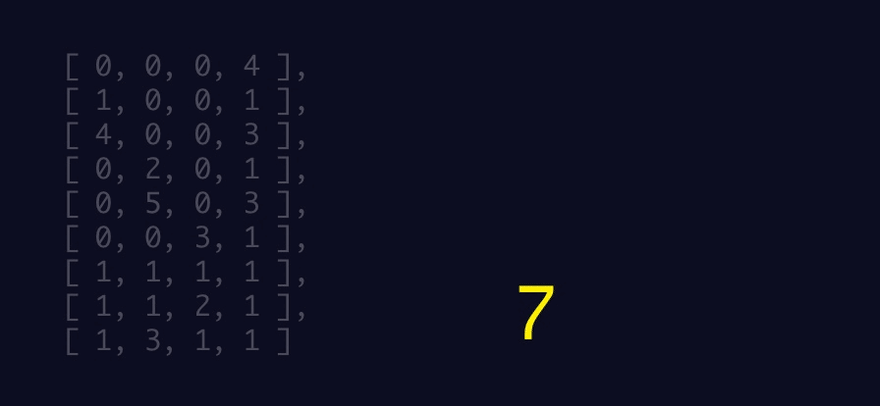

Top comments (0)