Advent of Code 2017 Day 24
Part 1
- Recognizing the task
- Understanding the language of the puzzle
- Analyzing the example input
- Imagining an algorithm based on the example breakdown
- First attempt: flat-out failure
- Second attempt: shocking success!
Recognizing the task
Abstractly, the task is to:
Build a bridge out of the magnetic components strewn about nearby
The initial task is to:
Solve for X such that X =...
the strength of the strongest bridge I can make with the components I have available
Understanding the language of the puzzle
- A bridge is formed using components
- Each component is comprised of two ports
- Each port is identified by the number of pins it uses
- Components can only connect thru identically-numbered port ends
- Components can connect to either end of the component...not just left-to-right or right-to-left ends as depicted in the input
- The higher the port number, the stronger the bridge
- The first component must feature one zero-pin port
- It doesn't matter how many pins are in the ending port
Analyzing the example input
The example puzzle input:
0/2
2/2
2/3
3/4
3/5
0/1
10/1
9/10
- It is a list of components
- Each one designating the pins in each of its two ports
- There are only a few components that could act as the first one
- There is one component whose ports have the same number of pins
Imagining an algorithm based on the example breakdown
The list of bridges is depicted as:
0/1
0/1--10/1
0/1--10/1--9/10
0/2
0/2--2/3
0/2--2/3--3/4
0/2--2/3--3/5
0/2--2/2
0/2--2/2--2/3
0/2--2/2--2/3--3/4
0/2--2/2--2/3--3/5
If manipulated, it would resemble a tree, with two root nodes:
0/1
10/1
9/10
0/2
2/3
3/4
3/5
2/2
2/3
3/4
3/5
Interesting. How might I re-create this data structure?
Likely using:
- Recursion
- Ordered lists where each item is a unique two element list
- Maybe
flatMap()to generate sub-lists and eventually combine them into a flattened array?
This animation illustrates one approach:

This task seems doable.
I need to carefully consider how my algorithm and initial data structure should work.
First attempt: flat-out failure
I tried re-creating the first and second steps of the example input:
- Find all zero-pin port-containing components
- Find each next possible set of components
Step 1 was easy:
- Filter the list of components to only the ones including a 0
Step 2 tripped me up:
- My filter was only finding one of the two remaining two-pin port components
I had no idea what I was doing wrong.
Time to step away, think on things, and return later.
Second attempt: shocking success!
- My original GIF implies that I need to ultimately compare and merge leaf-node arrays all the way back up the tree to the root nodes
- That seemed tricky...like it was going to require a lot of extra code and headache
While walking my dog, I had a realization:
- Once I get to a leaf node, I know I've found the last possible component for the current bridge
- As long as I've been accumulating all prior components up to that point, I can calculate the strength of that bridge in the base case of the leaf node
- If the strength is greater than the current value stored in strength (updated in one of the other many recursive calls), update strength to the new greatest value
- At the end, return the current value in strength, which should reflect the strongest bridge
My recursive algorithm works like this:

What I saw as my algorithm ran Part 1:

Part 2
- Recognizing the new task
- Part 1, but with a more complex comparison
Recognizing the new task
Solve for X such that X =...
the strength of the longest bridge I can make with the components I have available
Part 1, but with a more complex comparison
- In Part 1, I tracked and compared only a strength
- Now, I need to track and compare a length and a strength
If at a leaf node
If the length of the accumulated bridge components is greater than the current winner
Update the winner to reflect this bridge's length and strength
Else, if the lengths of the current winner and this bridge are equal
Update the winner to reflect the length and strength of the stronger bridge
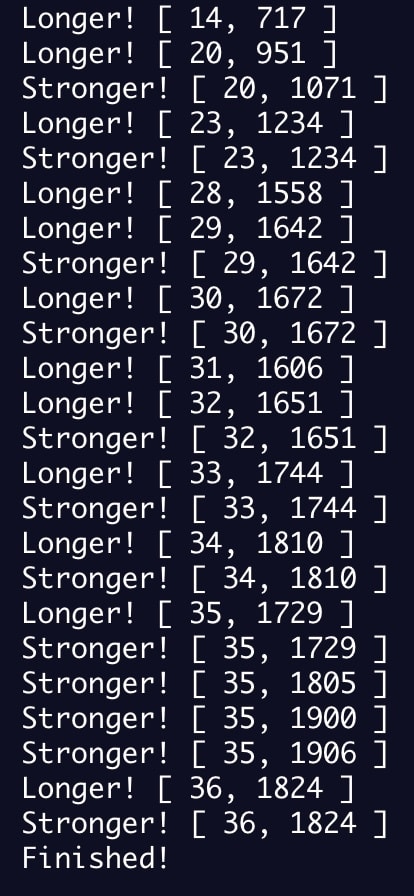
What I saw as my algorithm ran Part 2:
I did it!!
- I solved both parts!...
- ...of a recursive algorithm puzzle!
- I got two gold stars for the second time on a Day 24!
- I made two GIFs: one depicting my initial, naive algorithm, and another outlining my refined, working algorithm
Any time I solve both parts of a puzzle after Day 15 calls for celebration!



Top comments (0)