2021/01/05 - The previous C# code sample implemented the algorithm incorrectly. A corrected Java implementation has been added in its place.
If you are unfamiliar with graphs, check out some of my earlier posts on them.
Resources:
Takeaways:
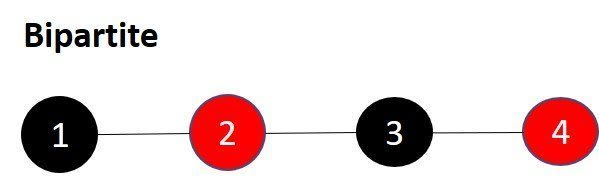
- A bipartite graph (bigraph) is a graph where the vertices can be divided into two disjoint, independent, sets
uandv. Every edge will connect a vertex from one set to the other (without self referencing edges - I.E edges going from a vertex inuto another vertex inu). - One way to visualize a bipartite graph, is to colour all the vertices in a set the same colour. Set
ucould be red vertices, whereasvcould be black. This would mean an edge would always consist of a red and black pair of vertices. - This type of two-colouring is impossible in non-bipartite graphs. Think of a graph with three vertices arranged in a triangle. We cannot represent this graph as two independent sets, and we cannot two-colour it in such a way that will allow each edge to have different coloured endpoints.
- One way in which we can check if a graph is bipartite, is to run a depth-first search (DFS) over the vertices. Applying two colouring to the graph.
- Start at a random vertex
vand colour it colour1 (red, for example). - Colour all adjacent vertices
uthe opposite colour ofv. For each adjacentu, also recursively call our DFS routine. - If a graph is bipartite, we can complete this two-colouring without a contradiction.
- If the graph is not bipartite, then at some point a vertex will get both colours - and this contradiction means we cannot achieve a two-colouring of the graph.
- Start at a random vertex
- Time complexity is
O(v + e)for an adjacency list. Space complexity isO(v). For an adjacency matrix, the time & space complexity would beO(v^2).
Undirected graph that can be two-coloured:
Undirected graph that cannot be two-coloured:

Below are implementations for checking if undirected graphs are bipartite. There is solutions for both undirected adjacency list & adjacency matrix representations of graphs:
As always, if you found any errors in this post please let me know!


Top comments (0)