If you are unfamiliar with graphs, check out some of my earlier posts on them.
Resources:
Takeaways:
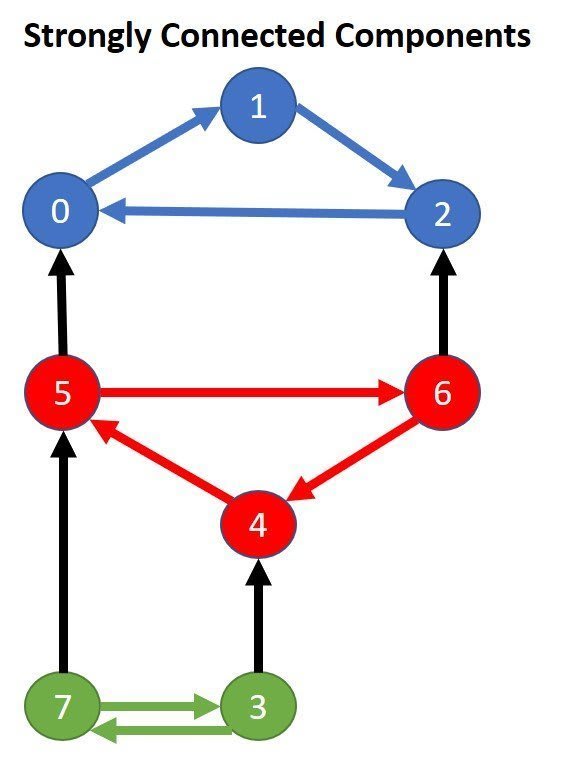
- A strongly connected component in a directed graph is a partition or sub-graph where each vertex of the component is reachable from every other vertex in the component.
- Strongly connected components are always the maximal sub-graph, meaning none of their vertices are part of another strongly connected component.
- Finding strongly connected components is very similar to finding articulation points & bridges. Many of the solutions for finding them involve depth-first search (DFS).
- One way to find strongly connected components is using Tarjan's Algorithm.
- Tarjan's Algorithm uses DFS and a stack to find strongly connected components.
- The algorithm overview is:
- For every unvisited vertex
vin the graph, perform DFS. - At the start of each DFS routine, mark the current vertex
vas visited, pushvonto the stack, and assignvan ID and low-link value. - Initially, like with articulation points & bridges, the ID and low-link values of
vwill be the same. - Increment the integer value we are using as the ID/low-link seed. So the next vertex
wto enter our DFS routine will get a higher value for both (compared tov). - For every adjacent vertex
uofv, ifuis unvisited, perform DFS (recursive call). - On exit of the recursive DFS call, or if
uhad already been visited, check ifuis on the stack. - If
uis on the stack, update the low-link value ofvto be smallest betweenlow-link[v]andlow-link[u]- low-link represents the earliest ancestor of a vertex (a lower value means the vertex entered DFS earlier). In other words, low-link is the ID of the earliest vertex
yvertexvis connected to.
- low-link represents the earliest ancestor of a vertex (a lower value means the vertex entered DFS earlier). In other words, low-link is the ID of the earliest vertex
- After exploring all adjacent vertices of
vcheck if the ID ofvis the same as it's low-link value - If they are the same, then
vis the root of a strongly connected component. - If they are the same, pop all vertices off the stack up to and including
v. All of these vertices represent a single strongly connected component - Complete the above steps for the entire graph, and all strongly connected components will be discovered.
- For every unvisited vertex
- Time complexity of Tarjan's Algorithm is
O(v + e)- wherevis the number of vertices, andethe number of edges, in a graph. - Space is
O(v)
Below are implementations for finding strongly connected components in undirected adjacency list & adjacency matrix representations of graphs:
As always, if you found any errors in this post please let me know!


Top comments (0)