Resources:
- Video on detecting cycles in directed graphs
- Video on detecting cycles in undirected graphs
- MIT video on detecting cycles in graphs
- Helpful implementation for detecting cycles in adjacency matrix
- Deadlock Detection in the book: Elements of Programming Interviews
To get the most out of this article, it is helpful if you already know what a graph is, and ideally what depth-first search is. A previous post of mine covers the basics of graphs and graph traversals.
Some takeaways:
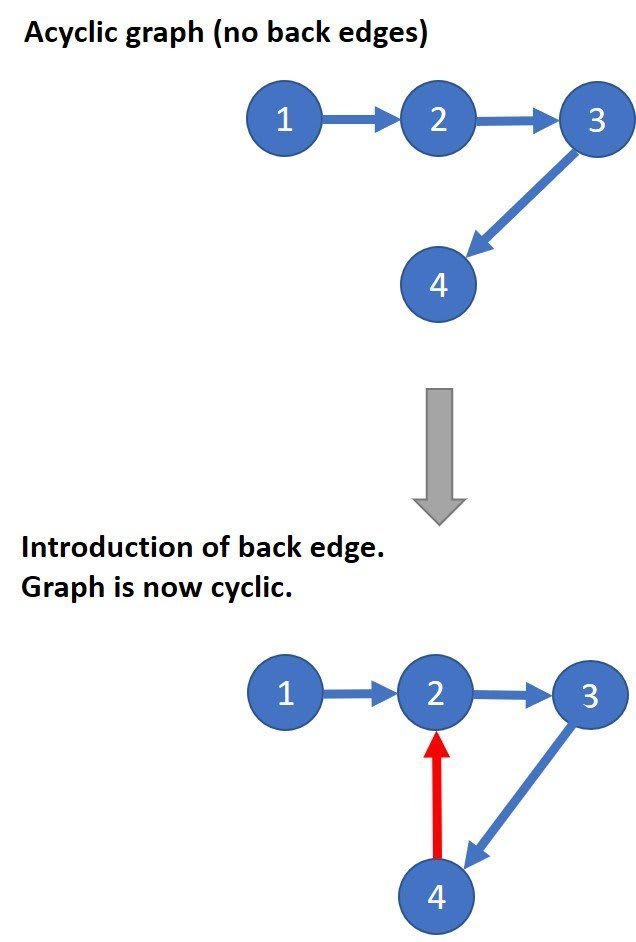
- A graph cycle is when there is a "loop" or circular reference. This can be a series of edges that connect back to an origin vertex.
- If a graph has a cycle it is a cyclic graph.
- To determine if a graph has a cycle, we can traverse the graph and look for a back edge.
- A back edge is one that connects a vertex to an already visited ancestor.
- Example:
- To detect a cycle in a directed graph (i.e to find a back edge), you can use depth-first search (with some introduction of local state to tell you if a back edge occurs):
- We will maintain 3 buckets of vertices: white, grey, & black buckets. (We can also colour vertices instead).
- The white bucket will contain all of the unvisited vertices. At the start of our traversal, this means every vertex is in the white bucket.
- Before visiting a vertex, we will move it from the white bucket into the grey bucket.
- After fully visiting a vertex, it will get moved from the grey bucket into the black bucket.
- We can skip over vertices already in the black bucket, if we happen to try and visit them again.
- When visiting the children/descendants of a vertex, if we come to a descendant vertex that is already in the grey bucket - that means we have found a back edge/cycle.
- This means the current vertex has a back edge to it's ancestor - as we only arrived at the current vertex via it's ancestor. So we have just determined that there is more than one path between the two (a cycle).
- We will maintain 3 buckets of vertices: white, grey, & black buckets. (We can also colour vertices instead).
- To detect a cycle in an undirected graph, it is very similar to the approach for a directed graph. However, there are some key differences:
- We no longer colour vertices/maintain buckets.
- We have to make sure to account for the fact that edges are bidirectional - so an edge to an ancestor is allowed, if that ancestor is the parent vertex.
- We only keep track of visited vertices (similar to the grey bucket).
- When exploring/visiting all descendants of a vertex, if we come across a vertex that has already been visited then we have detected a cycle.
- Time complexity is
O(v + e)for an adjacency list. Space complexity isO(v). For an adjacency matrix, the time & space complexity would beO(v^2).
Although using depth-first search is common for cycle detection, you can also detect cycles using topological sort too. I have yet to cover topological sorting of graphs - but will be doing so in a later post.
Below are implementations of cycle detection via depth-first search in both undirected & directed graphs. I have implemented each for an adjacency list (Graph) & an adjacency matrix (Graph2):
As always, if you found any errors in this post please let me know!


Top comments (0)