This is part of a series of Leetcode solution explanations (index). If you liked this solution or found it useful, please like this post and/or upvote my solution post on Leetcode's forums.
Leetcode Problem #1738 (Medium): Find Kth Largest XOR Coordinate Value
Description:
You are given a 2D matrix of size m x n, consisting of non-negative integers. You are also given an integer k.
The value of coordinate (a, b) of the matrix is the XOR of all matrix[i][j] where 0 <= i <= a < m and 0 <= j <= b < n (0-indexed).
Find the kth largest value (1-indexed) of all the coordinates of matrix.
Examples:
| Example 1: | |
|---|---|
| Input: | matrix = [[5,2],[1,6]], k = 1 |
| Output: | 7 |
| Explanation: | The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value. |
| Example 2: | |
|---|---|
| Input: | matrix = [[5,2],[1,6]], k = 2 |
| Output: | 5 |
| Explanation: | The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value. |
| Example 3: | |
|---|---|
| Input: | matrix = [[5,2],[1,6]], k = 3 |
| Output: | 4 |
| Explanation: | The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value. |
| Example 4: | |
|---|---|
| Input: | matrix = [[5,2],[1,6]], k = 4 |
| Output: | 0 |
| Explanation: | The value of coordinate (1,1) is 5 XOR 2 XOR 1 XOR 6 = 0, which is the 4th largest value. |
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10000 <= matrix[i][j] <= 1061 <= k <= m * n
Idea:
Solving this problem with no regard for time complexity would be a simple matter, which means that the main issue is going to be finding a shortcut to not having to do the long calculations for each iteration. Since each new value that we're asked to find contains as a subset a value we've already found, it naturally brings to mind a dynamic programming solution.
First, each cell in our matrix M will have its own value, so DP will have to have the same dimensions as M. Next, let's say we're trying to find the value for X = DP[4][6]. From the instructions we know that it will be equal to each cell in the shaded area bitwise XOR'd together:
Since our DP matrix is being built top-to-bottom and left-to-right, we can get close to the necessary value with either A = DP[3][6] or B = DP[4][5]:
But even those shortcuts would allow the time complexity to increase exponentially with the size of M, since we'd still have to iterate through a whole row or column to get the other values we need for X. We could get even closer if we use both A and B, but they overlap quite a bit.
This is where it's important to realize that the bitwise XOR operation is its own inverse function:
if: x ^ y = z
⇒: z ^ y = x
⇒: x ^ y ^ y = x
This means that the overlapping sections of A and B would effectively cancel each other out, as those numbers would be XOR'd twice each:
This opens up the immediate possibility of using a third DP value (C = DP[4][4]) in conjunction with A and B to leave us only one cell away from the value of X. That means that we can find out the DP value of each new cell by combing only four other cell values:
At that point, we only need to account for i = 0 and j = 0 values to complete our DP matrix. Since we won't need any previous original cell values in order to complete the DP matrix, we can also solve the DP matrix in-place.
The final step for this problem is to then sort the values in the DP matrix in order to find the Kth highest value. Normally, this would call for a max-heap implementation, as the numbers can be readily inserted into the heap as M is being rewritten.
For Javascript, however, we can achieve a much faster sort through a typed array .sort() than we can with a max-heap implementation. (Note: I've included a version of the code with a max-heap implementation below, for comparison.)
Since the original cell values of M are limited to 1e6, which is a 20-bit binary number, the DP values are therefore limited to between 0 and 2^20 - 1. This means that we can use a Uint32Array to store the values more efficiently.
After a basic sort, we can return the Kth highest value.
Javascript Code:
var kthLargestValue = function(M, K) {
let y = M.length, x = M[0].length, ans = new Uint32Array(x*y), h = 0
for (let i = 0; i < y; i++)
for (let j = 0; j < x; j++) {
let cell = M[i][j]
if (i > 0) cell ^= M[i-1][j]
if (j > 0) cell ^= M[i][j-1]
if (i > 0 && j > 0) cell ^= M[i-1][j-1]
ans[h++] = M[i][j] = cell
}
return ans.sort()[x*y-K]
};
Javascript Code w/ Max-Heap:
var kthLargestValue = function(M, K) {
let y = M.length, x = M[0].length,
heap = new Uint32Array(x*y), hix = 0
const heapify = num => {
heap[hix] = num
let i = hix++, par = (i - 1) >> 1
while (heap[par] < heap[i]) {
[heap[par],heap[i]] = [heap[i],heap[par]]
i = par, par = (i - 1) >> 1
}
}
const extract = () => {
let max = heap[0], left, right
heap[0] = heap[--hix], heap[hix] = 0
let i = 0, child = heap[2] > heap[1] ? 2 : 1
while (heap[i] < heap[child]) {
[heap[i],heap[child]] = [heap[child],heap[i]]
i = child, left = (i + 1) << 1, right = left - 1
child = heap[right] > heap[left] ? right : left
}
return max
}
for (let i = 0; i < y; i++)
for (let j = 0; j < x; j++) {
let cell = M[i][j]
if (i > 0) cell ^= M[i-1][j]
if (j > 0) cell ^= M[i][j-1]
if (i > 0 && j > 0) cell ^= M[i-1][j-1]
heapify(M[i][j] = cell)
}
for (let i = K-1; i; i--) extract()
return extract()
};


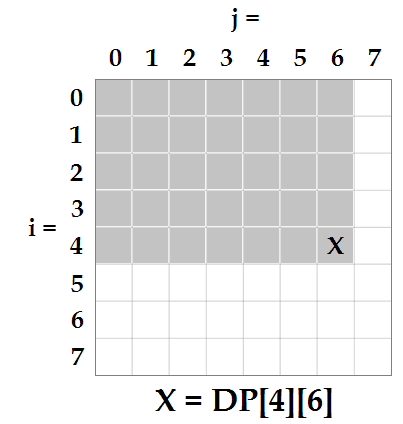




Top comments (0)