Throughout the course of this series, we’ve been learning time and again that distributed systems are hard. When faced with hard problems, what’s one do to? Well, as we learned in part one of this post, sometimes the answer is to strip away the complicated parts of a problem and try to make sense of things simply, instead.
This is exactly what Leslie Lamport did when he approached the problem of synchronizing time across different processes and clocks. As we learned in part one, he wrote a famous paper called “Time, Clocks, and the Ordering of Events in a Distributed System”, which detailed something called a logical clock, or a kind of counter to help keep track of events in a system. These clock counters were Lamport’s invention (and solution!) to the problem of keeping track of causally-ordered events within a system. By using a logical clock, we can more easily create a chain of events between processes in a system.
But how do these clocks actually work? And how does a clock actually figure out the time of events — especially when there are events happening all over the system? It’s time to finally find out.
From clock to timestamp
As we already know, logical clocks, also sometimes called Lamport timestamps , are counters. But how do those counters work under the hood? The answer may be surprisingly simple: the clocks are functions, and its the function that does the work of “counting” for us!

We can think of logical clocks as functions , which take in an event as their input, and returns a timestamp , which acts as the “counter”. Each node — which is often just a process — in a distributed system has its own local clock, and each process needs to have its own logical clock.

If we imagine the logical clock as a function that we might implement, we can think through how it works. If we were to pseudo-code that function, we could be sure that it would take an event as its argument. We will recall that an event can be something that occurs within a process, a send event that marks the process sending a message elsewhere, or a receive event that marks the process receiving an event from elsewhere. A logicalClock function should be able to take in any of these three types of events.
Once the logicalClock function has an event, it looks at the time on that event, and compares it to the time on the clock’s process. Once it compares the two, it chooses the larger of the options, and increments it arbitrarily. The increment step is important, because with logical clocks, time continues to march forward, and the increment step is what ensures that the timestamp returned by the function is always larger in value than the event’s time.
If this seems confusing, fear not! While pseudo-code can be helpful sometimes, but an example is even better. Now that we understand some of theory behind how a logical clock might work, let’s take a deeper look at how the clock algorithm _actually _works.
Lamport’s clock algorithm
In many cases, Lamport’s algorithm for determining the time of an event can be very straightforward. If an event occurs on a single process, then we intuitively can guess that the timestamp of the event will be greater than the event before it, and that the difference between the timestamps of the two events on the same process will depend only on how much the clock increments by (remember, that incrementation can be totally arbitrary!).
However, things aren’t so simple when dealing with send and receive events, which are signals that two processes are passing messages back and forth. Consider the illustration shown here, where we have two processes, P and Q. Process P has an event on the process itself: P1. The time at P1 is 2. Process Q also has an event of its own, Q1, which has a time of 2. The next event on process Q is Q2, which is a send event and marks a message being sent from process Q to process P.
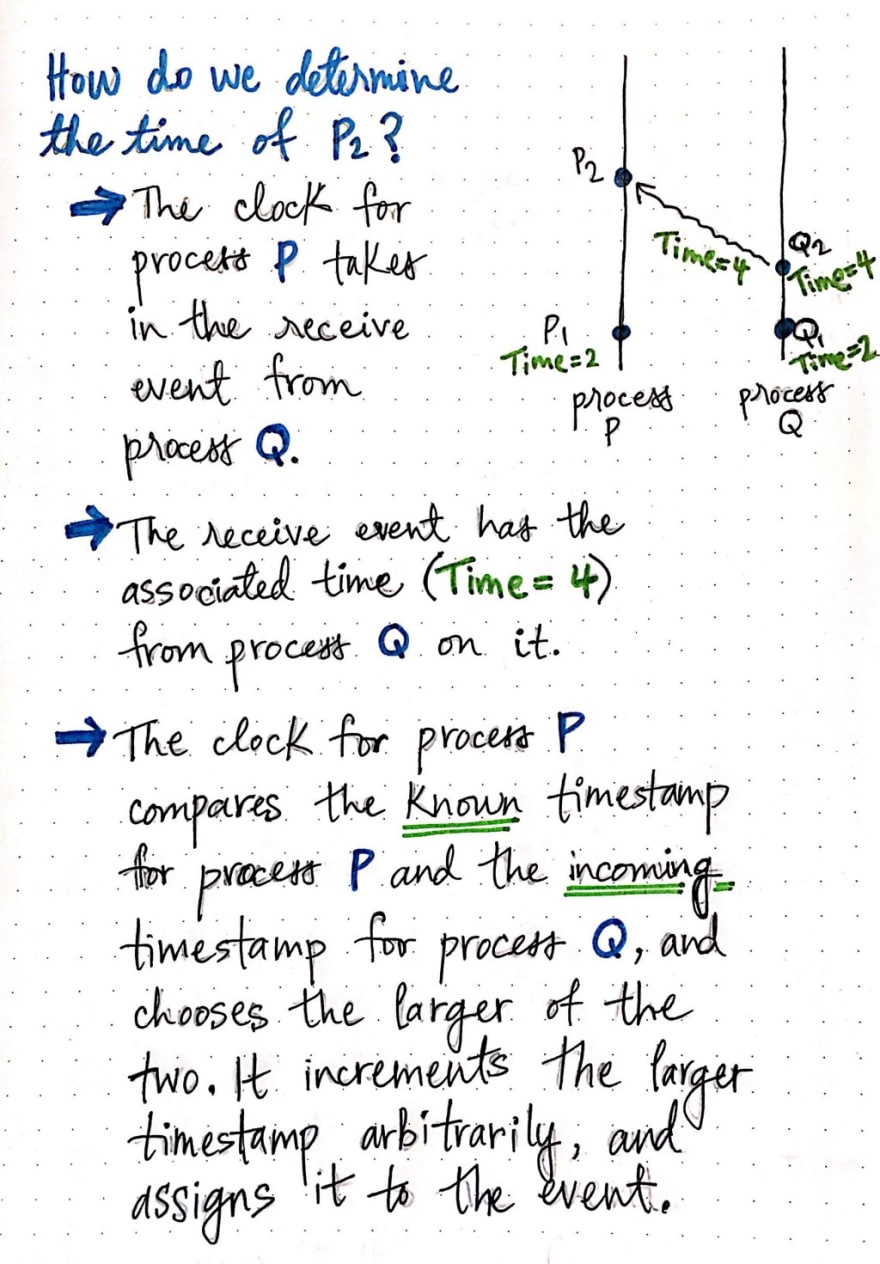
So what happens when the send event from process Q, or Q2, sends its message over to process P? Well, for one thing, when process Q sends its message to process P, it also sends the time at that particular moment along with its message. In the case of this example, the time at Q2 was 4, so the message sends time = 4, as part of its message data.
Once process P receives that message, it marks it with a receive event, or P2. Then, its logical clock looks at the incoming time on the event, and compares it to the currently-known time on its own process, process P. When it does this comparison, it chooses the larger of the two timestamps, and increments it arbitrarily.
Process P's clock sees that its currently-known time is 2, while the time on the incoming event is 4. The clock chooses the larger time between the two timestamps (4), increments it, and assigns the new timestamp to the receive event, P2. In more concrete terms, we can say that the clock uses an algorithm to do this, which can effectively be summarized as: max(processT, incomingT) + amount.
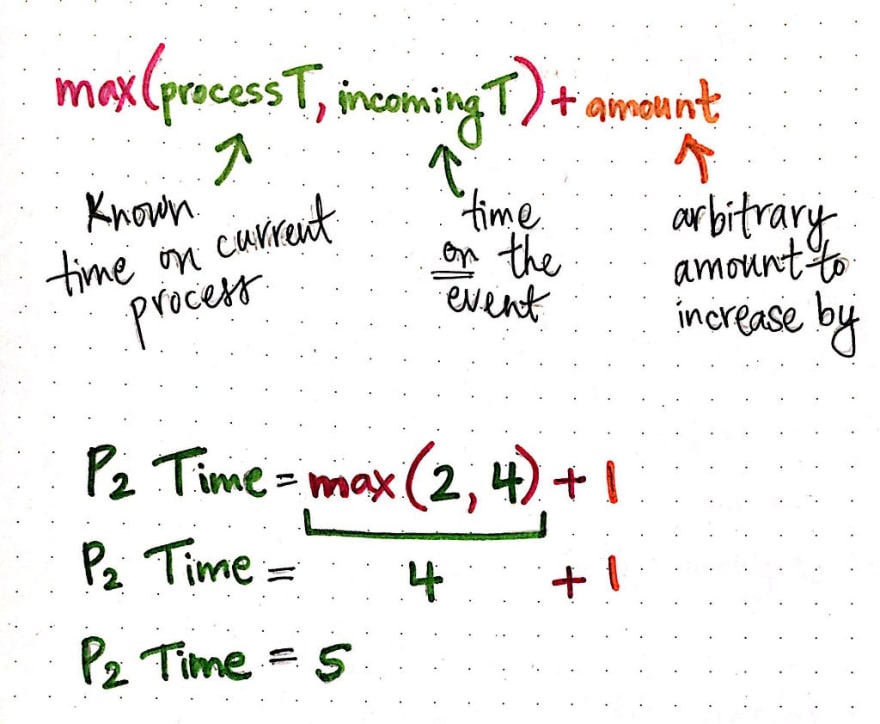
In this formula, processT is the currently-known time on the current process, while incomingT is the time on the event that the process is trying to reconcile. The clock takes the max() of that, and increments it by whatever arbitrary amount the clock is using to act as a counter and ensure that the all timestamps continue to increase in value.
In our example system, we can determine that P2’s timestamp will be the result of max(2, 4) + amount; for simplicity’s sake, we can decide to make amount equal to 1, so the time at P2 is 4 + 1 = 5.

Awesome! Our logical clock is actually doing some interesting and useful work for us, and it’s doing it in a pretty elegant and simple way.
Clocks and causality
Now that we’ve seen how clocks derive and deliver a time to us, let’s investigate when they’re useful, as well as how they’re sometimes limiting. As we already know from part one of this series, Lamport introduced the concept of happens before (using the → shorthand) to indicate that one event happens before another in a system. Understanding the chain of events in a system helps us causally order them and figure out how one event causes another to happen.
Conveniently, logical clocks obey the rules of causality. This means that if we find a causal, happens before relationship in a system, then the timestamps corresponding to these two events should obey the rules of causality.
If event a → b, then the timestamp returned by clock(a) should be less than (<) that of the timestamp returned by clock(b).
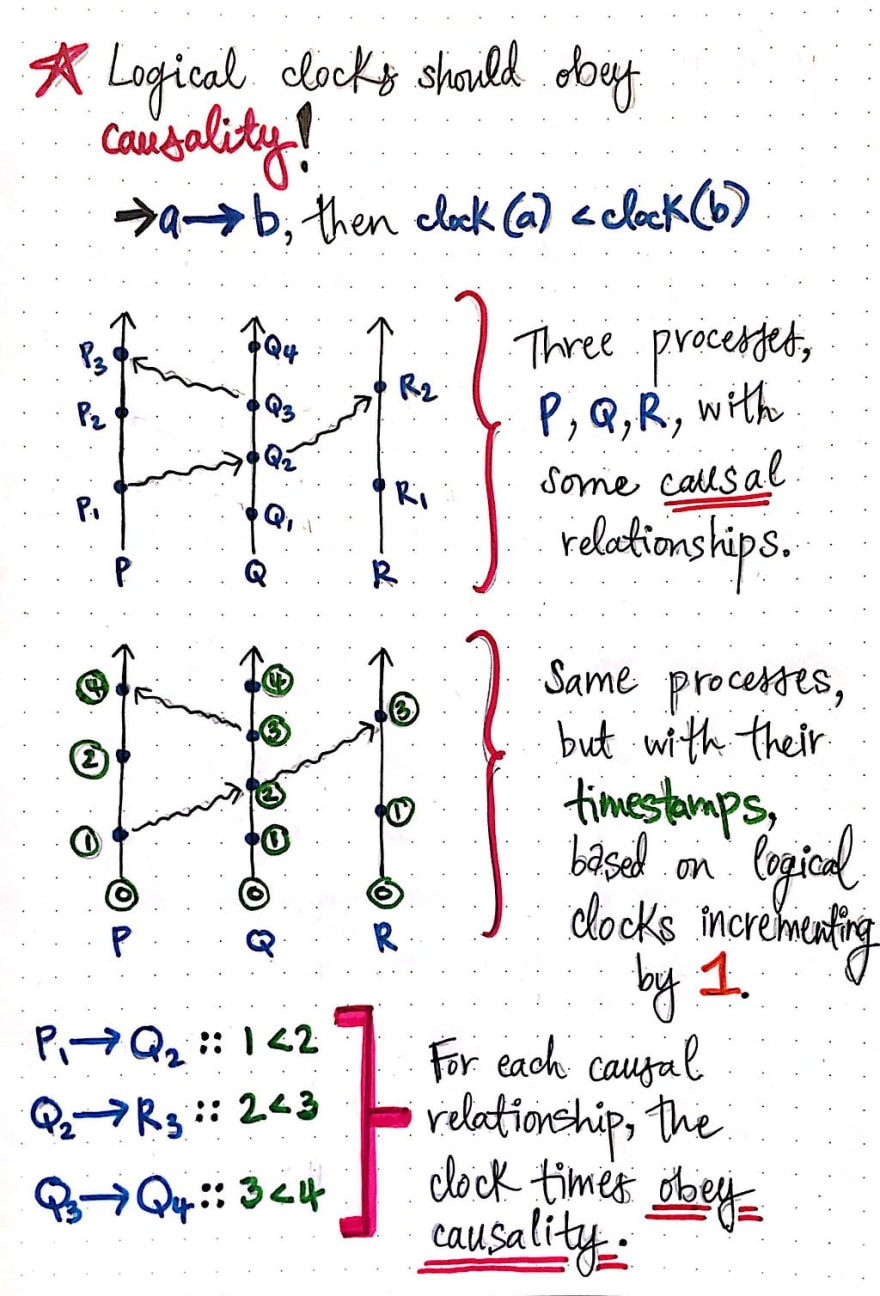
If we take a look at the example shown here, we’ll see that we have a system with three processes, P, Q, and R, with some clear causal relationships between the events in the system.
We can see that event P1 → Q2, because event P1 is the send event of Q2, which is the receive event, and one causes the other. On the other hand, event Q2 → R3, as Q2 sends a message to R3, which is a receive event in and of itself. Similarly, we can see that Q3 → Q4, as they both occur on the same process, one after another.
If we look at these same causal relationships, and compare them with their timestamps, we can see that the clock times for each causal relationship obeys causality as well. For the relationship of P1 → Q2, the clock time for P1 < Q2, as 1 < 2. The same goes for Q2 → R3 (2 < 3) and Q3 → Q4 (3 < 4).
However, the same rule sadly cannot be said of events in the system that are not causally-related! Let’s take a closer look at some of the other events in the same system we saw before. If we examine the events R1 and P2, we’ll see that the time at R1 is 1, while the time at P2 is 2. We might think that, because the clock time of 1 is less than (<) 2, that R1 → P2. But, unfortunately, this is not the case!

In fact, if we look at this system, we’ll se that there is actually no causal path between R1 and P2. These are concurrent events! Concurrent events do not have causal paths from one to another. Thus, because these two events are concurrent, here is no way to be certain that one event happened before the other. We cannot look at their timestamps and guarantee that they are causally-related!

In more abstract terms, we can think of it like this: if event a happens before b, then we can be sure that the timestamp of a will be less than the timestamp of b. But just because a’s timestamp is less than b, we don’t know for sure that a happened before b, because the two events could also be happening at the same time!
For two concurrent events, we cannot make a judgement call about the happens before relationship just based on the clock times of the events. The only thing that we can really guarantee in such a case would be that b does not happen before a.
This is one of the limitations of logical clocks. Indeed, Lamport even acknowledges this in his own paper, and suggests using “any arbitrary total ordering of the processes” in a system to decide how to break ties when two timestamps could very well be equivalent.

Lamport clocks are pretty amazing in their simplicity, but they are admittedly not foolproof. When given a set of partially-ordered events, we can create a total ordering out of them using simple clock counters and can be sure that those clocks and the timestamps they provide us with will always obey causality. However, Lamport clocks do not help us order the concurrent events in a system, or find a causal relationship between them.
There are other kinds of clocks that can be used in a distributed system to help solve this problem, but all of the other solutions came along many years after Lamport first introduced his logical clocks back in 1978. We’re lucky that he did, because he set the stage for a new way of thinking about time in distributed systems, and would end up changing the way we talk about distributed computing forever.
Resources
There are some great resources on Lamport’s paper on logical clocks, as well as causal ordering. If you’re curious to learn more (or read Lamport’s paper yourself), check out the resources below!
- Time, Clocks, and the Ordering of Events in a Distributed System, Leslie Lamport
- Time, Clocks and Ordering of Events in a Dist. System, Dan Rubenstein
- Time and Ordering: Lamport Timestamps, Indranil Gupta
- Lamport’s Logical Clocks, Michael Whittaker
- Logical Clocks, Professor Paul Krzyzanowski



Top comments (1)
Aaaa, Things are getting harder and harder. Anyone here yet? 😅