Hey Guys! Nayan here and this is the 28th day of the 100-DAY challenge. If you are reading this for the first time , I learn and solve some questions throughout the day and post them here.
Today's question is rather a bit popular one. We are going to solve the 3. Longest substring without repeating characters problem.
Problem: Longest substring without repeating characters
Given a string s, find the length of the longest substring without repeating characters.
Example:
Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.
Input: s = "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.
Input: s = "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.
Intuition:
Now that we have got a gist of what the question demands from us, let's take a look at our options, observe and possibly optimize it as well.
I would be lying if I said I don't want to do every problem the Naïve way because that's the exact logical thinking one thinks of regardless.
So let's start with that and then we will see what we can do about it.
Approach: Naïve
- It should look something like this.
- We generate every possible substring of the given string to us. - We can either do this using two pointers i and j and then using another pointer to calculate it's length.
- This is a straight up cubic time complexity approach. I don't like the sound of that, but the approach is simple enough to be understood.
- Can we optimize it is the question. How about every time we are iterating through to generate a substring we check if we have encountered a repeating character.
- We can use a set or map to do this.
- That would increase the space complexity from previously O(1) to O(N) but that would also help reduce time complexity.
- I would say it's a decent trade off looking at our space complexity.
Intuition: Optimal Solution
- We are going to use an approach called sliding window here. This approach reduces our solution down to O(N) time and space complexity.
- It kinda does wonders for strings in many problems , so I suggest reading an article or two about it. Right Now, I am covering questions so I would stick to specific approaches for that question but maybe in the future I will explain algos in depth. As I am still a learner after all.
- Back to the question:
- We are going to use two pointers i and j and initialize them at 0th index.
- We are going to also make a map of characters to check if a character is repeating.
Approach:
- We are going to shift the index right by one.
- If we approach a character that has been found previously, we check if that character's previous index(the one where it was found previously is greater than the left index).
- If it is we are going to shift our left ahead to that previous Index+1 otherwise we will just increment our left by 1.
- We traverse until we reach end of the string and also update our current and global optimum side by side.
- What is the length of a substring at any given moment is right - left + 1.
Dry Run:
I think a dry run is very much needed here in this case so that we can understand the approach.
Code:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int left = 0,right = 0;
vector<int> seen(256,-1);
int n = s.size();
int ans = 0;
while(right < n)
{
if(seen[s[right]] != -1)
left = max(seen[s[right]]+1, left);
seen[s[right]] = right;
ans = max(ans,right-left+1);
right++;
}
return ans;
}
};
Comeplexity Analysis
Time: O(N)
Space: O(N)
Thanks for reading. Feedback is highly appreciated.


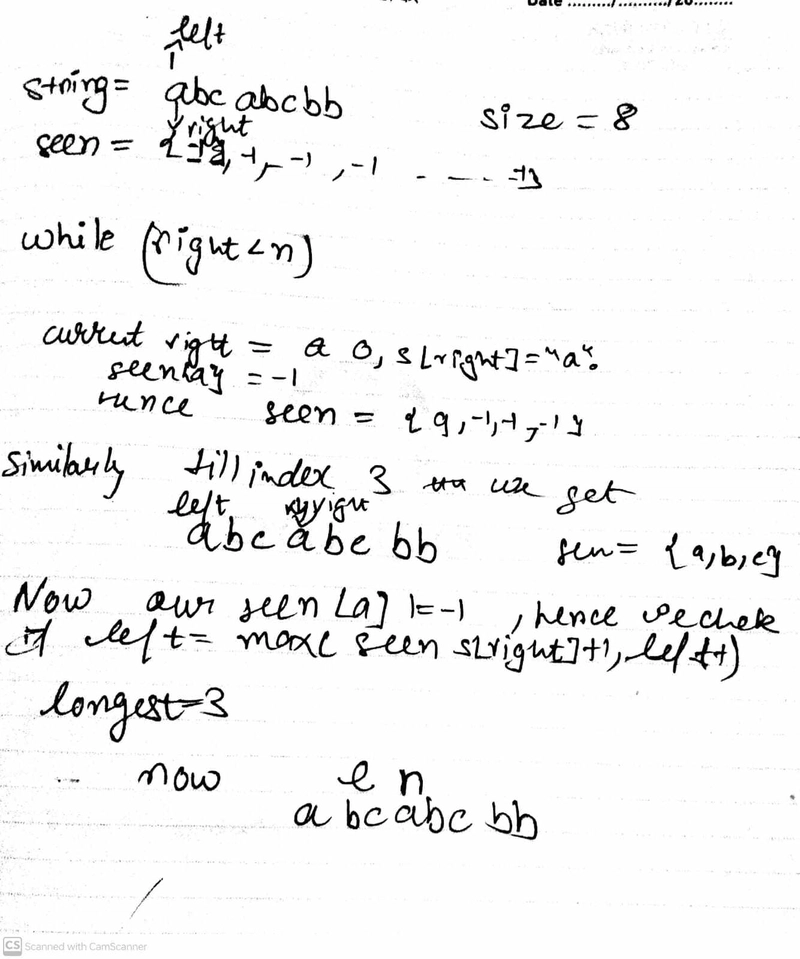

Top comments (0)