DAY 3 - Pascal's Triangle

Hello to anyone reading this. I am still relatively new to coding and this platform as well, so please feel free to drop any corrections/advice for me.
I am trying to do the 100 Day-Challenge of consistent coding and this is Day-3.The goal is simple. I will solve one or more than one leetcode/gfg problem a day and post what I learnt. I am confident that this will help me improve my concepts and help me be more consistent in my practice. Looking forward to a positive interaction with all of you.

DAY-3 PROBLEM 1
Given an integer numRows, return the first numRows of Pascal's triangle.

In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:

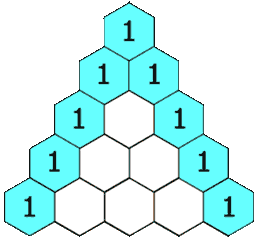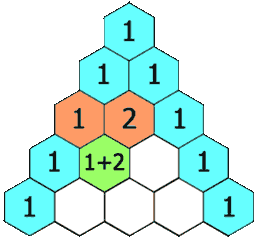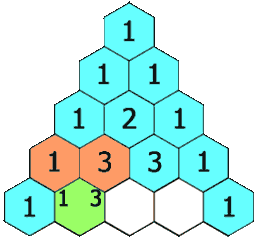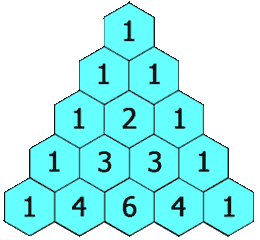
Example:
Input: numRows = 5
Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

This problem is available in three types of variations.

Variation 1: Given row number r and column number c. Print the element at position (r, c) in Pascal’s triangle.

Variation 2: Given the row number n. Print the n-th row of Pascal’s triangle.

Variation 3: Given the number of rows n. Print the first n rows of Pascal’s triangle.

Variation 1:

If we look up the pascal triangle for a row manually we can see that for Variation 1.
If we use the naive approach for solving this, we can either calculate the entire pascal triangle up until that row and then find that element or if we were to calculate it using combinational logic, we will calculate n!, (n-r)! and r!.
Either way this would be a truly time expensive way to solve this problem.
Let's look at the smart way.
If we look closely we can dumb the combinational logic down to
n/1 * n-1/2 * n-2/3 *....(n-r+1)/r.
So we can form up a function to calculate nCr:

int nCr(int n, int r)
{
   long long ans;
for(int i = 0; i < r; i++)
{
   ans = ans*(row-i);
   ans = ans/(i+1);
}
   return ans;
}

This way we can calculate nCr in O(n) time.
If we really look closely at the pascal triangle, we can see that any element at any position of rows and columns is just
(r-1)C(c-1).

So this makes us calculate our answer in O(n) time.
Code:

int nCr(int n, int r)
{
   long long ans;
for(int i = 0; i < r; i++)
{
   ans = ans*(row-i);
   ans = ans/(i+1);
}
   return ans;
}

int pascalElement(int r, int c)
{
   return nCr(r-1,c-1);
}

Time Complexity: O(c), where c = given column number.
Reason: We are running a loop for r times, where r is c-1.

Space Complexity: O(1) as we are not using any extra space.

Variation 2:

Now that we have figured out how to calculate nCr optimally, we might think of calculating nCr for each element of that row and store them in an array.
But that would be a naïve approach. With a small tweak, we can actually find it in less time.

Let's try solving an example:
Input: rowIndex = 3
Output: [1,3,3,1]

• We know that the ending and starting of our resultant row of any pascal triangle's row will always be 1.
• We start from the position 2. We can see that its 3. Let's see it in a combinatorically.
• It's 4-1C2-1 : 3*1/1.
• Next Element is 3/1 * 2/2;
• Next element is 3/1 * 2/2 * 1/3;
• The row is decreasing by one while the column is getting subtracted.

Hence we use this logic and using logic we derived before to calculate the row.
Code:

vector<int> getRow(int rowIndex) {
        long long ans = 1;
        vector<int> ansRow;
        ansRow.push_back(1);
        for(int col = 0; col < rowIndex; col++)
        {
            ans = ans * (rowIndex - col)/(col+1);
            ansRow.push_back(ans);

        }
        return ansRow;        
    }

Complexity Analysis: **
**Time: O(n), Space: O(1)

Variation 3:

Now that we have solved variation 2, variation 3 looks like cheesecake.
Applying the same concept of variation 2 for nth row calculation. We just calculate all rows and store them in a list.

*Code: *

vector<int> generateRow(int row)
    {
        long long ans = 1;
        vector<int> ansRow;
        ansRow.push_back(1);
        for(int i = 1; i < row; i++)
        {
            ans = ans *(row-i);
            ans = ans/i;
            ansRow.push_back(ans);
        }
        return ansRow;
    }
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> ans; numRows;
        for(int i = 1; i <=numRows; i++)
        {
            ans.push_back(generateRow(i));
        }
        return ans;
    }

Complexity Analysis: **
**Time: O(n^2), Space: O(1)

This is how we can calculate pascal's triangle in a very fast way.
As always, Please feel free to advice me or correct me in the comment section. Just here for fruitful learning and consistent practice.