Today's algorithm is a common one:
Count the number of prime numbers less than a non-negative number, n.
If n = 10, the output should be 4, because there are 4 prime numbers less than 10 (2, 3, 5, 7).
As with many of the common algorithms, there are plenty of ways to approach this problem. I recently learned about the Sieve of Eratosthenes, so today I'm going to be implementing it to solve this problem.
What is the Sieve of Eratosthenes?
The Sieve of Eratosthenes is an algorithm used to find all prime numbers less than a number. The way it works is that, starting from 2, it creates a list of all integers from there until n. Then, starting with 2 (which is the smallest prime), every multiple of 2 is marked as not a prime. Next, find the next number that's greater than 2 that hasn't yet been marked as not prime, and repeat the steps--marking its multiples as not prime. The numbers that haven't been marked as "not prime" are, in the end, the list of primes less than the given number.
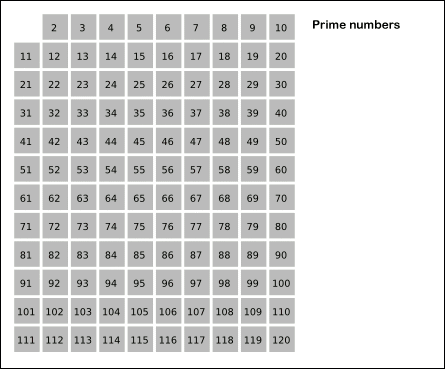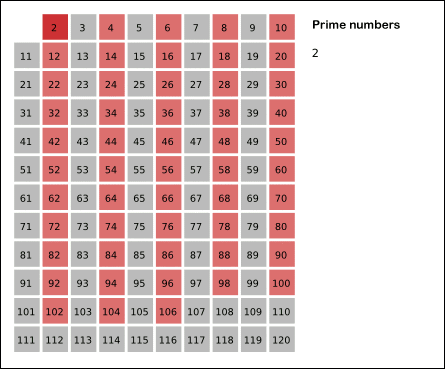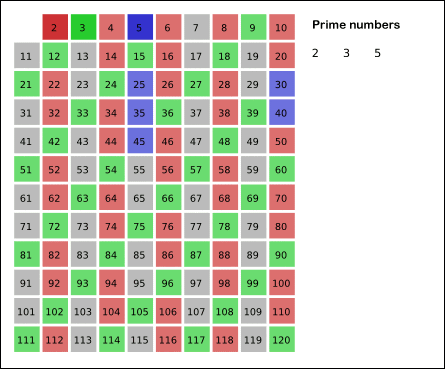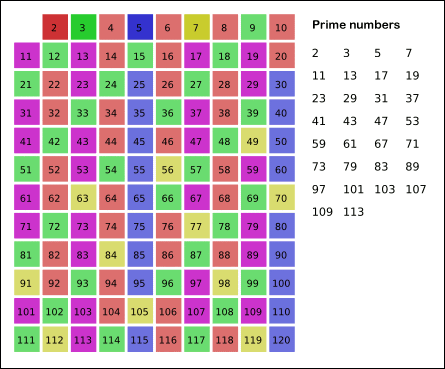
Here's a really neat visual that shows how the algorithm runs when n is 121.
Implementing the Algorithm In JavaScript
The first thing I'll want to do is create an array which will hold booleans representing if each number is prime or not prime. We'll also want to initiate a count, starting with 0, for the number of primes less than the number. We know that that count is what we'll be returning at the end, so we can include that line now.
function countPrimes(n) {
let booleans = []
let count = 0
//...
return count
}
Next, going from 0 until the number, we'll push 'true' to the 'booleans' array. This means that we'll start by assuming that every number is prime.
function countPrimes(n) {
let booleans = []
let count = 0
for (let i = 0; i < n; i++) {
booleans.push(true)
}
//...
return count
}
Now is when we're going to be checking multiples of each prime number, marking them as not prime. We can start this by constructing a for loop that begins at 2 (the smallest prime) and ending at the square root of n. Setting the upper limit to the square root of n cuts down on how many numbers are being checked.
function countPrimes(n) {
let booleans = []
let count = 0
for (let i = 0; i < n; i++) {
booleans.push(true)
}
for (let i = 2; i <= Math.sqrt(n); i++) {
//...
}
//...
return count
}
Now, for each i, we want to see if it's already been marked as not a prime in the booleans array. If it hasn't, then we'll want to have another for loop based on that number.
That inner for loop will start at j = i*i, and go up by i until it reaches n. At every stop, it'll mark that point in the booleans array as false, meaning it's not a prime number. We know all of these numbers are not prime because they're divisible by j.
function countPrimes(n) {
let booleans = []
let count = 0
for (let i = 0; i < n; i++) {
booleans.push(true)
}
for (let i = 2; i <= Math.sqrt(n); i++) {
if (booleans[i]) {
for (let j = i * i; j < n; j += i) {
booleans[j] = false
}
}
}
//...
return count
}
At this point, we have the booleans array, which is filled with a boolean representing if each number is a prime. If n = 5, then booleans would be [true, true, true, true, false], meaning that 0, 1, 2, and 3 are all prime, and 4 is not (*note that 0 and 1, for this exercise, are not actually considered prime, but we'll correct for that).
Now, all that's left to do is count how many times 'true' appears in the booleans array. Because the smallest prime number is 2, we can start the for loop at 2, going up until n. If it's true, we'll increment the count.
function countPrimes(n) {
let booleans = []
let count = 0
for (let i = 0; i < n; i++) {
booleans.push(true)
}
for (let i = 2; i <= Math.sqrt(n); i++) {
if (booleans[i]) {
for (let j = i * i; j < n; j += i) {
booleans[j] = false
}
}
}
for (let i = 2; i < n; i++) {
if (booleans[i]) {
count++
}
}
return count
}
If n = 5, then booleans would be [true, true, true, true, false]. Starting at i = 2, we'd come across true twice, so count = 2.
I'm always on the lookout for cool algorithms, so let me know in the comments if you have a favorite!


Top comments (0)