Today's algorithm is the Add Digits Problem:
Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.
For example, if you were given the number 38, you'd add its digits 3 + 8, getting 11. Because 11 is not a single-digit number, we'd add the digits again, so we'd do 1 + 1, getting 2, which is our result.
In math, this is called the 'Digital Root', and there is a specific algorithm you can use to solve the problem. However, since memorizing algorithms is not a great way to understand problems and build on concepts, I'll instead approach this problem using while loops and modulo.
Approaching the Add Digits Problem
I want to approach this problem by using modulo. Modulo (%) is an operator which returns the remainder after dividing one number by another. For example, 10 % 3 would give us the result of 1, because 10/3 is 3, remainder 1. I like using modulo in these kinds of problems because combining modulo 10 (%10) with division enables us to separate the digits in a number.
To illustrate what I mean, we can use an example. Let's say we're given the number 15, and we wanted to separate the 1 and 5.
let number = 15
number % 10 // this gives us 5
Math.floor(num / 10) // this gives us 1
In this problem, we want to separate the digits and add them, and keep doing that as long as the sum is more than 1 digit. There are two main processes that are repeated in this approach: summing the digits, and separating the digits. We want to repeat both of these processes a number of times, and therefore we'll want to have nested while loops. The outer while loop will keep executing as long as the result we're working with is greater than or equal to 10 (a.k.a., it's not a single digit). The inner while loop will keep executing as long as the numbers still can be separated, which means as long as the number we're working with is greater than 0.
Coding the Solution to the Add Digits Problem
We'll start by setting up the nested for loops that we discussed in the approach above.
function addDigits(num) {
while (num >= 10) {
//...
while (num > 0) {
//...
}
}
//...
}
Inside the first while loop, we'll initialize a variable called sum, setting it equal to 0. Each time we start this while loop, we'll want to reset the sum equal to 0.
function addDigits(num) {
while (num >= 10) {
let sum = 0;
while (num > 0) {
//...
}
//...
}
//...
}
Now, inside the inner while loop is where we split num into its separate digits using modulo and division. We'll add the last digit of num to sum using num % 10, and then we'll modify num using division to effectively remove the last digit.
function addDigits(num) {
while (num >= 10) {
let sum = 0;
while (num > 0) {
sum += num % 10;
num = Math.floor(num / 10);
}
//...
}
//...
}
When the inner while loop is done executing for the first time, we have the sum of the digits the first time we split them. However, it's very possible that this sum will be a number greater than or equal to 10, in which case we'll need to go through the loop again. Therefore, we'll set num equal to sum, and the loop may execute again.
Finally, outside of of the larger while loop, we'll return num.
function addDigits(num) {
while (num >= 10) {
let sum = 0;
while (num > 0) {
sum += num % 10;
num = Math.floor(num / 10);
}
num = sum;
}
return num;
}
Going Through an Example
Let's say we're given the number 38. First, we'll ask: is num greater than or equal to 10? It is, so we'll enter the larger while loop, where we will immediately set sum equal to 0.
Now we're met with the second while loop. Is 38 greater than 0? It is, so we'll enter the while loop. We'll do 38%10, which gives us 8, and add it to sum, so sum equals 8. We'll also set num equal to Math.floor(38/10), which is 3.
Now we've executed the inner while loop for the first time. Num is 3, which is greater than 0, so we'll execute the inner while loop again. We'll do 3%10, which gives us 3, and add that to sum, making sum equal 11. We'll also set num equal to Math.floor(3/10), which is 0.
We've executed the inner while loop a second time. This time, num = 0, so we won't execute it again. We can now set num equal to sum, so num = 11.
Now we can look at the outer while loop again. Is num greater than or equal to 10? Yes, so we'll enter the outer while loop again. We'll set sum equal to 0 again.
Is num, which is 11, greater than 0? Yes, so we'll enter the inner while loop again. We'll do num%10, which is 1, and add that to sum, making sum = 1. We'll also modify num, and set it equal to Math.floor(11/10), which is 1.
We've executed the inner while loop once, so now we can check: is num, which is 1, greater than 0? Yes, so we'll enter the inner while loop again. Again, we'll do num%10, which is 1%10, which is 1, and add it to sum, giving us sum = 2. We'll then set num equal to Math.floor(1/10), which is 0.
We've executed the inner while loop, but this time num = 0, so we won't execute it again. So, we can set num = sum, which means num = 2.
We'll check if we should go through the outer while loop again by asking, is num >=10? Since num is 2, that's not true, so we won't enter the while loop again. Therefore, we'll just return num, which is 2.
--
Let me know if you have any questions or alternative solutions!





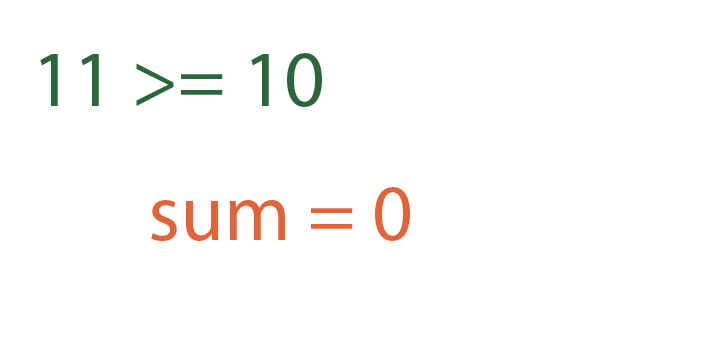




Top comments (7)
I would write this in js
const digitalRoot = (num)=>{return num < 10 ? num:digitalRoot([...(num+"")].reduce((a,b)=>(+a)+(+b)))
}
Super elegant!
Alisa, I have a suggestion... It would be great if you can add all your DSA solution explanation posts into one series, it will be easier to juggle between posts! :)
Thanks for your regular posts, they are of great help.
The fun part about the digit sum is that it behaves like a modulo with 9, so this here works:
const digitSum = n => n<10 ? n : (n-1) % 9 + 1;
Hey man! This is new, I see this works! Could you please explain (or refer to) the math behind this or how this works as a modulo 9? Thanks!
I can’t really explain it in a few words but I hope this helps: flyingcoloursmaths.co.uk/a-neat-nu... :)
Brilliant Solution , Math Saves the day !