Padding in Neural Network

this post is originally from https://www.machinecurve.com/index.php/2020/02/07/what-is-padding-in-a-neural-network/

What is padding and why do we need it?

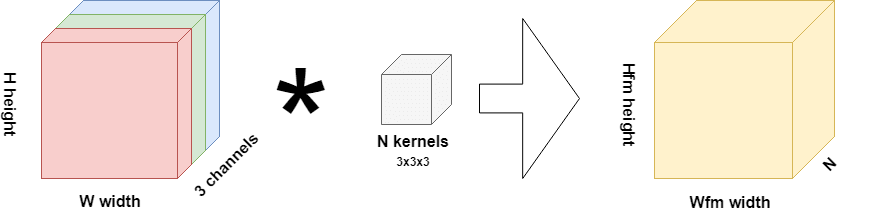
What you see on the left is an RGB input image-width $W$ , height $H$ and three channels. Hence, this layer is likely the first layer in your model, in any other scenario, you'd have feature maps as the input to your layer.

Now, what is a feature map? That's the yellow block in the image. It's a collection of $N$ one-dimensional maps that each represent a particular feature that the model has spotted within the image. This is why convolutional layers are known as feature extractors.

Now, this is very nice-but how do we get from input (whether image or feature map) to a feature map? This is through kernels or filters, actually. These filters-you configure some number $N$ per convolutional layer-"slide"(strictly, convolve) over your input data, and have the same number of "channel" dimensions as your input data, but have much smaller widths and heights. For example, for the scenario above, a filter maybe 3x3 pixels wide and high, but always has 3 channels as our input has 3 channels, too.

Now, when they slide over the input-from left to right horizontally, then moving down vertically after a row has been captured-they perform element-wise multiplications between what's currently under investigation within the input data and the weights present within the filter. These weights are equal to the weights fo a "classic" neural network, but are structured in a different way. Hence, optimizing a ConvNet involves computing a loss value for the model and subsequently using an optimizer to change the weights.

Through these weights, as you may guess, the model learns to detect the presence of particular features-which once again, are represented by the feature maps.

Conv layers might induce spatial hierarchy

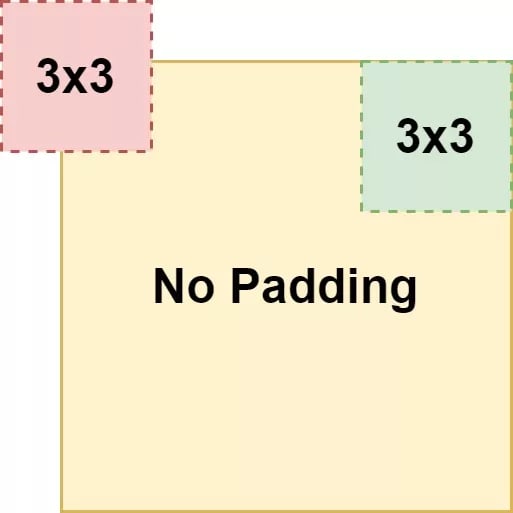
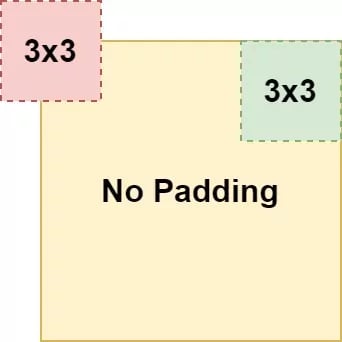
If the width and/or height of your kernels is above 1, you'll see that the width and height of the feature map (being the output) getting smaller. This occurs due to the fact that the feature maps slides over the input and computes element-wise multiplications, but is too large in order to inspect the "edges" of the input. This is illustrated in the image, where "red" position is impossible to take and the "green" ones is part of the path of the convolution operation.

As it cannot capture the edges, it won't be able to effectively "end" at the final position of your row, resulting in a smaller output width and/or height.

We call this a spatial hierarchy. Indeed, convolutional layers may cause a "hierarchy"-like flow of data through the model. Here, you have a schematic representation of a substantial hierarchy and a less substantial one-which is often considered to be less efficient.

Padding avoids the loss of spatial dimensions

Sometimes, however, you need to apply filters of a fixed size, but you don't want to lose width and/or height dimensions in your feature maps. For example, this is the case when you're training an autoencoder. You need the outptut images to be of the same size as the input, yet need an activation function like Sigmoid in order to generate them.

If you do so with a Conv layer, this would be problematic, as you'd reduce the size of your feature maps-and hence would produce outputs unequal in size as your inputs.

That's not what we want when we create an autoencder. We want the original output and the original output only.

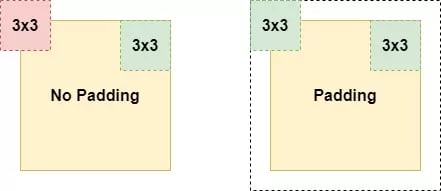
Padding helps you solve this problem. Applying it effectively adds space around your input data or your feature map-or more precisely, "extra rows and columns".

The consequence of this fact are rather pleasurable, as we can see in the example above. Adding "extra space" now allows us to capture the position we previously couldn't capture, and allows us to detect features in the edges of your input.

Types of padding

Now, unfortunately, padding is not a binary option-i.e. it cannot simply be turned on and off. Rather, you can choose which padding you use.

Valid padding/no padding

Valid padding simply means "no padding". This equals the scenario where capturing edges only is not possible.

It may seem strange to you that frameworks include an option for valid padding/no padding, as you could simply omit the padding as well. However, this is not strange at all: if you specify some padding attribute, there must be a default value.

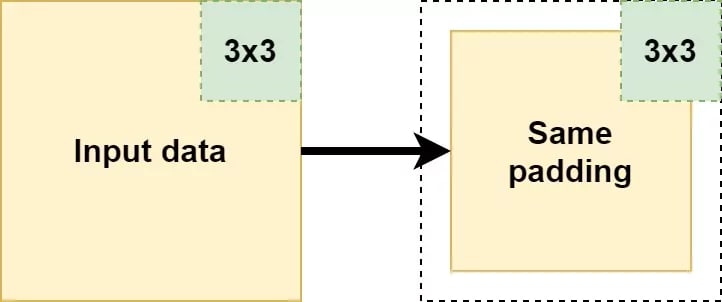
Same padding/zero padding

Another option would be "same padding" also known as "zero padding". Here, the padding ensures that the output has the same shape as the input data. It is achieved by adding "zeros" at the edge of your layer output, e.g. the white space on the right of the image.

Casual Padding

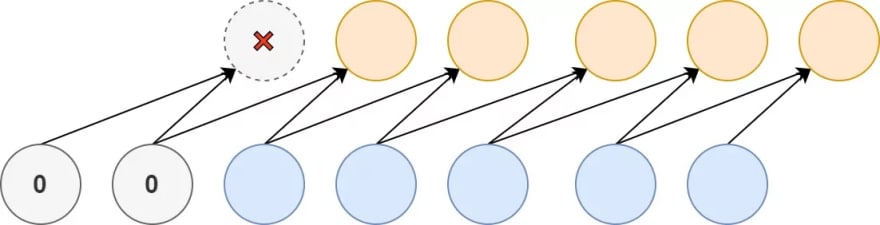
Suppose that you have a time series dataset, where two inputs together determine an output, in a causal fashion. It's possible to create a model that can handle this by means of a Conv1D layer with a kernel size of 2-the learnt kernel will be able to map the inputs to the outputs successfully.

But what about the first two targets? Although they are valid targets, the input are incomplete-that is, there is insufficient input data available in order to successfully use them in the training process. For the second target, one input-visible in gray-is missing (whereas the second is actually there), while for the first target both aren't there.

For the first target, there is no real hope for success (as we don't have any input at all and hence do not know which values produce the target values), but for the second, we have a partial picture: we've got half the inputs that produce the target.

Causal padding on the Conv1D layer allows you to include the partial information in your training process. By padding your input dataset with zeros at the front, a causal mapping to the first, missed-out targets can be made. While the first target will be useless for training, the second can now be used based on the partial information that we have.

Reflection padding

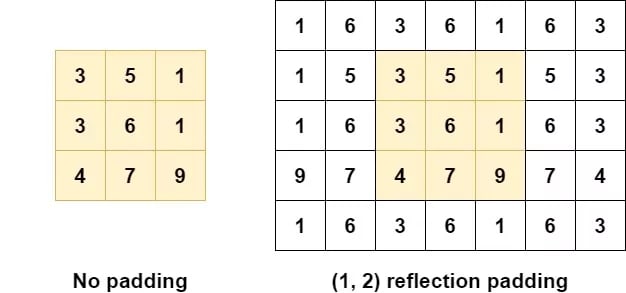
Another type of padding is "reflection padding". As you can see, it pads the values with the "reflection" or "mirror" of the values directly in the opposite direction of the edge of your to be padded shape.

For example, if you look at the image above, for the first row of the yellow box: if you go to the right, you'll see a 1. Now you need to fill the padding element directly to the right. What do you find when you move in the opposite direction of the edge? Indeed, a 5. Hence, your first padding value is a 5. When you move further, it's a 3, so the next padding value following the 5 is 3. And so one. In the opposite direction, you get a mirrored effect. Having a 3 at the edge, you'll once again find 5 (as it's the center value) but the second value for the padding will be a 1. and so on.

Reflective padding seems to improve the empirical performance of your model. Possibly, this occurs because of how "zero" based padding (i.e. the "same" padding) and "constant" based padding alter the distribution of your dataset. This becomes clear when we actually visualize the padding when it is applied:

Replication Padding/Symmetric Padding

Replication padding looks like reflection padding, but is slightly different. Rather than reflecting like a mirror, you simply take a copy and mirror it. Like this: You're at the first row again, at the right. You find a 1. What is the next value? Simple: you copy the entire row, mirror it, and start adding it as padding values horizontally. As you can see, since we only pad 2 elements in width, there are 1 and 5, but 3 falls off the padding.

As with reflection padding, replication padding attempts to reduce the impact of "zero" and "constant" padding on the quality of your data by using "plausible" data values re-using what is along the borders of the input.

Which padding to use when?

There are no hard criteria that prescribe when to use which type of padding. Rather, it's important to understand that padding is pretty much important all the time-because it allows you to preserve information that is present at the borders of your input data, and present there only.