In this series of posts, I will discuss coding questions on the LinkedList Data structure.
The posts in this series will be organized in the following way,
- Question Link ❓
- Possible Explanation 📝
- Documented C++ Code 🧹
- Time and Space Complexity Analysis ⌛🌌
The Question
Given the head of a linked list, remove the nth node from the end of the list and return its head.
Constraints:
- The number of nodes in the list is
sz. 1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
https://leetcode.com/problems/remove-nth-node-from-end-of-list/description/
💡 Give yourself atleast 15-20 mins to figure out the solution :)
There are two approaches possible, in this post we will see the first one.
Approach 1: Two Pass
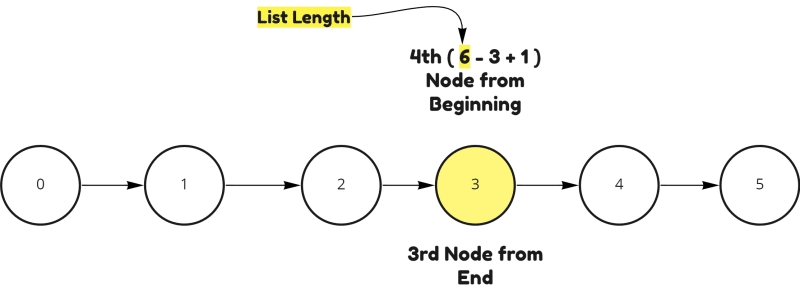
If you think a bit, nth node from end is list_len - n + 1 th node from beginning.
So our algorithm is:
- Find the length of LinkedList → L
- Delete the (L - n + 1)th node from beginning.
C++ Code
Definition of LinkedList
//Definition for singly-linked list.
struct ListNode
{
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
Solution
ListNode *removeNthFromEnd(ListNode *head, int n)
{
//- if LL is empty
if (!head)
return head;
//note: first pass : O(n)
//- getting length of LL
int cnt = 0;
ListNode *temp = head;
while (temp)
{
cnt++;
temp = temp->next;
}
//* Standard Procedure to delete (k+1)th node from beginning
//note: Required Node: (cnt - n +1)th node
//note: we have to go "cnt-n" times deep to stand at required node
int k = cnt - n;
ListNode *cur = head;
ListNode *prev = nullptr; //it will point one node preceding to cur
//note: second pass :O(n)
while (k > 0)
{
prev = cur;
cur = cur->next;
k--;
}
//- first node of the LL is to be deleted
if (!prev)
{
temp = cur;
cur = cur->next;
delete temp;
head = cur; //! cur is the new head
}
else
{
prev->next = cur->next;
delete cur;
}
return head;
}
Complexity Analysis
N is the length of LinkedList.
K is the postion of node from end.
Time Complexity: O(N)
Space Complexity: O(1)
We didn't use any extra space.
💡 It turns out there's a better method to solve this question in single pass, we shall see that method in next post :)

![Cover image for LinkedList Questions: [Two Pass] Delete nth node from end](https://media2.dev.to/dynamic/image/width=1000,height=420,fit=cover,gravity=auto,format=auto/https%3A%2F%2Fdev-to-uploads.s3.amazonaws.com%2Fuploads%2Farticles%2Fq5l1f3elkzckvzja18qa.png)


Top comments (0)