If you saw my article about Selection Sort it means that you already know at least one sorting algorithm. Now that you have a sorted list (or can create one) we are gonna dive in an algorithm that can search for an element in this sorted list, that's gonna be the Binary Search algorithm. We are gonna talk about two approach's to this algorithm, iterative and recursive and about it's time complexity too.
Like I did in all my A&DS Implementation articles with java until now we are gonna create two files.
Iterative Search
Let's start creating the BinarySearch.java file.
This file is gonna hold both our Iterative and recursive search methods. But first we will make the iterative one, iterativeSearch
void iterativeSearch(int[] arr, int key) {
//just a placeholder
int index = 0;
//defines the first one in the array
int first = 0;
//defines last one in the array
int last = arr.length - 1;
//defines the mid point of this array
int mid = (first + last)/2;
}
The first thing we do is create two parameters for our method, the array and the key (or value) we want to search inside this array, the we create the variables we are gonna be using, the index is gonna be the variable that stores the position of the value we are searching (the index of the key). The first variable is the index for the first value in the array (which is 0 because every array starts at 0). The last is the index of the last value in the array which we can get by subtracting one from the size of our array. And finally the mid variable that stores the mid point of our array.
IMPORTANT: Why we get the mid point of the array by using the sum of the first with the last divided by two instead of just getting the last/2 ? We need to make a sum with the first because when we start iterating, the first position of the array is gonna start to change, incrementing every time the loop is completed, making the mid point of the array change too.
Now that we have our variables all set we are going to create the logic to search for the key
//while the array is not the size of zero
while(first <= last) {
if (arr[mid] < key) {
//shifts to the right since is greater and we already checked mid
first = mid + 1;
}
//if item in mid make it equal index, break the loop and return at the end
else if (arr[mid] == key) {
//define index as mid
index = mid;
//print result
System.out.println("The position of " + key + " is " + index);
//break from the while loop
break;
}
else {
//shifts the end point to the left of mid
//since the value is smaller and we already checked the mid
last = mid - 1;
}
// make new count now with the new value to first or last
mid = (first + last)/2;
}
Okay, here we have a basic while loop that iterates until the variable first(that stores the start of the array) is bigger than the last which means that we are gonna iterate until the end of the list. Inside the loop we start creating our conditions to find our element. The way binary search is by dividing the list by half until it finds the number (that's why we make the mid variable) and here is where our conditions play. in the first if statement we make so if the number in the mid is smaller than the key (element we are searching) we will update the variable first to be the position after the mid position, which means we are gonna now search only the right half of the list, because everything to the left is smaller than our key so the key is not gonna be there.
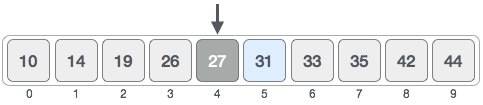
Example images (taken from tutorialPoint)
In this example 31 is the key
After we defined our key we define the mid point of the list (in this case 27)
Then we enter in our loop and met our first condition, comparing if mid value is lower than key
The condition is met so we define first to be the element left to mid (in this case the 31 itself, or position 5) and we repeat the loop
The next condition is if the mid point value is equal to key, if it is the element was found and we can break the loop, here we use the index variable just to get more understandable in print.
Last but not least we make our final condition that is really similar to our first condition, in this case (although not explicitly told in the statement ) checks if the mid value is greater than the key, if it is we are gonna search only the left half of the list, by defining last as the value before the mid point.
The last thing we have in our while loop that is executed in every loop is the mid = (first + last)/2; , This is necessary because every time the loop is executed we make new comparisons with mid and update what we are searching in the list, and if we update the first variable and last variable but don't update our mid variable we will continue with the same mid point every time so the loop is going to make the same comparisons every time.
if (first > last) {
System.out.println("Not found");
}
}
The last thing in out iterativeSearch method is just a simple condition to make sure that, if the loop ends and the key wasn't found, the key is not in the list so we print "not found".
Okay now that we created our method lets create our BinarySearchMain.java to run it!
public class BinarySearchMain {
public static void main(String args[]) {
BinarySearch binary = new BinarySearch();
int[] arr = {10, 6, 4, 8, 2};
int key = 8;
binary.iterativeSearch(arr,key);
}
}
Here we just make a main method and call our iterativeSearch passing the array and key we defined,now everything is working! Just try to run it and play around with different arrays.
In the above case the output should be this
The position of 8 is 3
Time Complexity
The time complexity of iterative search is O(log n) because in the worst case scenario (if the number we are looking for is at the end of the list or is not in the list) we will have to divide the list in half repeatedly until we get to the end of the list. The best case scenario would be O(1) ( or Ω(1) ) and it would be if the element we are looking for is already in the mid point of the array.
Recursive Search
Since we already covered the iterative approach I'm gonna be more to the point in the recursive one
int recursiveSearch(int[] arr, int key, int first, int last) {
//just a placeholder
int index = 0;
int mid = (first + last)/2;
//base case
if (first > last) {
return -1;
}
if(arr[mid] < key) {
//return recursive but with first being shifted right from
//mid getting only the right half of the array
return recursiveSearch(arr,key,mid + 1, last);
}
else if (arr[mid] == key) {
//recursive is gonna end up here at the end
index = mid;
//return the value
return index;
}
else {
//return recursive but with last being shifted left from mid
//getting only the left half of the array
return recursiveSearch(arr,key,first, mid - 1);
}
}
The recursive search is pretty simple, we start by making our recursiveSearch method . The difference is that this time instead of making it a void we make it as an int, so we can use the returns to make our recursion. The other difference in the method is that we add more two parameters: the int first and the int last.
Inside the method we have a base case that comes at the top of the code that if our first is higher than the last our element is not in this list. After that we have our set of conditions similar to what we have done in the iterative search. But inside this if statements we have our return statements. Here is where we are gonna use the power of recursion, we call the same recursiveSearch again in our first if statement and pass the same array,key and last. But we pass our first as mid + 1 making it shift the start of the array to only the right half of the array.
In our next if we do basically the same thing to check if our key is in mid.
Our last check in else is where we use the same concept of our first if but we shift the last to the left half of the array.
And we are done with the recursive search, now we only need to add to main to run it.
int first = 0;
int last = arr.length - 1;
int recursive = binary.recursiveSearch(arr, key, first, last);
if(recursive == -1) {
System.out.println("Not found");
}
else {
System.out.println("Found at position " + recursive);
}
if it returns -1 as we defined in our base case, we print "Not found". else, we found the position so we just print it!
and this is the output (used the same test I used to iterative search)
Found at position 3
Time complexity
Maybe you realized something peculiar about it but... The time complexity of recursive search is the same O(log n) of our iterative search! In the worst case scenario we are still dividing the list by half multiple times. And the best case scenario is still O(1) or ( Ω(1) )
So, you may be asking yourself "What is the difference?" Honestly the only difference is in Space complexity but that is some content for another whole article. So in the end is a matter of choice, which one you find easier to understand? Go and use it!
If you want to see the full code you can see it here in this github repo
This is a post I have started writing in the end of 2020 but I got back to it only in 2021. Because of that I felt like it wasn't good enough and wasn't sure if I should post it or not. I decided to post because if it really bad, the worst thing it can happen is not be useful for someone, if it's not that bad it can still help someone. But just letting stay inside my computer for no reason just doesn't even have a chance to help someone.
If you have any suggestions or critics about what I should write or/and how I should write (more detailed? less detailed?) or even how is my grammar (not a native English speaker) feel free to put it in the comments, It would help me a lot!




Top comments (0)