Continuando os meus estudos do post Séries Temporais: Parte 1, onde abordei alguns conceitos básicos de séries temporais e preparação dos dados. Nesse post falo mais sobre alguns modelos chave para esse tipo de análise.
Autocorrelação e Autocorrelação parcial
Uma análise de série temporal simples é sempre uma análise sobre o que já aconteceu na própria série e com a correlação não seria diferente. Uma correlação nos diz o quão relacionado é um valor com outro valor (isso não significa que um valor influenciou o outro) e uma autocorrelação (ACF) é quando comparamos o valor do presente com valores do passado da mesma série. A diferença entre a autocorrelação e a autocorrelação parcial (PACF) é quase um detalhe: em uma ACF temos a correlação direta e indireta e em uma PACF apenas a correlação direta. Exemplificando, com a ACF vemos a correlação direta do mês de janeiro em março e também a correlação indireta que o mês de janeiro teve em fevereiro que também teve em março.
Conseguimos ver a ACF e PACF de um jeito bem simples com esses dois gráficos da biblioteca statsmodels:
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(df.meantemp)
plot_pacf(df.meantemp)
plt.show()
O intervalo de confiança por padrão é 95%, mostrado como essa marca azul. Observações que estão para fora da marca são consideradas estatisticamente correlacionadas.
White Noise
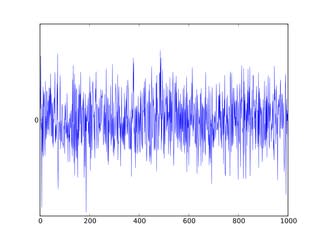
Uma série white noise é uma série na qual a média 0, a variância é constante ao longo da série toda e não há correlação entre os períodos de tempo. O valores de uma série white noise são totalmente aleatórios, ou seja, essa é um tipo de série que não é previsível.
Visão de uma série White Noise
As séries temporais são compostas por uma componente de white noise e a componente dos sinais (outras componentes que explicam os dados). Por esse motivo esse tipo de série é usada na avaliação de modelos. Quando o erro gerado por um modelo é white noise significa que toda a parte previsível dos dados foi ajustada ao modelo e restou apenas o que era aleatório.
Modelos para Séries Temporais
Autorregressão (AR)
Para quem já está habituado ao conceito de regressão esse tipo de modelo é bem simples. Se você não conhece como uma regressão funciona, eu explico nesse outro post aqui.
Uma autoregressão é basicamente uma regressão onde seus parâmetros são regressões em tempos anteriores.
X(t) = a + b1*X(t-1) + b2*X(t-2)
Onde a, b1 e b2 são os coeficientes da regressão e t é o indicador de qual tempo estamos usando na regressão X.
from statsmodels.tsa.ar_model import AR
ar = AR(df)
ar_fit = ar.fit()
predicted = ar_fit.predict(start=len(df), end=len(df)+7)
#ao contrário da maioria dos modelos de machine leaning, quando usamos o predict em séries temporais colocamos o início e fim das predições, como índice ou como datas
ar_fit.k_ar #Essa função mostra o Lag usado na função
Lag operator = número de períodos anteriores
Moving Average Model (MA)
Apesar do nome o Moving Average Model não é a mesma coisa que apenas calcular a média móvel da série temporal. O MA é um modelo linear, assim como a regressão, que usa os resíduos dos passos anteriores como variáveis. Esses resíduos são calculados a partir da diferença com a média dessa série, tendo uma série que se move em volta da sua média.
Onde μ é a média da série, ε são os resíduos de acordo com o tempo t até t-q e θ são os coeficientes de cada variável.
O modelo MA pode ser usado como parte do modelo ARMA (AR + MA) deixando a ordem da AR em zero.
from statsmodels.tsa.arima_model import ARMA
ma = ARMA(df, order=(0, 3))
ma_fit = ma.fit()
predicted = ma_fit.predict(len(df), len(df)+3)
Autoregressive Integrated Moving Average (ARIMA)
Esse modelo é uma combinação dos dois últimos modelos que eu apresentei aqui (Autorregressão e MA), mas não somente isso (porque aí estaríamos falando do modelo ARMA que não vou explicar aqui). Esse modelo também leva em consideração que os dados não apresentam estacionariedade, o que nos leva a parte Integrada (I), que é a utilização dos dados diferenciados uma ou mais vezes, ao invés dos dados “crus”.
Então, basicamente, ao invés de predizer uma série temporal baseada nela mesma em seus períodos anteriores, ARIMA prediz uma série temporal baseada na diferença entre um período e outro anterior.
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(df, order=(4, 1, 0))
#No ARIMA a ordem é para a AR, as diferenciações e a MA, respectivamente.
model_fit = model.fit()
predicted = model_fit.predict(len(df), len(df)+3)
Exponential Smoothing / Suavização exponencial
Esse modelo ainda é um modelo linear, como todos que eu mostrei aqui que, ignorando certa complexidade, são uma soma ponderada dos períodos anteriores da série. A diferença da suavização exponencial é que os coeficientes da soma do modelo linear vão caindo exponencialmente, fazendo com que os períodos mais próximos sejam “mais importantes” na conta do que os períodos mais antigos.
Usando a suavização exponencial simples como exemplo, temos um fator alpha multiplicado pelos coeficientes e variáveis. Esse alpha é um valor entre 0 e 1, sendo que um alpha grande aumenta a diferença da “importância” entre os períodos próximos e os antigos, e um alpha muito pequeno diminui essa diferença.
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
model = SimpleExpSmoothing(df)
model_fit = model.fit()
predicted = model_fit.predict(len(df), len(df)+3)
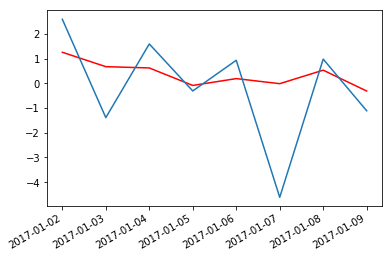
Aqui estão alguns resultados quando apliquei esses modelos ao dataset com o clima da cidade de Delhi, o mesmo que usei na parte 1 desse post. Usei os dados já diferenciados.
Autorregressão:
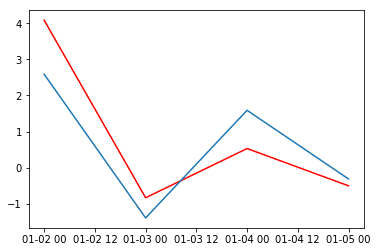
ARIMA
Referências
11 Classical Time Series Forecasting Methods — Machine Learning Mastery
Time Series Talk — YouTube



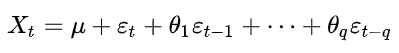

Top comments (0)