Séries temporais são conjuntos de dados onde o tempo guia todas as outras variáveis. Pode conter qualquer forma de tempo, anos, dias, minutos, etc. Essa ideia de ordem temporal no conjunto de dados faz com que as análises das séries sejam um pouco diferentes.
Existe todo um campo de estudo em volta do assunto e, mesmo escrevendo sobre conceitos básicos, terei mais do que um artigo para abordar o tema (que também estou estudando). Nesse artigo vamos ver uma introdução a séries temporais, suas componentes e estacionariedade.
Antes de tudo precisamos preparar os nosso dados para a análise. Muitos datasets apresentam o tempo como uma string então a primeira coisa a se fazer é a conversão para o tipo Date. Também vamos passar essa coluna para o index do dataframe e plotar os dados logo depois. Esse dataset possui informações sobre o clima da cidade Delhi — Temperatura média, humidade, velocidade do vento e pressão.
import pandas as pd
import numpy as np
from matplotlib import pyplot as pltdf = pd.read_csv("DailyDelhiClimateTest.csv")
df.date = pd.to_datetime(df.date)
df = df.set_index('date')
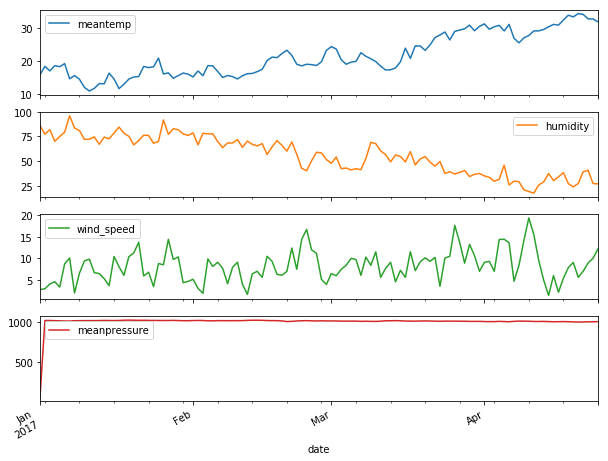
df.plot(subplots=True, figsize=(10,8))
Esses dados são diários e eu vou trabalhar com eles assim, entretanto, podemos trabalhar numa frequência de tempo diferente usando a função resample . Como exemplo vou redimensionar os dados para mostrar por meses, agrupando os valores pela média e também vou redimensionar por hora e preencher os campos nulos que aparecem por não termos informações tão granuladas.
#Por mês:
df_exemple.resample('M').mean()
#Por hora:
#Ffil preenche com o último valor anterior aos campos
df_exemple.resample('H').ffill()
#Bfil preenche com os campos com o próximo valor válido na caluna
df_exemple.resample('H').bfill()
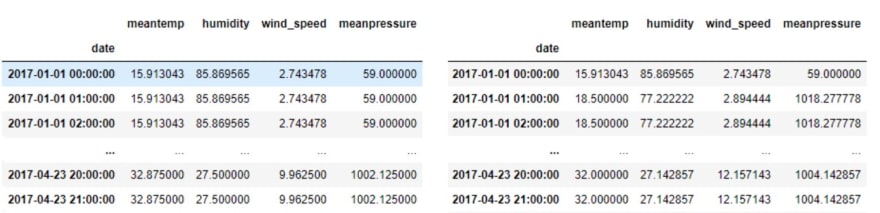
método ffill versus método bfill
Agora, para fazer as análises é preciso entender as séries temporais. Do modo como esse dataset está montado podemos tratar cada coluna como uma série. E as séries temporais são compostas por 4 componentes:
Tendência / Trend
Aqui é a tendência dos dados de crescer ou diminuir em longo período de tempo. Essa análise pode ser feita observando um gráfico de linha, onde conseguimos ver um crescimento ou uma diminuição suave com o tempo.
Sazonalidade
Essa é uma variação dos dados que se repete, de acordo com algum padrão, dentro de um curto intervalo de tempo bem definido (um ano no máximo). Podemos observar a sazonalidade no trânsito, que aumenta sempre nos horários de começo e fim de expediente, ou nas vendas de sorvete que aumentam sempre no verão e caem sempre no inverno.
Ciclicidade
Também é uma variação nos dados observada com algum padrão só que em longos períodos de tempo (mais de um ano) que nem sempre são iguais. Como a venda de casas, que por mais que possa ter alguma sazonalidade durante o ano, tem um ciclo de altas e baixas vendas quando observadas ao longo de décadas.
Resíduos / Ruído
São variações que não são explicadas pelas variáveis do dataset. Em geral são aleatórias.
A biblioteca “Statsmodels” é uma grande amiga quando o assunto é séries temporais. Vou usá-la para mostrar a decomposição da série da coluna meantemp (temperatura média). O resultado da função seasonal_decompose é um conjunto de séries dessa decomposição que você pode plotar como quiser.
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(df.meantemp)
result.plot()
plt.show()
Existem dois modos nos quais as componentes podem se relacionar com os seus dados, o modelo aditivo onde suas observações são fruto dessas componentes somadas e o modelo multiplicativo onde as componentes são multiplicadas. A componente cíclica é mostrada junto da componente de resíduos pois as duas não possuem um tempo certo de acontecimento.
Estacionariedade
Para trabalhar com séries temporais precisamos que ela seja estacionária. Essa característica além de ser necessária para algum modelos, facilita a projeção dos dados.
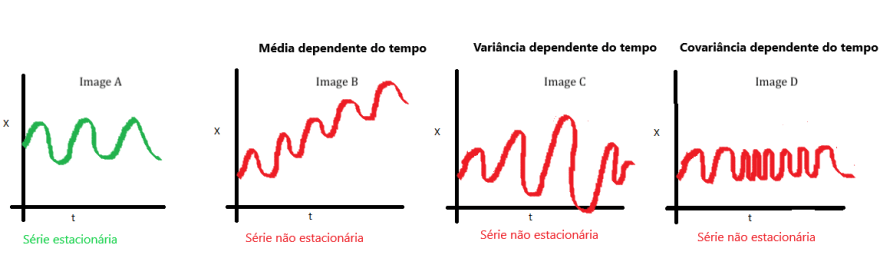
Simplificando bastante podemos entender a estacionariedade como uma série temporal com sua média, variância e co-variância permanecendo iguais quando comparados os períodos de tempo da série, ou seja, as estatísticas da série não sofrem variações com o tempo, não são dependentes dele.
A “forma” dos dados nos gráficos podem nos dar uma noção se a série é ou não estacionária. Uma maneira legal de enxergar isso é plotando as estatísticas de rolagem, isso é, ao invés de mostrar todas as observações ou calcular as estatísticas do conjunto inteiro, cada ponto é a estatística (média, desvio, variância, etc) dos pontos da “janela” anterior.
janela é um subconjunto de observações seguidas
mediamovel = df['meantemp'].rolling(window=7).mean()
#window = 7 diz que a janela usada para média móvel é de 7 observações (no caso 7 dias)
desviomovel = df['meantemp'].rolling(window=7).std()
orig = plt.plot(df['meantemp'], color='blue', label='Observado')
media = plt.plot(mediamovel, color='red', label='Média Móvel')
desvio = plt.plot(desviomovel, color='black', label='Desvio Padrão Móvel')
plt.legend(loc='best')
plt.title('Estatísticas de rolagem')
plt.show(block=False)
Com essa imagem conseguimos ter uma noção que a série não é estacionária, mas para termos certeza existe um teste estatístico chamado Augmented Dickey–Fuller (ADCF). O teste considera como hipótese nula a não estacionariedade e como hipótese alternativa a estacionariedade. Para interpretar o teste podemos olhar para o p-valor que tem ser menor do que o nível de significância escolhido e o valor do teste tem que ser menor que o valor crítico para esse mesmo nível de significância.
from statsmodels.tsa.stattools import adfuller
adftest = adfuller(df['meantemp'])#Para printar os resultados de maneira elegante:
out = pd.Series(adftest[0:4], index=['Teste','p-valor','Lags','Número de observações usadas'])
for key,value in adftest[4].items():
out['Valor crítico (%s)'%key] = value
print(out)
Teste -1.096474
p-valor 0.716476
Lags 0.000000
Número de observações usadas 113.000000
Valor crítico (10%) -2.580604
Valor crítico (5%) -2.887477
Valor crítico (1%) -3.489590
Como podemos ver essa série não é estacionária ainda. Pensando num nível de significância de 5%, o p-valor e o valor do teste estão muito altos.
Como deixar uma série estacionária?
Podemos aplicar algumas técnicas nos dados para conseguir uma série estacionária, como exemplo, transformações (logarítmica, a raiz quadrada, boxcox), diferenciação, etc.
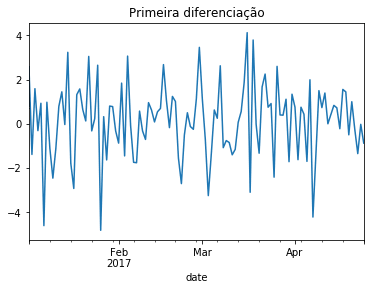
O primeiro método que vou tentar é a diferenciação. Esse processo cria uma nova série a partir da diferença de uma observação com a observação anterior.
diff(t) = obs(t) - obs(t-1)
Através da diferenciação também é possível remover a dependência temporal de uma série, reduzindo a tendência e a sazonalidade. Por esse motivo esse método pode ser usado para atingir a estacionariedade. Pode-se diferenciar uma série mais de uma vez, caso seja necessário para remover a dependência.
dfdiff = df.meantemp.diff()
dfdiff = dfdiff.dropna()
dfdiff.plot()
E aplicando o ADCF teste temos:
Teste -1.203580e+01
p-valor 2.805321e-22
Lags 0.000000e+00
Número de observações usadas 1.120000e+02
Valor Crítico (10%) -2.580730e+00
Valor Crítico (5%) -2.887712e+00
Valor Crítico (1%) -3.490131e+00
Com esses valores já teríamos uma série estacionária, considerando um nível de significância de 5%, e já daria para prosseguir com outras análises.
O segundo método que vou usar é a transformação de Box-cox. Essa transformação tem como objetivo deixar os dados mais normalizados e consequentemente estabiliza a variância durante os dados. A sua função tem apenas um parâmetro, lambda, que denota como será feita essa transformação, podemos definir esse valor ou deixar a função achar “o melhor valor”.
from scipy.stats import boxcox
meantemp_bcx, lam = boxcox(df['meantemp'])
print('Lambda: %f' % lam)
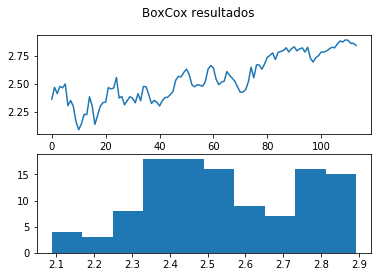
fig, ax = plt.subplots()
fig.suptitle("BoxCox resultados")
# line plot
plt.subplot(211)
plt.plot(meantemp_bcx)
# histogram
plt.subplot(212)
plt.hist(meantemp_bcx)
plt.show()
#resultado:
Lambda: -0.118270
Olhando para o gráfico e para o resultado do teste abaixo vemos que esse método não foi muito eficaz para conseguir a estacionariedade.
Teste -1.444017
p-valor 0.561001
Lags 0.000000
Número de observações usadas 113.000000
Valor Crítico (1%) -3.489590
Valor Crítico (5%) -2.887477
Valor Crítico (10%) -2.580604
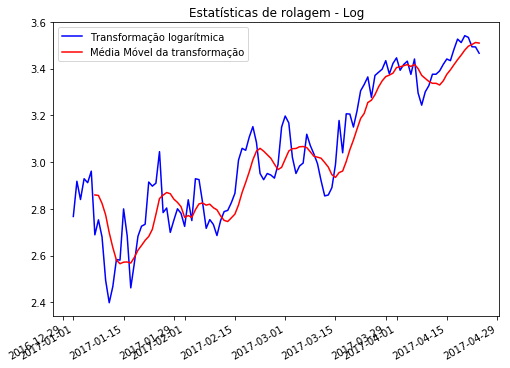
Seguindo para o último método, vou tentar também uma abordagem bem legal que vi em uma das referências que usei para estudar. Vou fazer uma transformação logarítmica e subtrair a média móvel dos dados transformados. O gráfico abaixo mostra as duas séries comparadas.
temp_log = np.log(df['meantemp']) #Transformação logarítmica
log_menos_media = temp_log - mediamovel_log
log_menos_media.dropna(inplace=True)
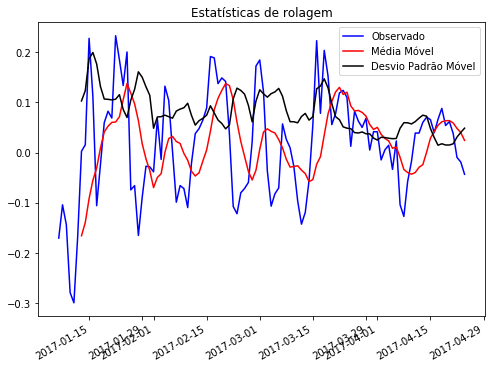
Estatísticas de rolagem referentes a série “log_menos_media”
Teste -5.988135e+00
p-valor 1.771911e-07
Lags 3.000000e+00
Número de observações usadas 1.040000e+02
Valor Crítico (1%) -3.494850e+00
Valor Crítico (5%) -2.889758e+00
Valor Crítico (10%) -2.581822e+00
Conseguimos uma série estacionária \o/, mas por que deu certo?
Quando plotamos a média móvel dessa série e a série transformada é possível ver nos dois casos que existe uma tendência nos dados. A teoria era que subtraindo as duas essa tendência fosse perdida e sobraria apenas as partes estacionárias da série final.
MM = tendênciaM + estacionariedadeM
TL = tendênciaL + estacionariedadeL
TL-MM = (tendênciaL + estacionariedadeL)-(tendênciaM + estacionariedadeM) = tendênciaL - tendênciaM + estacionariedadeL - estacionariedadeM
Referências e sugestões:
Link para o código completo do artigo
Everything you can do with a time series
Time Series for beginners with ARIMA
Análise de séries temporais — UFSC : Explica decomposição em detalhes e em português!





Top comments (0)