When you code in a low-level language like C, you worry about picking the right data type and qualifiers for your integers; at every step, you need to think if int would suffice or should you go for a long or even higher to a long double. But while coding in python, you need not worry about these "trivial" things because python supports integers of arbitrary size.
In C, when you try to compute 2²⁰⁰⁰⁰ using builtin powl function it gives you inf as the output.
#include <stdio.h>
#include <math.h>
int main(void) {
printf("%Lf\n", powl(2, 20000));
return 0;
}
$ ./a.out
inf
But for python, it is a piece of cake 🎂
>>> 2 ** 20000
39802768403379665923543072061912024537047727804924259387134 ...
...
... 6021 digits long ...
...
6309376
Python must be doing something beautiful internally to support integers of arbitrary sizes and today we find out what's under the hood!
Representation and definition
An integer in Python is a C struct defined as following
struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};
PyObject_VAR_HEAD is a macro that expands into a PyVarObject that has the following structure
typedef struct {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
Other types that has PyObject_VAR_HEAD are
PyBytesObjectPyTupleObjectPyListObject
This indicates that an integer, just like a tuple or a list, is variable in length and this is our first insight into how it could support gigantically long integers. The _longobject after macro expansion could be roughly seen as
struct _longobject {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
digit ob_digit[1];
};
These are some meta fields in the
PyObjectstruct, used for reference counting (garbage collection), but that we would require a separate article. The field that we will focus on isob_digitand to some extentob_size.
Decoding ob_digit
ob_digit is an array of type digit, typedef'ed from uint32_t, statically allocated to length 1. Since it is an array, ob_digit primarily is a digit *, pointer to digit, and hence if required could be malloced to any length. This makes it possible for python to represent and handle gigantically long integers.
Generally, In low-level languages like C, the precision of integers is limited to 64-bit, but Python implements Arbitrary-precision integers. Since Python 3 all integers are represented as a bignum and these are limited only by the available memory of the host system.
Decoding ob_size
ob_size holds the count of elements in ob_digit. To be more efficient while allocating the memory to array ob_digit, python over-provisions and then relies on the value of ob_size to determine the actual number of elements held int the array.
Storage
A naive way to store an integer digit-wise is by actually storing a decimal digit in one item of the array and then operations like addition and subtraction could be performed just like grade school mathematics.
With this approach, a number 5238 will be stored as
This approach is inefficient as we will be using up 32 bits of digit (uint32_t) to store a decimal digit that actually ranges only from 0 to 9 and could have been easily represented by mere 4 bits, and while writing something as versatile as python, a core developer has to be more resourceful than this.
So, can we do better? for sure, otherwise, this article should hold no place on the internet. Let's dive into how python stores a super long integer.
The pythonic way
Instead of storing just one decimal digit in each item of the array ob_digit, python converts the number from base 10 to base 2³⁰ and calls each of element as digit which ranges from 0 to 2³⁰ - 1.
In the hexadecimal number system, the base is 16 ~ 2⁴ this means each "digit" of a hexadecimal number ranges from 0 to 15 of the decimal system. Similarly for python, "digit" is in base 2³⁰ which means it will range from 0 to 2³⁰ - 1 = 1073741823 of the decimal system.
This way python efficiently uses almost all of the allocated space of 32 bits per digit and keeps itself resourceful and still performs operations such as addition and subtraction like grade school mathematics.
Depending on the platform, Python uses either 32-bit unsigned integer arrays with 30-bit digits or 16-bit unsigned integer arrays with 15-bit digits. It requires a couple of bits to perform operations that will be discussed in some future articles.
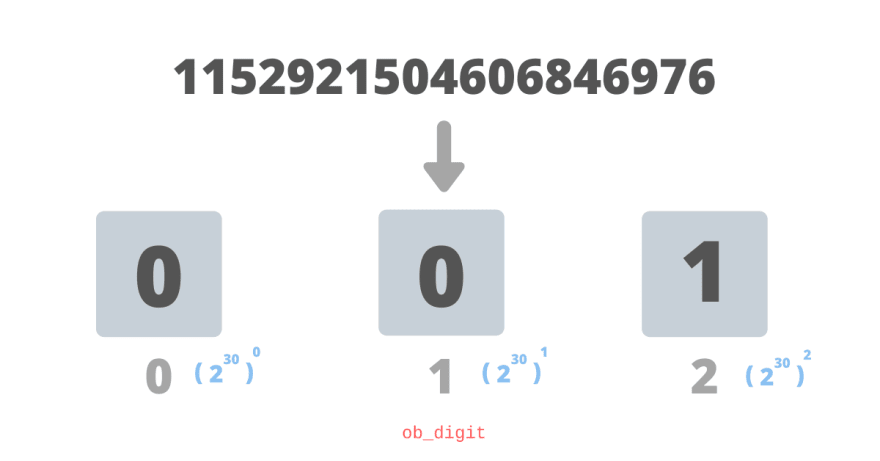
Example: 1152921504606846976
As mentioned, for Python a "digit" is base 2³⁰ hence if you convert 1152921504606846976 into base 2³⁰ you get 100.
1152921504606846976 = 1 * (2³⁰)² + 0 * (2³⁰)¹ + 0 * (2³⁰)⁰
Since ob_digit persists it least significant digit first, it gets stored as 001 in 3 different digits.
The _longobject struct for this value will hold
-
ob_sizeas3 -
ob_digitas[0, 0, 1]
I have created a demo REPL that will output the way python is storing integers internally and also has reference to struct members like ob_size, ob_refcount, etc.
Operations on super long integers
Now that we have a fair idea on how python supports and implements arbitrary precision integers its time to understand how various mathematical operations happen on them.
Addition
Integers are persisted "digit-wise", this means the addition is as simple as what we learned in the grade school and python's source code shows us that this is exactly how it is implemented as well. The function named x_add in file longobject.c performs the addition of two numbers.
...
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
z->ob_digit[i] = carry;
...
The code snippet above is taken from x_add function and you could see that it iterates over the digits and performs addition digit-wise and computes and propagates carry.
Things become interesting when the result of the addition is a negative number. The sign of
ob_sizeis the sign of the integer, which means, if you have a negative number thenob_sizewill be negative. The absolute value ofob_sizewill determine the number of digits inob_digit.
Subtraction
Similar to how addition is implemented, subtraction also happens digit-wise. The function named x_sub in file longobject.c performs subtraction of two numbers.
...
for (i = 0; i < size_b; ++i) {
borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
z->ob_digit[i] = borrow & PyLong_MASK;
borrow >>= PyLong_SHIFT;
borrow &= 1; /* Keep only one sign bit */
}
for (; i < size_a; ++i) {
borrow = a->ob_digit[i] - borrow;
z->ob_digit[i] = borrow & PyLong_MASK;
borrow >>= PyLong_SHIFT;
borrow &= 1; /* Keep only one sign bit */
}
...
The code snippet above is taken from x_sub function and you could see how it iterates over the digits and performs subtraction and computes and propagates burrow. Very similar to addition indeed.
Multiplication
Again a naive way to implement multiplication will be what we learned in grade school math but it won't be very efficient. Python, in order to keep things efficient implements the Karatsuba algorithm that multiplies two n-digit numbers in O ( nˡᵒᵍ³ ) elementary steps.
The algorithm is slightly complicated is out of the scope of this article but you can find its implementation in k_mul and
k_lopsided_mul functions in file longobject.c.
Division and other operations
All operations on integers are defined in the file longobject.c and it is very simple to locate and trace each one. Warning: it will take some time to understand each one in detail so grab some popcorn before you start skimming.
Optimization of commonly-used integers
Python preallocates small integers in a range of -5 to 256. This allocation happens during initialization and since we cannot update integers (immutability) these preallocated integers are singletons and are directly referenced instead of reallocating. This means every time we use/creates a small integer, python instead of reallocating just returns the reference of preallocated one.
This optimization can be traced in the macro IS_SMALL_INT and the function get_small_int in longobject.c. This way python saves a lot of space and computation for commonly used integers.
This is the second article in the Python Internals series. The first article was How I changed my Python and made it dubious and it helps you take your first steps in Python's source code and paves the way for you to become a Python Core Developer.
This article was originally published on my blog - How python implements super long integers?.
If you want to read more articles like this, subscribe to my newsletter and get the post delivered directly to your inbox. I write about Engineering, System Design and a bit of programming, every Friday. Give me a shout-out @arpit_bhayani. You can find my previous articles @arpitbhayani.me/blogs.




Top comments (0)