In the previous post, I discussed applying Principal Component Analysis (PCA) as a way to reduce feature space, by capturing maximum variance. So, why is variance a big deal? If there is no or little variation, it means we are not getting enough predictive information from the feature.
Here, I wanted to experiment with covariance and correlation matrices and try to derive principal components using linear algebra. I will use the London bike sharing dataset from my previous blog.
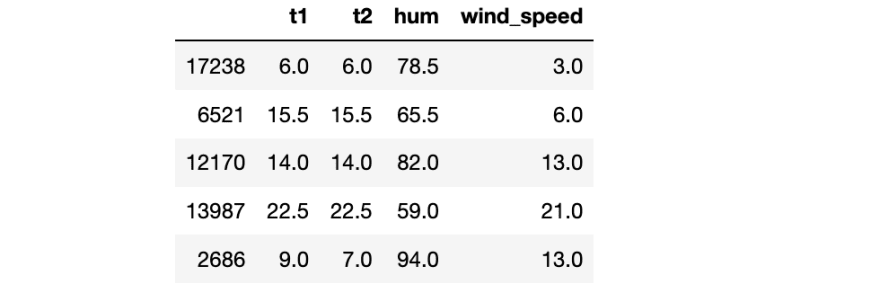
### use 4 features
features = data.iloc[:,:4]
features.sample(5)
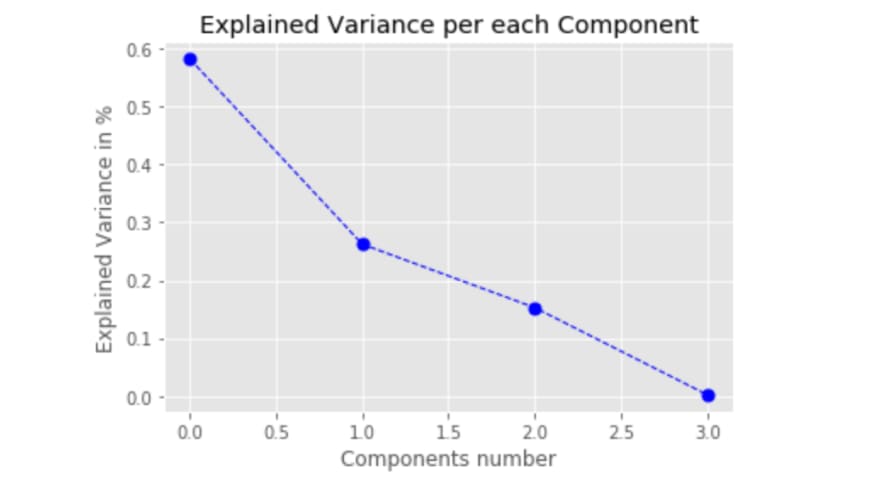
So, the idea is to find eigenvalues and eigenvectors of the correlation matrix. Then, we can use eigenvalues to describe the explained variation ratio.
Let’s start with the correlation matrix. We can use either original features or standardized for correlation matrix calculation, as it gives the same result.
from sklearn.preprocessing import StandardScaler
# standardize features
features_scaled = StandardScaler().fit_transform(features)
# get correlation matrix on scaled features
np.corrcoef(features_scaled.T)
# correlation matrix on unscaled data gives the same result
# features.corr()
e_vals, e_vects = np.linalg.eig(np.corrcoef(features_scaled.T))
# normalize eigenvalues to get variations for each PC
# sorted explained variation
# use np.sort(e_val)[::-1] to sort in descending order
print([x/e_vals.sum() for x in np.sort(e_vals)[::-1]])
We could do the same using the covariance matrix, but it requires a few more extra matrix manipulations before getting eigenvalues. You can find the code here.
Let's check if we get the same result using sklearn’s PCA. I would like to mention that per sklearn documentation, it uses SVD decomposition instead of eigendecomposition as we did above and we also need to standardize the data.
# Use sklearn's PCA
from sklearn.decomposition import PCA
pca = PCA()
#fit and transform scaled features
pca.fit_transform(features_scaled)
# get explained varion ratio
print(pca.explained_variance_ratio_)
As we can see, we got the same variance ratio. Based on that analysis, we can further decide how many principal components we would use and accordingly apply the projection matrix or sklearn to transform features into principal components.









Top comments (0)