No meu artigo anterior, falei sobre o que são os 0's e 1's no mundo da computação.
Para entender como conseguimos representar dados mais complexos a partir de 0's e 1's, é necessário entender sobre sistemas de numeração e representação numérica.
Sistemas de representação numérica
Estamos acostumados com o sistema de numeração decimal (isto é, sistema de base 10). Representamos números combinando 10 possíveis símbolos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) de modo a representar quantidades. Mas este não é o único jeito.
O sistema de numeração binário (ou sistema de base 2) é usado para representar quantidades com apenas dois símbolos: 0 e 1.
Assim como no sistema decimal, podemos combinar 0's e 1's:
- 10 em binário representa 2 em decimal;
- 11 representa 3;
- 100 representa 4;
- e daí por diante.
Outros sistemas comumente utilizados no mundo da computação são os sistemas octal (base 8) e hexadecimal (base 16).
No sistema octal, formamos números utilizando apenas os símbolos de 0 a 7.
No sistema hexadecimal, além de 0 a 9, utilizamos A, B, C, D, E e F.
| Decimal | Binário | Octal | Hexadecimal |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Dígitos e seus pesos
No sistema decimal, os dígitos de um número podem ser classificados como unidade, dezena, centena... Essas nomenclaturas estão associadas a pesos.
Um dígito de dezena possui um peso 10 vezes maior que um dígito de unidade; um dígito de centena, 10 vezes maior que o de dezena; e assim vai.
Do mesmo modo, no sistema binário, cada dígito tem um peso.
Geralmente o bit mais à esquerda é chamado de Bit Mais Significativo (Most Significant Bit, MSB), e o bit mais à direita, Bit Menos Significativo (Least Significant Bit, LSB).
Agrupando bits e representando números
Na computação, chamamos os símbolos binários de bits (o termo bit é a abreviação de binary digit, ou dígito binário, em português). Geralmente, os bits são agrupados em unidades maiores, por exemplo:
- 1 nibble = 4 bits;
- 1 byte = 8 bits;
- 1 word = 16 bits.
Geralmente, o byte é tomado como unidade de medida para quantificar o tamanho de arquivos, velocidade de upload/download e etc.
Com 1 byte, podemos representar 256 valores diferentes.
Motivo:
- Um bit pode assumir 2 valores possíveis (0 ou 1);
- Um byte é um grupo de 8 bits;
- Logo, podemos representar 2⁸ = 256 combinações diferentes.
"Ah, mas e quanto a valores maiores que 255?"
Podemos agrupar bytes para formar tipos de dados que representam uma faixa maior de valores.
No mundo da programação nos dias de hoje, é comum utilizar tipos de dados inteiros de 32 bits e 64 bits, capazes de representar valores BEEEEEM maiores.
Representação de números negativos
Se a gente for traduzir do binário para o decimal, com 1 byte podemos representar quantidades inteiras de 0 a 255.
Mas e se a gente precisar representar números negativos?
Bom, no geral, as duas maneiras mais conhecidas para isso são a representação sinal-magnitude e a representação complemento de 2 (esta última mais usada).
Números negativos: Formato Sinal-Magnitude
Considerando um grupo de bits, podemos reservar o MSB para representar um sinal.
Neste caso, 0 representa sinal positivo; 1 representa sinal negativo.
Na representação Sinal-Magnitude, a parte que representa o valor numérico permanece igual na representação positiva e na negativa.
Números negativos: Formato Complemento de 2
Na representação por Complemento de 2, também reservamos o MSB para representar o sinal. No entanto, a parte que representa o valor muda.
Para obter a parte que representa o valor, nós invertemos todos os bits (o que é 0 vira 1 e vice-versa), e depois somamos 1 ao valor invertido.
"Ah, mas por que Complemento de 2 é mais usado que Sinal-Magnitude?"
A representação em Complemento de 2 é mais eficiente para operações aritméticas, como por exemplo a subtração.
Representação de números não-inteiros
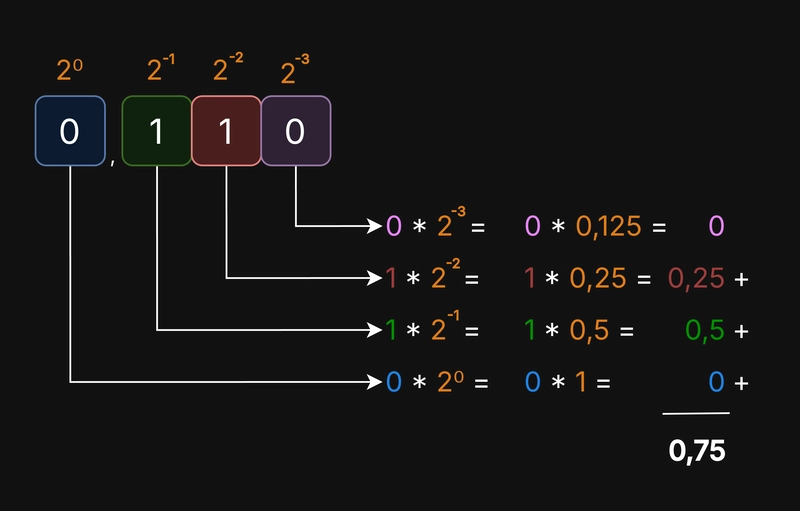
Assim como podemos representar números inteiros com o sistema de numeração binário, também podemos representar partes não-inteiras.
As partes não-inteiras tem pesos com expoentes negativos, levando à geração de valores não-inteiros.
No geral, os dois formatos de representação mais comuns para números não-inteiros são:
- Ponto Fixo;
- Ponto Flutuante.
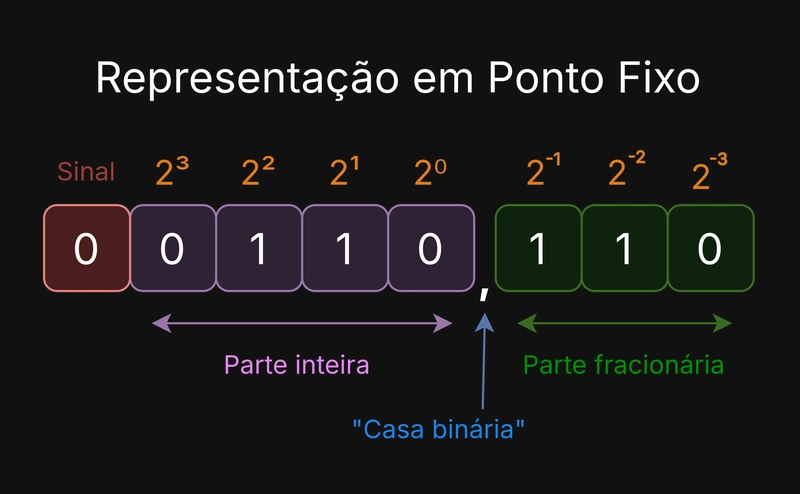
Números não-inteiros: Ponto Fixo
A representação em Ponto Fixo estabelece que, dado um conjunto de bits, o ponto de separação (que a gente geralmente chama de "casa decimal") é fixado em uma determinada posição.
O Ponto Fixo pode ter suas partes inteira e fracionária dimensionadas de várias formas.
Um determinado valor representado em Ponto Fixo Qm.n possui:
- 1 bit reservado para sinal;
- m bits reservados para a parte inteira;
- n bits reservados para a parte fracionária.
Vantagens da representação em ponto fixo:
- Eficiência computacional;
- Recomendado para uso em ambientes com poder de computação limitado;
- Os mesmos circuitos para aritmética de números inteiros podem ser usados para cálculos com números de ponto fixo.
Desvantagens da representação em ponto fixo:
- Falta de flexibilidade e precisão limitada na representação da parte fracionária;
- Erros significativos de arredondamento/truncamento.
Pensando nas desvantagens, a IEEE produziu o Padrão IEEE-754 para representação de números em Ponto Flutuante.
Números não-inteiros: Ponto Flutuante
Na representação convencional em Ponto Flutuante definida pelo Padrão IEEE-754, podemos ter precisão simples (32 bits) ou dupla (64 bits) para representar um número.
Num número em ponto flutuante, são definidas 3 partes principais:
- Sinal;
- Expoente;
- Mantissa.
Mas para que essas partes servem?
No geral, para recuperar um número a partir da representação em ponto flutuante, calculamos a seguinte fórmula:
- N = Número;
- S = Sinal;
- E = Expoente;
- M = Mantissa.
Mas como se chegou a essa fórmula?
Primeiro, vamos entender a parte do sinal.
Calculando , obtemos o fator multiplicador que atribui o sinal positivo ou negativo ao número.
Caso S = 0, o fator multiplicador é 1. Caso S = 1, o fator é -1.
Quanto ao expoente e a mantissa:
A mantissa carrega o valor numérico.
O expoente determina a posição da casa que irá dividir a representação binária em parte inteira e parte fracionária.
Chamamos esta representação de Ponto Flutuante porque, por meio dela, podemos reposicionar a "casa" de modo dinâmico, e assim, conseguimos algumas vantagens:
- Maior precisão (comparada com o ponto fixo);
- Maior flexibilidade no posicionamento da casa;
- Pode representar uma faixa maior de valores.
Quanto às desvantagens do ponto flutuante, temos:
- Maior complexidade para operações aritméticas;
- Representação não é totalmente imune a erros de arredondamento/truncamento (ainda assim, os erros estão dentro do limite do aceitável).
A complexidade e a velocidade das operações aritméticas com números em ponto flutuante não chega a ser uma preocupação tão grande hoje em dia.
Os processadores e microcontroladores modernos já contam com estruturas dedicadas e otimizadas para operações com ponto flutuante.



















Top comments (2)
Super didatico, simplificou muito. Muito obrigada :)
Obrigado por partilhar seu conhecimento 💙