Você já deve ter ouvido por aí que o computador "só entende 0's e 1's". Mas de onde vem esses 0's e 1's? O que eles representam?
Analógico vs. Digital
Antigamente, os sistemas eletrônicos lidavam com a informação de forma analógica, ou seja, os sinais elétricos que representavam a informação podiam assumir uma infinidade de amplitudes de tensão.
Exemplo: Rádio AM, Rádio FM, TV Analógica.
Todos os sistemas são suscetíveis a ruído, e para informação representada de modo analógico, isto é um grande problema, pois o processamento de sinais analógicos depende de alta precisão na amplitude, a qual é bastante afetada pelo ruído.
Fonte: https://www.predig.com/whitepaper/reducing-signal-noise-practice
A codificação digital veio como uma forma de reduzir erros decorrentes do ruído, e para isso, a informação é representada apenas em regiões de tensão bem definidas.
(Isso não significa que sistemas digitais são totalmente imunes a erros.)
Fonte: https://www.predig.com/whitepaper/reducing-signal-noise-practice
Sinal digital
No geral, um sinal digital pode assumir dois níveis de tensão:
- 0 V, ao qual atribuímos o valor lógico 0;
- 5 V / 3,3 V / 1,8 V / etc. (dependendo da tecnologia de implementação), ao qual é atribuído o valor lógico 1.
Em computação, o "valor lógico" é chamado de bit (abreviação de binary digit, ou dígito binário).
Todos aqueles 0's e 1's dos quais você ouve falar são representados fisicamente pelo fluxo de sinais elétricos, os quais são controlados por meio de dispositivos eletrônicos.
Transistores e Portas Lógicas
Em circuitos digitais modernos, os dispositivos utilizados para controlar tais sinais são os transistores.
Transistores são compostos de materiais semicondutores dispostos de maneira inteligente, de modo que podem ser utilizados como chaveadores.
"Ah, mas como assim chaveadores?"
Pense em um interruptor de lâmpada: podemos LIGÁ-LO ou DESLIGÁ-LO.
Do mesmo modo, o transistor pode ser controlado para permitir ou bloquear a passagem de corrente elétrica.
Os transistores são utilizados para construir arranjos levemente mais complexos, aos quais chamamos de "portas lógicas".
Tais componentes recebem sinais digitais de entrada e retornam um sinal digital como saída, executando uma operação lógica.
Antes de partir para as portas lógicas:
Assim como chamamos os dois estados de um interruptor de LIGADO e DESLIGADO, também podemos atribuir significado ao 1 e ao 0, aos quais geralmente chamamos de TRUE e FALSE (VERDADEIRO e FALSO), respectivamente.
Porta lógica AND
A porta lógica AND (em português, E) recebe várias entradas e retorna uma saída.
Tal porta retorna verdadeiro (1) se todas as entradas são verdadeiras (1) ao mesmo tempo; caso contrário, ela retorna falso (0).
Q = A e B
Porta lógica OR
A porta OR (OU) funciona de outra forma:
Dentre as várias entradas, basta que pelo menos uma delas seja verdadeira (1) para que a saída seja verdadeira (1)
Q = A ou B
Porta lógica XOR
A porta XOR (OU EXCLUSIVO) funciona de forma diferente: Dadas duas entradas, apenas uma das duas deve receber um sinal verdadeiro (1) para que a saída seja verdadeira (1), o que significa: OU A, OU B (A E B ao mesmo tempo retorna 0)
Q = ou A, ou B
Porta lógica NOT
A porta NOT (NÃO) recebe apenas uma entrada, e como o próprio nome diz, o estado lógico da entrada é invertido na saída
Q = não A
Porta lógica NAND
A porta NAND (NÃO E) é literalmente o contrário da porta AND: só sai falso (0) se todas as entradas forem verdadeiras (1) ao mesmo tempo. É basicamente a mesma coisa que pegar uma porta AND e colocar uma porta NOT na saída.
Q = não (A e B)
Porta lógica NOR
Do mesmo modo, a porta NOR (NÃO OU) é o contrário da porta OU: basta que pelo menos uma das entradas seja verdadeira (1) para que a porta retorne falso (0). É basicamente a mesma coisa que pegar uma porta OR e colocar uma porta NOT na saída.
Q = não (A ou B)
Porta lógica XNOR
A porta XNOR (NÃO OU EXCLUSIVO) também é chamada de "porta coincidência", pois ela retorna verdadeiro (1) se suas duas entradas forem iguais. É a mesma coisa de pegar uma porta XOR e colocar uma porta NOT na frente.
Q = não (ou A, ou B)
Paralelo entre portas lógicas e programação
Em programação, podemos pensar nos laços condicionais como "aplicações de portas lógicas".
Geralmente, quando programamos um if, estabelecemos condições para que um determinado bloco de código seja executado. Cada condição pode ser pensada como um bit (0 se for falsa, 1 se for verdadeira). Podemos fazer operações com esses bits, como se estivéssemos usando portas lógicas. Na maioria das linguagens de programação, podemos usar os operadores &&, || e ! para as operações AND, OR e NOT, respectivamente. Estes operadores são chamados de operadores lógicos.
Para além das condicionais, podemos utilizar operações correlatas às portas lógicas para comparar números bit a bit por meio dos operadores bitwise. Para tratar deste assunto com mais profundidade, é necessário entender melhor sobre sistemas de numeração (explico sobre esse assunto neste artigo aqui).
Associações de portas lógicas
Portas lógicas podem ser associadas e conectadas entre si para formar circuitos mais complexos. No geral, é possível construir dois tipos de circuitos:
- Circuitos combinacionais, que propagam os sinais de entrada pelas portas lógicas até a saída, sem realimentação;
- Circuitos sequenciais, que possuem realimentação arranjada de forma inteligente, formando as peças básicas que constituem o que conhecemos como memória.
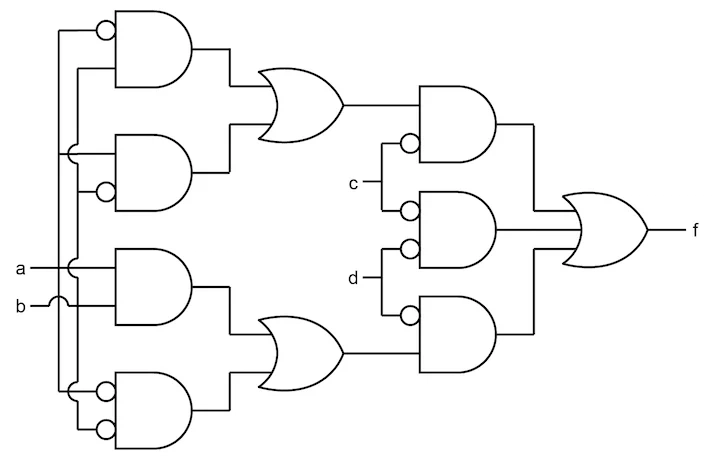
Um exemplo de circuito combinacional é o circuito da imagem abaixo (as bolinhas nas entradas representam portas NOT). Os circuitos sequenciais provavelmente serão tratados em um futuro artigo.
Álgebra Booleana
Além de diagramas, podemos representar os circuitos combinacionais como expressões algébricas, com base na Álgebra Booleana.
A álgebra booleana foi criada por George Boole, um matemático inglês, durante o século XIX. Com o tempo, o trabalho de Boole se provou útil para representar algebricamente as possíveis relações e operações envolvendo informações binárias.
Representando as portas lógicas por meio da álgebra booleana:
| Porta lógica | Expressão algébrica |
|---|---|
| NOT | , ou |
| AND | |
| NAND | , ou |
| OR | |
| NOR | , ou |
| XOR | |
| XNOR |
Assim como em expressões aritméticas, expressões booleanas também possuem suas propriedades de operação, algumas delas representadas abaixo.
Bilhões de portas lógicas!
Circuitos integrados, ou chips, como são popularmente conhecidos, costumam conter circuitos muito mais complexos e com bilhões de transistores formando um incrível número de portas lógicas, arranjadas de modo inteligente para executar várias funções.
Tomemos como exemplo processadores de computador e de smartphone: várias portas lógicas são arranjadas para formar a Unidade Lógica e Aritmética (ULA), a qual é responsável por efetuar operações matemáticas; Registradores, que guardam temporariamente dados que são utilizados para executar instruções; a Unidade de Controle, que é responsável por disparar os sinais elétricos responsáveis por gerenciar o fluxo de dados no processador e comunicação do processador com periféricos; dentre outras funcionalidades.
Caso tenha curiosidade em entender melhor como é o processo de fabricação de microchips, recomendo o seguinte vídeo:























Top comments (1)
Ótimo material, @xornotor! Muito interessante e enriquecedor, principalmente para quem está começando a se interessar pela área da computação. Ansioso pelos próximos artigos!