Monty Hall Problem is a famous probability puzzle in statistics. It is named after Monty, the host of the television game show "Let's Makes a Deal". The brain teaser loosely replicates the game show concept and it goes like this:
There are 3 doors. You will have to choose a door, and you will win whatever behind it. There is one door with a car. Each remaining door has a goat. First, you are asked to pick one of the doors. Next, Monty, who knows what's behind each of the doors, opens up one of the two doors you didn’t pick and reveal a goat. Finally, you are given the opportunity to either “stay” with your original choice, or “switch” to the remaining door. What is the best strategy to win the car?
I first encountered this problem 4 years ago in a statistics class. It was hard enough that I spent the whole day thinking about it and still insist on 1/2 for both strategies. My explanation was: there are 3 doors, 1 door has a car. If the host opens one door that has the goat, one out of two remaining doors must have the car. So regardless of "switching" or "staying", the probability should be 1/2!
I was wrong. The tricky part of this problem is Monty knows what behind those doors so his decision has an influence on the outcome. Take a minute for yourself to think if this is true.
1) Intuitive answer
Assuming that the three doors are: 1, 2, and 3
Since probability = Event/Sample space we just need to find these variable and plug in the equation.
Sample space here is the total of different ways that we choose the door and where the car actually is. There are 6 possibilities which are illustrated in the following table:
Note that in this table, Monty has already eliminated the door with the goat.
As you can see, the probability of winning for "staying" strategy is 1/3 while "switching" is 2/3.
2) Bayes formula method
This is another approach for people who loves Bayes!
Let P(A|B) denote the probability of event A given that event B already happened
If we know how to translate the problem into events, then everything becomes straight forward. Let:
- A be the event that is choosing the door with the car on the first choice.
- B be the event that Monty eliminates one door that has a goat. So we are looking for P(A|B), the "staying" strategy.
Let write down things that we know:
- P(B|A) = 1, since Monty always choose the right door regardless of any given condition
- P(A) =1/3, there is a 1/3 chance of opening the car door, without knowing anything.
-
To understand how to find P(B), let's look at the diagram:
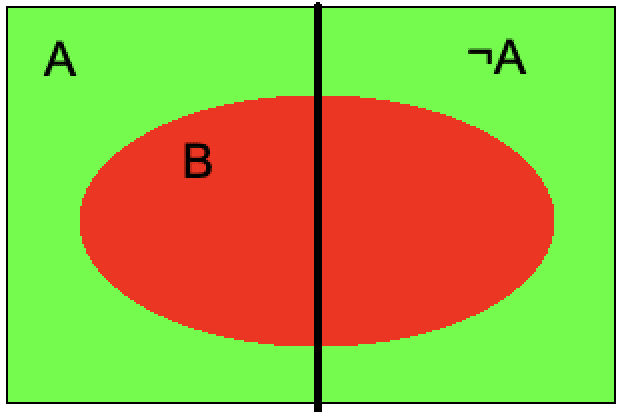
There are only 2 possible strategies, either stay or switch. Thus, "switching" probability is the complement of staying, which is 1-1/3=2/3.
If Monty does not know which door has the goat. This is equivalent to P(B|A)=1 and P(B|¬A)=1/2. Plug them back to the equation and it returns P(B|A)=1/2. This is the part that I was confused.
3) Simpler answer
With the "staying" strategy, you can only win if you choose the door with a car at first. Since there are 3 doors, the probability of choosing a door with a car is 1/3. So the "switching" strategy is 2/3. This provide us a general observation for more than 3 doors Monty Hall problem.
4) What if?
What if Monty Hall decides to reveal k doors out of n doors where the maximum number of k is n-2, will it affect the strategy at all?
"Switching" in this case means not keeping the original choice
Case A: k=n-2
This case is similar to the original problem. Note that you cannot switch to the door that you chose. So "Staying" win rate is always 1/n and switching win rate, in this case, is (n-1)/n
Case B: k<n-2
The probability of choosing the door with a car at the beginning is still 1/n. Thus "staying" = 1/n
In the "switching" strategy, your final choice cannot be your first choice. Thus, you don't want to choose the first door which has the car at the beginning. The probability of not choosing it is (n-1)/n. The k-th switch is also when your pick, there are n-k door(s) left but you must exclude your first door. Thus, the probability of picking the prized door in the last step is 1/(n-k-1). Together we have:
It shows that the "switching" strategy is always better than "staying" strategy.
5) Simulation
Let run it on python to see if our formula work. Let n be the number of doors and r is the number of door Monty wants to reveal
The graph shows that the statistical result getting close to our actual answer when increasing the number of iteration.
So, you know what you should do if you play a similar game like this next time.
For more information about the code, please visit my Githup repository.





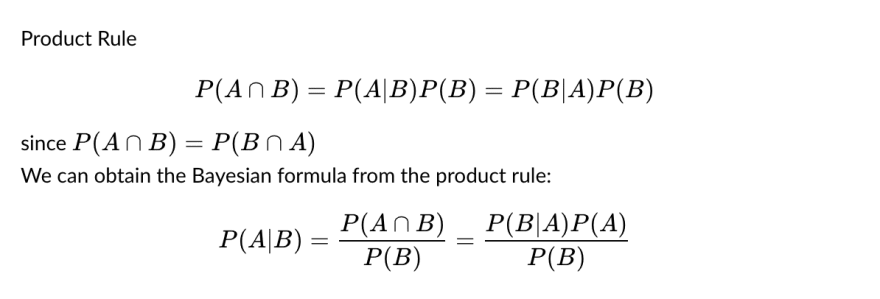
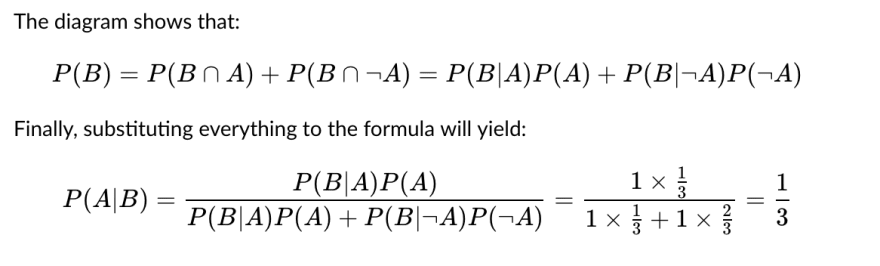




Top comments (10)
Great explanation!
I think the
kdoors case is the best way to develop an intuition for the problem.Suppose there were 100 doors, you choose one. Then Monty goes ahead and opens 98 non-winning doors from the remaining 99, leaving one door unopened. I think the decision to switch makes more intuitive sense here, and then you can see that the intuition still applies when you scale back to 3 doors.
You are right! Since he never chooses that winning door so we increase our belief that is the one every time he opens the new door.
lol - I had a day-long argument with an ex-girlfriend about this. She insisted that it was a 1 in 2 chance of making the right choice after one door is opened and I was adamant it was 2 in 3. For once I was right :)
Anyway - it's a really good example of how people's intuition around statistics can be completely wrong. Same as the fact that one roll of a dice is never going to affect the outcome of the next...
Thank you. You can use my blog post as part of your explanation next time you see her. :D
I first learned of this problem about ten years ago and one of my hobbies for a while was "arguing" about it over a few drinks with my brother until he finally saw the light. I believe it was the hundred doors variant that finally got him to understand.
It's a strange coincidence that you posted this - I just wrote a Monty Hall Problem simulator on Thursday to get some Java practice in before my new job starts next week. It runs through a million iterations and gets a consistent 67% wins when switching doors.
I was really excited when my simulation result matches the exact result. This stuff is fun!
This is interesting: "This 'equal probability' assumption is a deeply rooted intuition (Falk 1992:202)"..."The problem continues to attract the attention of cognitive psychologists".
I actually had to wrap my mind around to find a good way to make sense of the "switching" strategy in the (n,k) version. Once my simulation worked, I gained some intuition and understood more about the original version.
It is weird how the brain works but it is good to know that I am not alone.
I'm sorry to point this out, but there is an error in your Bayesian formula.
(1/3)/(1/3+2/3) is 1/3 and not 2/3.
I'm not exactly sure where the error is.
I fixed it. Thank you!
written a python simulation when I was introduced to this and funny how true it was.