Just to be clear, by delimiters I mean mathematical delimiters - parentheses, braces, and brackets. Also this post will be discussing code from a java class I wrote to be used as a library. You can check the repo here. Alright, with that out of the way, let's go!

Part 1 - Auto-complete

Introduction

A few months ago I needed to have an auto-complete delimiters function in one of my programs. I never really thought about how to do it because it's really not something that just occurs. I mean like, have you ever manually went step by step thinking how to match that one open brace that you didn't close in your program yet? No, you just know instinctively. Your brain is just incredibly good at detecting and matching patterns. But a program doesn't have instincts. So, what's the algorithm behind this pattern matching? How does the brain do it, step by step?

Before I start the explanation, I highly recommend you check out the code on github and follow along! Feel free to import the class if you ever need it in the future :)

The Algorithm

Well, just check the number of opening delimiters (i.e (, { and [) in an expression and put that number of closing delimiters at the end! So if you were given log(sin(2^(5 you'd just put 3 closing parentheses in the end, right?

Not so fast. What if the expression is log(sin(2^(5)? You can't put 3 closing delimiters now, you have to put 2, because 1 is already closed. So we can't just count the appearance of opening delimiters, we also have to 1) count the number of closing delimiters, 2) Grab the difference between the 2 and then 3) append accordingly.

That's all well and good, but we're not done yet. What about mixed delimiters? Like so log[sin(2^{. Now we can finally discuss the fun part, step by step how your brain does (probably) it.

Simply put, your brain just scans the expression backwards really fast. If it sees an opening delimiter, it immediately appends the corresponding closing delimiter to the expression. Now add the above paragraph about checking the number of appearance to the mix and no matter what expression you feed in, it'll always output a perfectly matched output expression.

You can implement this whole thing in a switch statement that checks each unit expression (i.e log, sin, cos, (, {, )....) like so in Java-

// Inside the Switch statement
case "(":
    ++openingParentheses;
    if (openingParentheses > closingParentheses) {
        resultstr.append(")");
        closingParentheses++;
    }
    break;

Now you just have to put the whole switch statement in a reverse iterator loop!

Here it is in action!

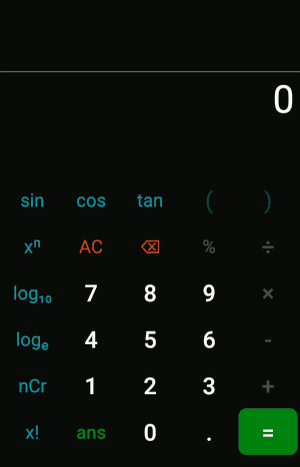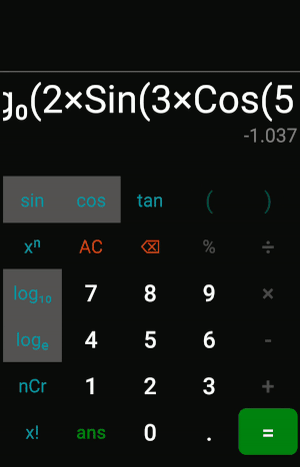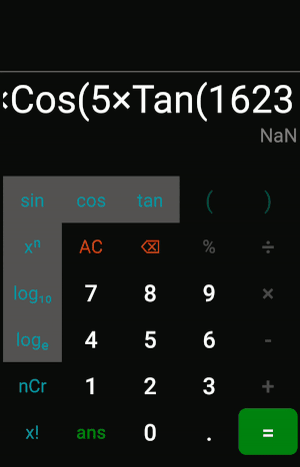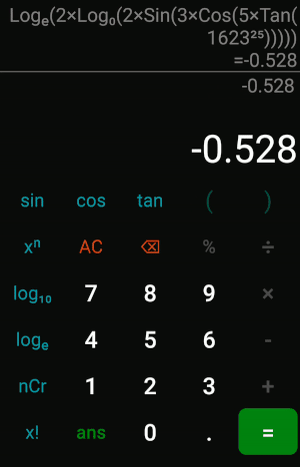
note that although the frontend shows only parentheses, the backend uses different delimiters for different functions, so it still uses the exact same algorithm

Part 2 - Function associated with given closing delimiter

Introduction

Once I was done with the auto-complete, I needed to know exactly which function is associated with which delimiter. Suppose you were given this expression log10[sin(23^{56*cos(loge[2])})] and you were told to find out which function does the second to last parenthesis belongs to. In this case, that belongs to cos. But what's the algorithm behind it?

The Algorithm

Again, I recommend opening the source code if you haven't already

Once again, we reverse iterate the expression, this time we also need a user provided index and the expression must be an array, to separate each unit expression. The expression log10[sin(23^{56*cos(loge[2])})], if turned into a String array, it'd be-

{"log10", "[", "sin", "(", "23", "^", "{", "56", "*", "cos", "(", "loge", "[", "2", "]", ")", "}", ")", "]"}        

This time, we start reverse iterating from the given index, but skip the index itself. So, the index of the second to last parenthesis in this array is 15. So we'll start reverse iterating from 14.

Now, the reverse iteration must go on until the number of appearances of opening delimiters is greater than(not equal to) the number of appearances of closing delimiters. The moment the loop stops, wallah!, you magically have the index of the corresponding function, in this case, cos.

Well, not magically, but you know what I mean.

If we wanted to implement this for parentheses ((). We'd do it like so;

while (openParentheses <= closeParentheses) {
    switch (expression[i]) {
    case ")":
        closeParentheses++;
        break;
    case "(":
        openParentheses++;
        break;
    }
    i--;
}

The resulting i is the index of the function.

Here it is in action!

notice that whenever I remove a closing delimiter using backspace, the program is able to tell which function region I just entered

Conclusion

That's it! That's how your brain does it (probably). I found it really fascinating at first and when I figured out the algorithm, it felt really nice. I figured I'd share with everyone!

Once again, if you need to use it in any of your java programs, I personally used it in Android dev stuff, you can just grab the .jar file from the repo!