Trees, oh glorious trees, they provide us shade, oxygen, and a way to optimize our collision system. Recently at Wooden H Studio we have been working on trying to implement a Quad Tree system to help optimize our mesh collisions.
What’s a Quad Tree?
A Quad Tree is a tree that uses a recursive pattern that subdivides itself into 4 other quad trees, insert a point into itself or one of its children, and query how many point are within a defined region like a rectangle or a circle, this type is mainly used for 2D applications. Additionally, quad trees have a long lost brother named Octrees, the main difference between them is rather than splitting into 4 sections it splits into 8 sections and is mainly used for 3D applications.
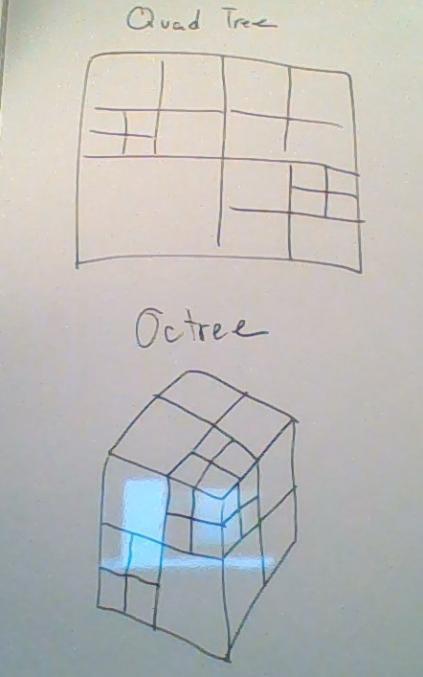
So how do you use one?
The way both of these trees work is they have a capacity for how many objects can be inside a section at each time for example we will assume our capacity is 3. As long as we stay underneath or equal to the capacity we do not need to divide our tree
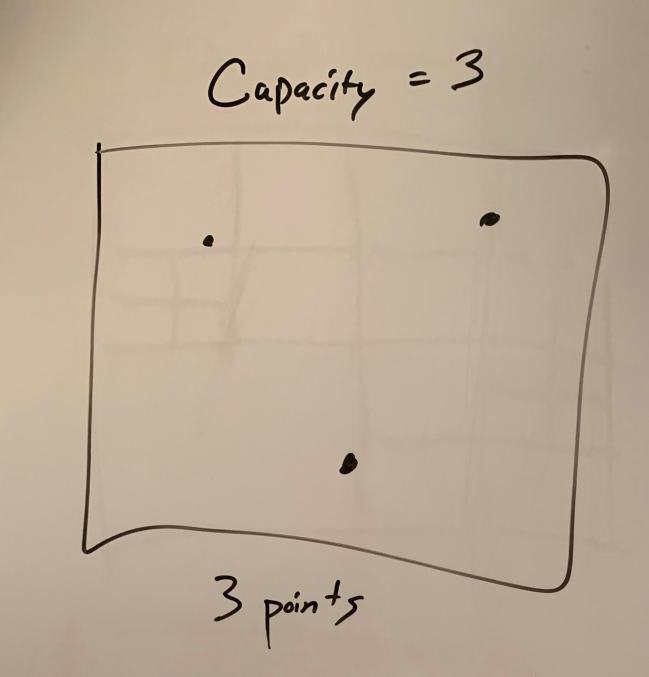
But, once we go over that capacity we need to subdivide. Regardless of where the new point is it is prefered that we split it evenly to avoid confusion.

How does this help us?
Well as I said before this will help us optimize our newest problem, mesh collisions. Now we could use an Octree for this but the problem is we have very limited memory and while this is pretty fast it does use a fair amount of memory. The other reason why we opted for the quad tree is the only thing we are using the mesh collision for is the ground. Since our ground is going to be hilly and rugged we find the centroid point of our triangle and insert it into our quad tree. Since we don’t plan on our environment moving around and changing we can pre-compute this before the game begins and call a query to reduce the amount of collision checks. With this knowledge we can reduce collision checks from 200 to possibly 5, with very little complexity or even effort.
By Gage Dietz






Top comments (0)