Regression
A regression is a statistical technique that relates a dependent variable to one or more independent (explanatory) variables. A regression model is able to show whether changes observed in the dependent variable are associated with changes in one or more of the explanatory variables.
Linear Regression
In general, the computer try to draw a graph in regression from where it can predict the result. The graph can be any one but when it is an linear equation it is called Linear Regression.
Univariate Linear Regression
Univariate linear regression focuses on determining relationship between one independent variable and one dependent variable.
Formula:
The w and b are called the parameters of the model. In machine learning parameters of the model are the variables which can be adjusted during training in order to improve the model.
Basically the model will try to find the best w and b for the model while training.
Cost Function
This is literally an "Standard Deviation" which helps the model to measure if it is efficient enough.
There are other formula of cost function. But we will be using this one.
Cost function helps us to find the difference of the predicted result and real result from the dataset. Target of the model will be reducing the cost function which will reduce the difference and gives us more accurate result.
Gradient Descent
It is an algorithm which is used to minimize any function and we will use that to minimize the cost function. At first start off with some initial guesses for w and b which generally 0. Then it will keep on changing the parameters w and b a bit every time to to reduce the cost function. Normally there might be more than one local minima but in linear regression there will be only one minima. So, for now we don't have to think about that.
Here alpha is the learning rate which is a small positive number between 0 to 1. We can consider it as how big steps we are taking to reach the minimum.
If the learning rate is too small, gradient descent will work but it will be slow.
If the learning rate is too big, it may always skip the minimum because of the big steps. So it may fail to converge and may even diverge.
#Importing modules
import numpy as np
#Function for computing cost
def compute_cost(x_train, y_train, w, b):
m = len(x_train)
cost = 0
for i in range(m):
f_wb = w * x_train[i] + b
cost += (f_wb - y_train[i]) ** 2
return cost / (2 * m)
#Function for computing gradient
def compute_gradient(x_train, y_train, w, b):
m = len(x_train)
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = w * x_train[i] + b
dj_dw += (f_wb - y_train[i]) * x_train[i]
dj_db += (f_wb - y_train[i])
return dj_dw/m, dj_db/m
#Function for gradient descent
def gradient_descent(x_train, y_train, w_init, b_init, alpha, num_iters):
w = w_init
b = b_init
for i in range(num_iters):
dj_dw, dj_db = compute_gradient(x_train, y_train, w, b)
w -= alpha * dj_dw
b -= alpha * dj_db
return w, b
#Data sets
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
#Initial w and b
w_init = 0
b_init = 0
#Some values for gradient descents
alpha = 0.01
num_iters = 100000
print(gradient_descent(x_train, y_train, w_init, b_init, alpha, num_iters))
Above is the python implementation of gradient descent for univariate linear regression where we have only 2 data in the dataset. But larger dataset are always better for training.



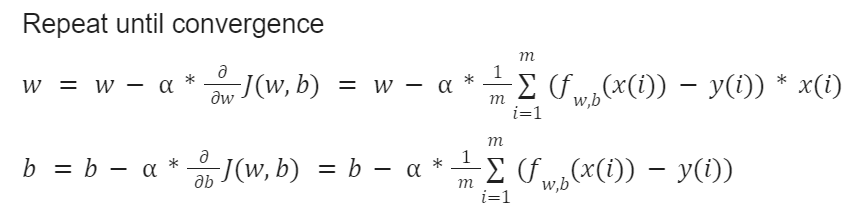

Top comments (0)