Descomplicando Machine Learning - Parte IV

Motivação

No ultimo artigo, falamos da importancia do CRISP-DM e vimos que o CRISP-DM emerge como uma estrutura proeminente, oferecendo uma abordagem sistemática e flexível para enfrentar os desafios complexos da mineração de dados. Também vimos que o CRISP-DM está subdividado em 6 parte, onde falamos das três primeiras fase e hoje vamos falar da quarta (Modelagem) e a Quinta fase (Evolutation) do CRISP-DM

Apesar que num projeto de machine learning gasta - se mas tempo na fase de preparação de dados, não é com isso que a fase da modelagem é a mais facil, pelo contrário dependendo da dimensão do projeto, modelagem é uma das fase complexa no ciclo de vida de desenvolvimento de um modelo de aprendezagem de máquina. E o nosso objectivo com este artigo de hoje é propor uma abordagem que pode servir de boilerplace na hora de fazer modelegam. Vamos á isso?

NOTA: Com o intuito de evitar que o artigo se transforme em um tutorial, iremos enfatizar apenas as partes essenciais. Para uma experiência mais completa ao seguir o artigo, não deixe de consultar o notebook do projeto.

4º Fase do CRISP-DM - Modelagem

Criar modelos em machine learning refere-se à etapa em que um modelo é desenvolvido usando algoritmos específicos e dados de trainamento para realizar tarefas específicas.

Na minha opinião, esta é a fase mais fascinante de um projeto de machine learning, pois é aqui que os elementos se entrelaçam para criar um produto utilizável pelo utilizador final. Para conduzir esta fase, vamos seguir os seguintes pontos:

1. Compreender a correlação entre a variável preditiva (o target) e as outras variáveis explicativas.
2. Preparar os dados para os algoritmos de machine learning.
3. Aplicar o dimensionamento de características (feature scaling)
4. Selecionar, treinar o modelo e avaliar o desempenho.

1. Compreender a correlação entre a variável preditiva (o target)

A correlação de dados em machine learning refere-se à medida estatística que avalia a relação entre duas variáveis. Essa relação pode ser positiva, negativa ou neutra, indicando como as variáveis mudam em relação uma à outra. A correlação é uma ferramenta crucial na fase de preparação de dados e na escolha de variáveis para construir modelos eficazes.

O coeficiente de correlação varia de –1 a 1. Quando está próximo de 1, significa que há uma forte correlação positiva; olhando no nosso exemplo, o valor médio das casas tende a subir quando a renda média aumenta. Quando o coeficiente está próximo de –1, significa que há uma forte correlação negativa como podem observar na imagem abaixo.

2. Preparar os dados para os algoritmos de machine learning

Quando abordamos a segunda fase do CRISP-DM, realizamos o carregamento do nosso conjunto de dados. Para uma compreensão mais aprofundada, essa etapa nos permitiu explorar a distribuição dos dados, enquanto lidamos com dados ausentes ao realizar imputações. Dessa forma, nosso conjunto de dados está pronto para as próximas fases.

Agora que percebemos a correlação entre os dados, uma das ações que tomaremos é a divisão dos dados, reservando 80% para o treinamento do modelo e 20% para testar o modelo treinado. Essa abordagem visa evitar tanto o subajuste (overfitting) quanto o sobreajuste (underfitting) do modelo em produção. No nosso caso, utilizamos a biblioteca scikit-learn, como mostrado no trecho de código abaixo.

from sklearn.model_selection import train_test_split

X_train, x_test, y_train, y_test = train_test_split(features, target, test_size=0.20, random_state=1)

3. Aplicar o dimensionamento de características (feature scaling)

Como observamos nas sessões anteriores, um conjunto de dados pode apresentar muitos atributos. No nosso caso, o conjunto de dados possui 9 atributos, e esses atributos podem ter magnitudes, variâncias, desvios padrão e médias diferentes. Por exemplo, a população pode estar na casa dos milhares, enquanto o preço pode estar na faixa de dois dígitos.

A discrepância nas escalas ou magnitudes dos atributos pode impactar o modelo. Por exemplo, variáveis com valores mais altos podem predominar sobre aquelas com valores menores em modelos lineares, como é o nosso caso. É ali onde entra a importancia do dimensionamento de características (feature scaling). Entretanto existem três abordagens comuns para o feature scaling:

• Padronização (Standardization): Essa técnica ajusta os valores para ter uma média zero e um desvio padrão de um.

• Normalização Min/Max (Min/Max Scaling): Redimensiona os valores para um intervalo específico, comumente entre 0 e 1.

• Normalização pela Média (Mean Normalization): Ajusta os valores para ter uma média zero.

Considerando que já temos os dados separados em um conjunto de treino e outro de teste para evitar overfitting ou underfitting, optaremos pela primeira técnica: aplicar dimensionamento de características (feature scaling). A aplicação dessa técnica é bastante simples. Basta instanciar a classe e, em seguida, chamar o método fit_transform, que realizará o feature scaling automaticamente para nós, como demonstrado no trecho de código abaixo.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
x_test = scaler.transform(x_test)

4. Selecionar, treinar o modelo e avaliar o desempenho

Finalmente! Nós definimos o problema, carregamos os dados e os exploromos, separamos um conjunto de treinamento e um conjunto de teste, aplicamos as devidas transformação agora estamos prontos para treinar o nosso modelo.

Antes de escolher um possivel algorimo, é importante saber o tipo de problema que estamos a resolver, pois este passo, vai indicar qual o algoritmo selecionar. No caso do aprendizado supervisionado temos dois tipo de problemas.

• Regressão linear: A regressão linear é um método estatístico que busca estabelecer uma relação linear entre uma variável dependente (alvo) e uma ou mais variáveis independentes (características). O objetivo é criar um modelo que represente a relação linear entre essas variáveis, permitindo fazer previsões ou inferências sobre a variável dependente com base nas variáveis independentes,por exemple prever o preço de imóveis

• Regressão logística: A regressão logística é um método estatístico utilizado para modelar a probabilidade de um evento ocorrer como uma função das variáveis independentes. Ela é particularmente adequada para problemas de classificação binária, onde o resultado desejado pode ser categorizado em duas classes, como sim OU não, positivo OU negativo, ou 1 OU 0, True OU False. por exemplo prever ser o paciente tem ou não covid-19

Uma vez que o problema que estamos modelando se enquadra na primeira categoria, vamos escolher entre uma série de algoritmos para treinar nosso modelo. Aquele que apresentar a melhor acurácia será selecionado para produção. Abaixo, vou listar os algoritmos selecionados:

• Linear Regression
• Decision Tree Regressor
• Random Forest Regression
• Support Vector Regression (SVR)

Para treinar nosso modelo, basta escrever o código abaixo, lembrando que vamos repetir até encontrarmos o melhor modelo.

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)

y_pred = lin_reg.predict(x_test)

# Vamos selecionar um registo aleatório no conjunto de dados para testar
dado_entrada = scaler.transform(features.values[5].reshape(1, -1))
previsao = lin_reg.predict(dado_entrada)
previsao

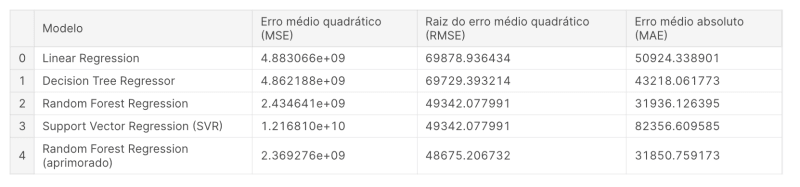
Agora que treinamos e testamos vários modelos, é hora de escolher o melhor para colocarmos em produção. Antes de escolhermos o melhor modelo, realizamos alguns testes que nos levaram ao resultado conforme mostrado na imagem abaixo.

NOTA: Escolher o melhor modelo depende do objectivo, por exemplo:

Baixo MSE/MAE: Se o seu principal objetivo é realizar previsões precisas e minimizar erros, você pode preferir o modelo com o menor MSE ou MAE

Eficiência Computacional: Árvores de decisão geralmente são computacionalmente menos dispendiosas do que florestas aleatórias. Se houver restrições de tempo de computação, uma árvore de decisão pode ser uma opção mais rápida.

Interpretabilidade: Regressão Linear e Árvores de Decisão geralmente são mais interpretáveis do que Florestas Aleatórias. Se a interpretabilidade for crucial, você pode preferir esses modelos.

Trade-offs: A Floresta Aleatória aprimorada tem um MSE ligeiramente menor que a primeira instância, mas possui um RMSE maior. Considere os trade-offs entre diferentes métricas de erro.

Generalização: Certifique-se de que o modelo escolhido generalize bem para dados não vistos. Você pode querer usar técnicas como validação cruzada para avaliar o desempenho de generalização.

5ª Fase do CRISP-DM - Refinar o modelo e escolher a melhor abordagem possível.

Após o treinamento inicial, é possível que o modelo não atinja seu máximo desempenho. A etapa de refinamento, permite ajustar hiperparâmetros, modificar arquiteturas de rede ou fazer pequenas modificações no modelo para otimizar seu desempenho. Para esse demostração usamos o algoritmo Grid Search, para retreinar o algoritmo Random Forest Regression como mostro no trecho de código abaixo:

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV

param_grid = [
    {'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]}, # Tente 12 (3×4) combinações de hiperparâmetros
    {'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},# então tente 6 (2×3) combinações com o bootstrap definido como False
]

forest_reg = RandomForestRegressor(random_state=42)

# treine em 5 dobras, totalizando (12+6)*5=90 rodadas de treinamento
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
                        scoring='neg_mean_squared_error',
                        return_train_score=True)
grid_search.fit(X_train, y_train)

grid_search.best_params_

Após executar este trecho de código, obtemos os melhores parâmetros para retrainar nosso modelo e verificar se isso resulta em um desempenho aprimorado. Para mais detalhes, não deixe de consultar o notebook do projecto

Agora que identificamos os parâmetros ideais, resta-nos retrainar nosso modelo

forest_reg = RandomForestRegressor(max_features=6, n_estimators=30, random_state=42)
forest_reg.fit(X_train, y_train)

y_pred = forest_reg.predict(x_test)

Escolher o modelo para por em produção

No nosso caso, optaremos pelo modelo Support Vector Regression Machine, e a métrica que nos levou a essa escolha foi o baixo MSE. A alternativa seria o Random Forest Regression (aprimorado); no entanto, este modelo demanda considerável poder computacional em comparação com a opção escolhida

Conclusão

Hoje, abordamos as etapas 4 e 5 do CRISP-DM. Na prática, exploramos como identificar a correlação entre a variável dependente e as variáveis independentes, aprendemos a preparar os dados para os algoritmos de machine learning, aplicamos o dimensionamento de características (feature scaling), discutimos como selecionar, treinar o modelo e avaliar seu desempenho, e, por fim, refinamos o modelo para escolher a melhor abordagem possível.

No próximo artigo, colocaremos nosso modelo em produção, utilizando ferramentas como Docker para aproveitar o conceito de infraestrutura imutável, Flask para o backend, React JS para o frontend. Estou empolgado para levar nosso modelo à produção. E você, está animado? Sendo assim, nos vemos no próximo sábado. Cuide-se!