Part 12 of this series in data structures.
Last week I learned that Dev supports the collection of posts in a series, which means that I can avoid constantly pointing back to the beginning of this series at the top of every post!
So far we've seen how to build a simple AVL tree that is stored in a buffer. In this post, we will be looking at a new property for data structures: Persistence. "Persistence" is sometimes used as a label for storing data in some external media, as we have already been doing, but I will be using a different definition here. For data to be "persistent" we will not allow it to change after it reaches the initial shape that we want. Data that has been stored will instead be called "Durable".
Functional Structures
Persistent data is a concept that is very common in Functional Programming (FP). This is a programming paradigm that can provide many benefits, even when other elements of a system are not using it. It reduces complexity by managing state, which can result in more reliable systems. These are ideas that we will be applying here.
One element of FP is that functions must be "pure", meaning that there must be no side-effects on the data passed to a function. Whatever the data looked like before the function was called is what it should look like after. This means that data structures cannot be modified. The practical outcome of this is that any operation to change data will result in a new structure rather than a modification to the old structure.
To consider this, let's look at adding a new number to a list of numbers. A naïve implementation might simply copy the original data structure, add the new number to the copy, and return that structure. While this will work, it also has a significant cost in speed and memory consumption.
A better approach is to use structural sharing, in which a new object is created that refers to data in the original object. We have already seen this when we created linked lists in Part 2. Every time we added a new number to the head of the list, the previous list was left untouched. We kept updating the head of the list, but any previous head of the list was still valid to use and continued to reference the same list, even if many items were added later.
We also call data structures that are never modified "Immutable".
Functional Trees
Let's consider how we might modify a more complex immutable structure like a tree.
The following balanced tree contains a series of numbers stored in order. In this case, we may want to change the number 20 to 21. This does not require new data to be inserted or removed, nor does anything need to be reordered.

The first step is to copy the node to be modified. This copies both the children of the node as well as the contents of the node. The references to the child nodes in the original structure are shown here with dashed lines.
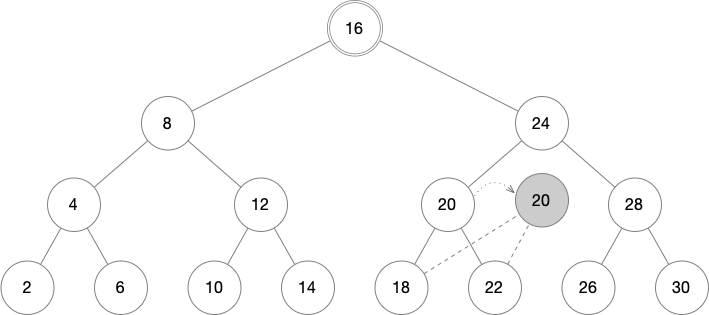
From this new node, all the parent nodes going right back to the root must also be copied. One child of each parent will continue to refer back to the original tree (shown as a dashed line), while the other child will be a newly copied node. In this way, an entire branch of the tree is copied.

With the new copy, the contents of the node can be changed with no consequence to the original tree. We now have 2 separate tree roots, labeled "A" and "B".

If we follow the tree starting at root A, we will see the original structure completely unchanged. Following the tree from root B will look almost the same, but will instead contain the number 21 rather than 20. Note that only 3 shaded nodes were copied out of the 15 nodes in the original tree. The rest of the structure is shared.
Modifying Persistent AVL
Updating a single node in-place is an unusual operation. Instead, the primary operations in trees are additions and removals.
Removal
So far, we have not discussed removing a node from an AVL Tree. There are a couple of reasons for this:
- For many applications, accumulating and indexing data is the primary task. Updating existing data in these systems is either less common or not required at all.
- While the best case complexity of deleting an AVL node is O(1), and the average is very close to this, the worst case is O(log(n)). This worst-case scenario involves rotations going all the way up to the root and misses the benefits that choosing an AVL Tree would provide. Rather than handling the expense of tree modifications, many applications avoid removing AVL nodes, and simply mark them as unused. We will be taking this approach, though it can be revisited depending on how the tree is to be used.
Whether deletions in the tree are handled via marking-as-unused or removal-and-rebalance, the principle of copying branches is identical to other updates.
Insertion
We have already looked at the mechanics of adding nodes and also updating in-place. Depending on the deletion strategy, there may also be the possibility of re-using a cleared node in the tree. This is more expensive, as it requires searching the branch to the left for the largest value, and searching the branch to the right for the smallest value to determine if a blank node can be reused for an insertion. If space is tight then this may be desirable, but generally, this is ignored, and these nodes will be removed later during system upkeep (a topic for later on).
In general, node insertion into an AVL Tree will always be at a leaf position. This will involve copying the branch in a line all the way to the root. Rebalancing always involves nodes that are directly in this pathway, so there are no extra node copies needed when this happens.
Redundancy
So far, we have only considered persistent structures through a single update operation. However, if this scheme were adopted consistently, then every single insertion would create a new root of the tree. A tree with 100 nodes would leave a trail of 99 trees behind it! This will both slow down the entire process, and expand in storage with the square of the input. This is clearly not scalable.
However, it is rare that data will need to be inserted into an index one single item at a time. Indexing is typically done in bulk, or on groups of objects. We only want to create a single new root for the tree whenever a group of data is being inserted. We can accomplish this with a "transaction".
Transactions
A "transaction" in a database allows a group of operations to be treated as a single operation. Either everything succeeds, or nothing does.
We can use this concept to create a single new root for the tree, based on a series of operations. During the transaction, all new parts of the tree can be modified as we have before, while old parts of the tree must be copied before they can be modified. Once the transaction is complete, the new root of the tree is fixed, and no more changes to that tree are possible. This is called committing the transaction. Alternatively, if something were to go wrong, all the new nodes can be abandoned and the previous root of the tree maintained. This is a transaction rollback. A useful aspect of the rollback is that all new nodes are assigned at the end of the buffer, meaning that the pointer for allocating the next node need only be wound back to where it was at the beginning of the transaction to reuse that part of the buffer in future transactions.
To implement transactions like this, we can assign each transaction a unique ID, and mark each node with the transaction it was created in. These IDs need only be an incrementing number.
When a node is to be updated, the transaction ID of the node can be compared to the current transaction, and if it matches then the node can be modified immediately. Otherwise, a copy of the node must be made, and it is that copy that will be updated.
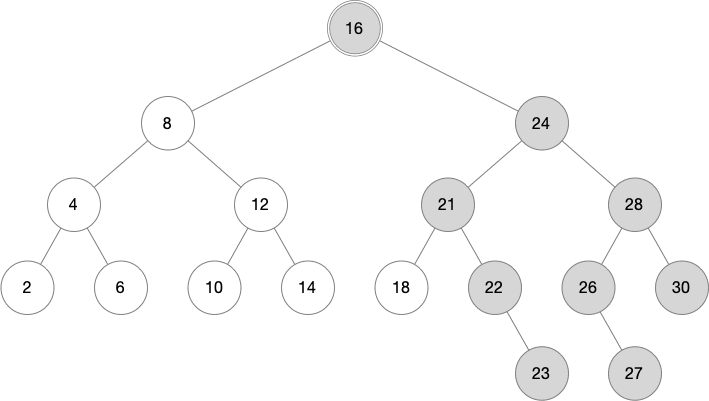
Let's see how this works with a transaction that inserts the numbers 23 and 27 into the tree above.
The first step inserts the node containing 23. This creates copies of the nodes going back to the root, containing 22, 21, 24, and 16.

The second step needs to insert under the node containing 26. This goes back towards the root, creating copies of the nodes 26 and 28. However, when the process gets to node 24 it will see that the node was created in the current transaction and can stop at this point.

The following image shows the latest version of the tree. Note that the shaded nodes were created in the latest transaction, while the white nodes were from an earlier state. The previous tree has not been lost and can still be read, but accessing that data will start at the previous root, which is not shown here.
Javascript
To see this in action, let's update the existing Javascript.
The first thing to update is the Node class. We need to add a transactionId value, as well as a new copyOnWrite method. Because it's good practice, access to the balance value will move into a setter and getter.
class Node {
constructor(transactionId, value) {
this.transactionId = transactionId;
this.value = value;
this.balance = 0;
this.children = [undefined, undefined];
}
updateChild(side, child) {
let index = side == LEFT ? 0 : 1;
this.children[index] = child;
return this;
}
setChild(side, child) {
this.updateChild(side, child);
this.balance = (this.balance === undefined) ? side : this.balance + side;
return this;
}
getChild(side) {
return this.children[side == LEFT ? 0 : 1];
}
getBalance() {
return this.balance;
}
setBalance(balance) {
this.balance = balance;
return this;
}
copyOnWrite(transactionId) {
if (this.transactionId === transactionId) {
return this;
} else {
let node = new Node(transactionId);
node.value = this.value;
node.balance = this.balance;
node.children = this.children.slice();
return node;
}
}
}
We can see here that copyOnWrite method checks if the node matches the provided transaction ID, and if so then the original node is returned. Otherwise, a new copy of the node is created, using the new transaction ID. Note that the references to the child nodes are also copied over with the call to Array.slice().
The Tree class will now need to hold information about the current transaction, along with the transaction ID counter. We want to be able to clone a tree to represent new versions, so we'll remove the constructor that takes an initial value (it was redundant, as the initial value can be added with add), and replace it with a cloning constructor:
class Tree {
constructor(other = null) {
if (other === null) {
this.root = null;
this.nextTransaction = 0;
} else {
this.root = other.root;
this.nextTransaction = other.nextTransaction;
}
this.transactionRoot = null;
this.transactionId = null;
}
// continues...
If no other tree is provided, everything is initialized to null, but otherwise, the root node reference and the current transaction counter are copied.
Now that these values are available, we can manage transactions:
// class Tree
startTx() {
this.transactionId = this.nextTransaction++;
this.transactionRoot = this.root;
return this;
}
commitTx() {
var nextTree = new Tree(this);
this.transactionId = null;
nextTree.root = this.transactionRoot;
this.transactionRoot = null;
return nextTree;
}
rollbackTx() {
this.transactionId = null;
this.transactionRoot = null;
return this;
}
Starting a transaction increments the ID counter, sets the current transactionId, and sets the transactionRoot to point to the current root of the tree. Rolling back the transaction just means unsetting these values.
The commitTx() method is where the real work occurs. A new tree is cloned from the current tree, and the root of the new tree is set to the root that was being updated in the running transaction. It is this new tree that gets returned. Consequently, committing a transaction will reset the current tree to the state it was in before the transaction started, but an entirely new tree structure is returned containing all the new data. This gives us access to the data both before and after the transaction.
Adding a value now needs to ensure that a transaction is running. The new node created is given the current transactionId, and the transactionRoot is modified instead of the tree root. Note that the only place where the root of the tree is set is when creating a new tree in commitTx. Once a tree is created, the root will never change.
add(value) {
if (this.transactionId == null) {
throw "Update occurred outside of a transaction";
}
let node = new Node(this.transactionId, value);
if (this.transactionRoot === null) {
this.transactionRoot = node;
} else {
this.transactionRoot = this.insertNode(this.transactionRoot, node);
}
return this;
}
Finally, the insertNode function is updated to take transactions into account. So that the current transactionId is available, we will move this function into the Tree class. We will also update the access to balance to use the new getter/setter methods:
insertNode(node, newNode) {
let side = (newNode.value < node.value) ? LEFT : RIGHT;
node = node.copyOnWrite(this.transactionId);
if (node.getChild(side) === undefined) {
return node.setChild(side, newNode);
} else {
let childBalance = node.getChild(side).getBalance();
node.updateChild(side, this.insertNode(node.getChild(side), newNode));
// Did the child balance change from 0? Then it's deeper
if (childBalance == 0 && node.getChild(side).getBalance() != 0) {
node.setBalance(node.getBalance() + side);
}
}
if (Math.abs(node.getBalance()) == 2) {
return rebalance(node);
}
return node;
}
The only difference from the previous version of this function is the call to node.copyOnWrite(), which will create a new copy of the node if it is not already in the current transaction. As a result, the reference to the provided node will not be modified if it came from the original tree.
This method is a part of the Tree class and not the Node class for a couple of reasons. The first is because the Tree class contains the transactionId value for the current transaction. The second reason is that this method may return a different Node instance to the one that it starts with. It is possible to put the method on the Node class, passing the transaction ID as a parameter, and working with this as the node instead of an explicit argument, but this does not align well with the idea of a Node method operating on the state of that node.
Testing
With these changes in place, we can see the new behaviour by adding the data to the tree in stages. The following comes from a node.js session, where each line typed by the user begins with > or .... These are always followed by the result printed pressing [Enter].
> let digits =
... [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 4, 6, 2, 6, 4, 3, 3, 8, 3, 2, 7, 9, 5, 0,
... 2, 8, 8, 4, 1, 9, 7, 1, 6, 9, 3, 9, 9, 3, 7, 5, 1, 0, 5, 8, 2, 0, 9, 7, 4, 9, 4, 4, 5, 9, 2, 3, 0];
undefined
> var pi = new Tree();
undefined
> pi.startTx();
Tree {
root: null,
nextTransaction: 1,
transactionId: 0,
transactionRoot: null
}
This created the digits array to insert, and set the tree to start accepting data in a transaction. We can see the initialized values of the tree, including the current transactionId of 0.
Now we can add the first half of our 66 digits and commit:
> digits.slice(0, 33).forEach(d => pi.add(d));
undefined
> var halfPi = pi.commitTx();
undefined
If we look at pi we can see that it has gone back to being an empty tree. The new halfPi value contains all the data so far. We will see that when we start a new transaction:
> pi
Tree {
root: null,
nextTransaction: 1,
transactionId: null,
transactionRoot: null
}
> halfPi.startTx();
Tree {
root: Node {
transactionId: 0,
value: 5,
balance: 0,
children: [ [Node], [Node] ]
},
nextTransaction: 2,
transactionId: 1,
transactionRoot: Node {
transactionId: 0,
value: 5,
balance: 0,
children: [ [Node], [Node] ]
}
}
> digits.slice(33).forEach(d => halfPi.add(d));
undefined
> var fullPi = halfPi.commitTx();
undefined
Let's try looking at the three different stages:
> toArray(pi)
[]
> toArray(halfPi)
[
0, 1, 1, 2, 2, 2, 2, 3, 3,
3, 3, 3, 3, 3, 4, 4, 4, 5,
5, 5, 5, 6, 6, 6, 7, 7, 8,
8, 8, 9, 9, 9, 9
]
> toArray(fullPi)
[
0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2,
2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5,
5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7,
7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9,
9, 9, 9, 9, 9, 9
]
We can see that each version of the tree contains only the data that was committed to it, and was not modified by later actions. We can check this for correctness by comparing to the sorted digits:
> toArray(halfPi).join(',') === digits.slice(0, 33).sort().join(',');
true
> toArray(fullPi).join(',') === digits.sort().join(',');
true
The full code for this can be found on Github.
Recap
This post showed how trees can be updated to create persistent data structures. These are data structures that can be updated in a single transaction to a new state, without modifying existing data. Doing this in memory can be simpler than we showed here, but the approach we are taking is consistent with the buffer-backed trees we developed in Java in the previous post.
In the next post, we will update our AVL tree to be both durable and persistent, and add some new features in the process.


Top comments (0)