Jared Nielsen

Posted on Jan 24, 2020 • Edited on Feb 1, 2020 • Originally published at jarednielsen.com

What is Big O Notation?

#career #javascript #algorithms #computerscience

Is there a computer science topic more terrifying than Big O notation? Don’t let the name scare you, Big O notation is not a big deal. It’s very easy to understand and you don’t need to be a math whiz to do so. In this tutorial, you'll learn the fundamentals of Big O notation, beginning with constant and linear time complexity with examples in JavaScript.

Note: Amazon links are affiliate.

This is the first in a series on Big O notation. If you want to stay in the loop, sign up for my weekly newsletter, The Solution.

What Problem(s) Does Big O Notation Solve?

Big O notation helps us answer the question, “Will it scale?”
Big O notation equips us with a shared language for discussing performance with other developers (and mathematicians!).

What is Big O Notation?

Big O is a notation for measuring the performance of an algorithm. Big O notation mathematically describes the complexity of an algorithm in terms of time and space. We don’t measure the speed of an algorithm in seconds (or minutes!). We measure the rate of growth of an algorithm in the number of operations it takes to complete.

The O is short for “Order of magnitude”. So, if we’re discussing an algorithm with O(n), we say its order of magnitude, or rate of growth, is n, or linear complexity.

You will probably read or hear Big O referred to as asymptotic runtime, or asymptotic computational complexity. This is a fancy way of describing the limits of a function. There is a branch of mathematics, order theory, devoted to this topic. For our intents and purposes, order:

… provides a formal framework for describing statements such as "this is less than that" or "this precedes that".

We use order to evaluate the complexity of our algorithms.

Math O’Clock 🧮 🕐

You don’t need to be a math whiz to grok Big O, but there are a few basic concepts we need to cover to set you up for success.

If you recall from algebra, you worked with functions such as f(x) and g(x), and even did things like f(g(x)), where f() and g() were equations and x was a numerical value (or another equation!) passed to the functions.

When we’re programming, we give our “equations” descriptive names (at least I hope you are), such as isAuthenticated and calcuateMedian, but we could also name them f and g (please don’t).

Let’s say f(x) is equal to 3x² + 12x - 6.

We could say that the order of magnitude, or rate of growth, of f(x) is O(n²⁾. We’ll see why later.

It’s more common to simply say “f(x) is order of n^2”, or “f(x) is Big O of n^2”.

Math time over.

For now. 😀

How Does Big O Notation Work?

Big O notation measures the worst-case runtime.

Why?

Because we don’t know what we don’t know.

If we’re writing a search algorithm, we won’t always know the query ahead of time. If we’re writing a sorting algorithm, we won’t always know the dataset ahead of time. What if the query is the very last element or what if the dataset is a real mess. We want to know just how poorly our algorithm will perform.

The worst-case scenario is also known as the “upper bound”. Limits again!

You’re going to encounter a lot of tables like this:

O	Run time
O(1)	constant	fast
O(log n)	logarithmic
O(n)	linear
O(n * log n)	log linear
O(n²⁾	quadratic
O(n³⁾	cubic
O(2ⁿ⁾	exponential
O(n!)	factorial	slow

This lists common runtimes from fastest to slowest.

We’ll refer to this a lot as we proceed.

Before we get into any code, let’s get hands-on to get a feel (pun intended) for Big O. We’ll use an example from Grokking Algorithms.

Let's say I give you a square piece of paper and ask you to divide it into sixteen squares. How would you approach this problem?

You could take the brute force approach and draw sixteen individual squares. If you take this approach, how many steps, or computations, will you perform?

Sixteen.

Is there an approach that requires fewer steps? Of course!

Fold the paper in half. Then in half again. Four squares!

Now fold it in half two more times.

When you unfold it, the paper will be divided into sixteen squares.

How many steps, or computations, were required?

Four.

In Big O notation, our first approach, brute force, is O(n), or linear time. Creating sixteen squares requires sixteen operations. But our second, refactored and optimized, approach is O(log n), or logarithmic time (the inverse of exponentiation). Creating sixteen squares requires only four steps.

We’ll look at O(log n) later. Let’s begin with O(1), which will help us understand O(n).

O(1): Constant Time Complexity

Say you’re working with an API that returns a users full name in an array, like so:

[“Jared”, “Nielsen”];

Your task is to get the users first name. Easy, in JavaScript:

const getFirstName = data => {
    return data[0];
}

No matter how many times you run your ‘algorithm’, it only needs to perform one operation to return the desired value. That’s O(1), or constant time.

Here’s another JavaScript example:

const isEven = num => num % 2 === 0;

Our algorithm checks whether or not a number is even or odd and will return true or false accordingly. It only needs to perform one operation. Again, O(1).

What is Big O Notation?

Big O notation is not a big deal. It’s very easy to understand and you don’t need to be a math whiz to do so. In this tutorial, you learned the fundamentals of Big O notation, as well as constant and linear time complexity with examples in JavaScript.

Stay tuned for part two of this series on Big O notation where we'll look at O(n), or linear time complexity. If you want to stay in the loop, sign up for my weekly newsletter, The Solution.

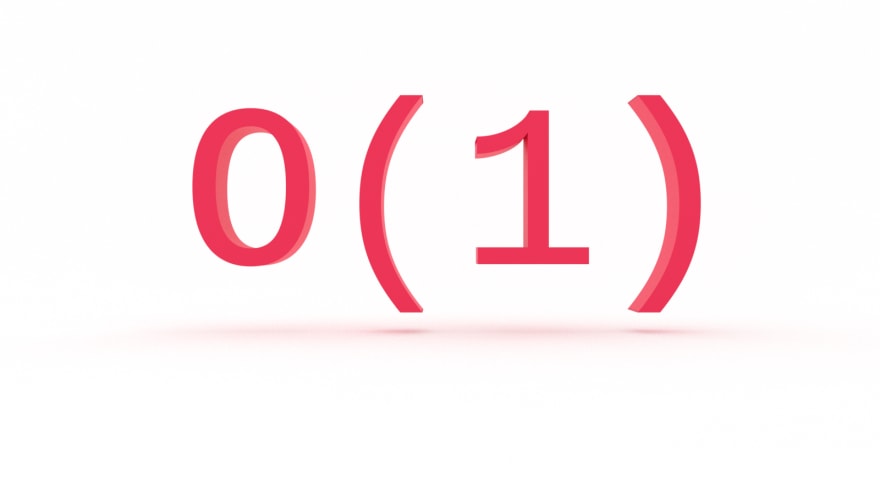
Top comments (24)

Aleksandr Hovhannisyan • Jan 24 '20 • Edited

const alertColor = state => {
   if (state === 'danger') {
       return 'crimson';
   } else if (state === 'warning') {
       return 'orange';
   } else if (state === 'success') {
       return 'chartreuse';
   } else {
       return 'cornflowerblue';
   };
}

What is our best-case scenario for this algorithm? If state is equal to danger, we will only perform one operation and return. That would be O(1). What if state is not equal to danger? Then we perform multiple operations and the order of alertColor() is n.

This is wrong. To claim that alertColor is O(n) in the worst case suggests that the function performance scales linearly with the size of the input—it doesn't. That's what Big-O (and other) notations really measure: How a routine's performance scales with the size of the input.

Even though you have potentially n or k or whatever number of if/else if statements in that function, that does not mean that the routine performs at O(n) complexity in the worst case.

Why? Because n is not variable—it remains constant regardless of how complex the input becomes. And hence the routine is really O(1).

Keep in mind that Big-O notation is about asymptotic performance. So if n, the number of if statements, is 5 or 1,000, it doesn't matter—that's a constant function of the input:

O(input size) = 1,000 = O(1)

One final remark, for the beginners out there:

Big O notation is not a big deal. It’s very easy to understand and you don’t need to be a math whiz to do so.

As much as I'd like this to be true, it's not. The examples you gave in this post are trivial. You don't need to be a math "whiz", but knowledge of math (specifically summations and the rules for simplifying them) is pretty important for more complex problems. Trying to present the examples in this post as anything but trivial is disingenuous.

aRtoo • Jan 24 '20

question though. What if there's a nested ifs then It would be an O(n) isn't it? since it will try to evaluate the nested ifs?

Aleksandr Hovhannisyan • Jan 24 '20 • Edited

No, the only thing that matters is what you're doing inside the if statement that evaluates to true. If it's an O(n) routine, like calling a method that loops over an array input, then yes:

if (true) {
 doBigOofNRoutine();
}

But in this case, simply nesting if statements doesn't change the overall complexity. That just adds +1 to the number of atomic operations that have to be done in the worst case: you perform n atomic checks before you get to the else statement, then one more for the nested if inside, and +1 (presumably) for whatever that if is doing. I say presumably because I don't know—maybe it's doing two, three, four, or a variable number of operations.

But again, the n here is a constant, not a variable that depends on the input size. So it collapses to O(1) asymptotically. It's about limits.

aRtoo • Jan 24 '20

ohh. I really thought its O(n) because it will try to evaluate every ifs.

Unless for switch statement, compiler will try its best to optimized and it will be much faster lookup. Im talking about c++ btw. thanks

Aleksandr Hovhannisyan • Jan 24 '20 • Edited

Nope. A good way to understand why it's O(1) is to consider a function that accepts an array of length n and does the same thing as in this example:

const doSomething = arrayOfLengthN => {
   if (something) {
       return 'crimson';
   } else if (somethingElse) {
       return 'orange';
   } else if (yetSomethingElse) {
       return 'chartreuse';
   } else {
       return 'cornflowerblue';
   };
}

Let's use k to denote the number of if/else if/else conditions we evaluate, to avoid confusing this with n, the length of the array we pass in to the function.

If we pass in an array of length 50, the worst-case complexity is O(k) = O(1), because all we're doing is evaluating k conditionals and returning k strings. If we pass in an array of length 1,000,000, we still only evaluate k conditionals, each one performing the same atomic operation as when we passed in a smaller array. So it's still O(k) = O(1).

Now, suppose instead that one of these conditionals runs a loop over the array:

const doSomething = arrayOfLengthN => {
   if (something) {
       return 'crimson';
   } else if (somethingElse) {
       return 'orange';
   } else if (yetSomethingElse) {
       arrayOfLengthN.forEach(element => console.log(element)); // here
   } else {
       return 'cornflowerblue';
   };
}

The worst case is if we reach yetSomethingElse and it's true. In that case, the worst-case complexity of the overall function, doSomething, is O(n). Unlike k, notice that n is a variable and not a constant/fixed value—it depends on the size of the input.

I hope that clears things up.

Aleksandr Hovhannisyan • Jan 24 '20

It's also good to keep in mind that there is nothing special about n.

Saying an algorithm is O(n) without defining n is a little misleading, even though it is traditionally taken to be the size of the input.

In the example with all the if statements, if we define n to be the number of if statements, then the algorithm is in fact O(n). But n is just a constant, so it's really O(1).

aRtoo • Jan 24 '20

yea i got you now. on your example since arrayOfLengthN is just being compared then run time would always be constant unless n is being run by or evaluated by other method such as forEach. In other words compare instruction is O(1) regardless of how many are being chained.

aRtoo • Jan 24 '20

In the example with all the if statements, if we define n to be > the number of if statements, then the algorithm is in fact O(n). > But n is just a constant, so it's really O(1).

Im guessing the author is talking about n as number of ifs thats how I was understanding it. Thats why he had to create a hash for a constant look up.

Aleksandr Hovhannisyan • Jan 24 '20

In other words compare instruction is O(1) regardless of how many are being chained.

Exactly, unless they're doing something with the input data that would scale with the input size.

aRtoo • Jan 24 '20

gotcha. much love sir. thanks.

Paceaux • Jan 24 '20

I've probably read a dozen article on Big-O notation and this is the first one I was able to get through by reading it exactly once.

Jared's examples are intentionally trivial because his intended audience is beginners. Content of your comment makes it pretty clear that you are not the target audience.

Coming into an introductory article and saying, "the examples ... are trivial", as though it were a bad thing, is not helpful; in fact it's hurtful. Why should beginners be given complex examples first? What possible gain is there?

Jared Nielsen • Jan 24 '20

Thanks for catching my error, Aleksandr. That was a holdover from an earlier draft. The perils of being your own editor. But it generated a great discussion! Update forthcoming.

Rodion Gorkovenko • Jan 24 '20 • Edited

Hi Jared! Honestly, I'm not sure JavaScript is good choice to discuss O-notation and time complexity.

Arrays in JavaScript are not just plain arrays. Depending on implementation they have hastable inside and, probably, not only this. I do believe access is still O(1) "amortized", but it may be funny to try inventing test-case for which it doesn't hold.

Theofanis Despoudis • Jan 24 '20

True. If you assign a different unit-cost for each operation based on the lower implementation details you might get surprised of how different complexities can you get. If we assume a simple model though it's easier to comprehend.

Rob Conery • Jan 25 '20 • Edited

Hi Rodion - I think there's some confusion and I'd like to see if I can help clear it up :).

Arrays in JavaScript are not just plain arrays

If you mean that there aren't pointers in memory - yes! True. They can also act like stacks/queues depending on how you use them. The thing is: whether they're an array or not is beside the point when you're discussing Big-O. The big thing is: are they iterable? And indeed they are. That makes their use in these examples ideal

Arrays might be collections of objects (hash tables, as you suggest) but that doesn't change the nature of the array. You still need to access the array by index as Jared has done, or you need to iterate.

Access to an array is only O(1) if you know the index and it's completely independent of what's inside the array. Either way - using JS is just fine for Jared's examples. The simpler the better!

Rodion Gorkovenko • Jan 25 '20 • Edited

Hi Rob!

Access to an array is only O(1) if you know the index

I'm not sure you can find any words in specification of JS that any JS engine is required to implement them in this way :)

E.g. there probably is no guarantee that they are not implemented as RB-trees inside. Or that current implementation (say in Chrome 80) which is based on hashtable (not sure) won't change to tree in Chrome 81.

I meant just that. JS arrays are really queer and their behavior for certain operation may differ, say, between V8 engine and Rhino :)

a = []
a[5] = 8
a.pop()
console.log(a.length)

Rob Conery • Jan 25 '20

True the implementation details aren’t on the top of my head and I totally agree it’s a weird language. Wouldn’t surprise me to find out that really, under the hood, it’s a mess. Either way Big O doesn’t care mate. That stuff (Lang or framework details) is actually beside the point. An array, as a data structure, is treated as O(1) conceptually speaking as that’s where we are... in the land of concepts.

There is a concern with true measurement (I think it’s big T or something) but Big O is meant as shorthand... like and algorithmic pronoun.

I think this is just as important a point as any other and usually where people get stuck with Big O... the “what if my input is..” or “what if I’m using X which doesn’t have Y concern”. All of those are valid! But Big O is a bit more generalized in that sense.

Jared Nielsen • Jan 24 '20

Hi Rodion! Thanks for your reply and thanks for the idea for a future post. An article about array implementation in JavaScript would be both fun to write and useful for the community. As suggested by the title, this post is intended for beginners and beginners on this platform are likely using JavaScript. The examples are used to illustrate fundamental concepts. The points you are making require deeper understanding of Big O, data structures, and JavaScript itself. Gotta start somewhere! I think this post is a good place to do just that. Cheers!

Rob Conery • Jan 24 '20 • Edited

Hi Jared - nice article. I wanted to echo what others have said that your example re alertColor() is always O(1) so you may want to tweak this:

What if state is not equal to danger? Then we perform multiple operations and the order of alertColor() is n.

The reason it's O(1) is that this algorithm will always perform the same tasks no matter the input (as there is no input).

I would encourage you to update the post so people don't get confused :).

A really helpful way to think about Big-O (in my opinion) is to ponder how many loops you have that loop over your input argument. One loop will always be O(n), nested loops are O(n²⁾ and so on. No loops at all (as in your example) is always O(1).

I wrote about Big-O here: rob.conery.io/2019/03/25/wtf-is-bi... and I also wrote a big fat book about core programming concepts which is linked on my blog... didn't come here to be cheesy I promise!

Jared Nielsen • Jan 24 '20

Hi Rob! The Impostor's Handbook is fantastic! I'm entirely self-taught and it helped me fill in gaps I didn't know I had.

Thank you for kindly flagging my error. Editorial oversight. Update in the works.

Cheers!

Rob Conery • Jan 24 '20

Cheers mate - no prob at all. This is tough stuff and my goodness did I get it wrong way too many times!

AxelleDRouge • Jan 24 '20

Woah that was so well explained, while still being entertaining!
thanks, I look forward to the next part of this series

Jessica Garson • Jan 24 '20

Awesome!

Paceaux • Jan 24 '20

I've read at least a dozen articles on Big-O throughout the years. This by far is the best explanation I've seen. Thanks for writing it and I look forward to reading your future posts.

View full discussion (24 comments)

DEV Community

What is Big O Notation?

What Problem(s) Does Big O Notation Solve?

What is Big O Notation?

Math O’Clock 🧮 🕐

How Does Big O Notation Work?

O(1): Constant Time Complexity

What is Big O Notation?

Top comments (24)

Read next

The Software Engineering Manager Role

How to Build a Strong Tech Resume (Get Hired Faster)

What is JavaScript ?

Axios interceptor + React JS