FP(06): Recursive Function ฟังก์ชันเวียนเกิด, เขียนลูปไม่ได้ทำยังไง? มาเขียนฟังก์ชันเรียกตัวเองแทนกันเถอะ!

ติดตามบทความอื่นๆ ของเราได้ที่ TAMEMO.com

ตอนแรกเนื้อหาในบทนี้จะมีพูดถึงเรื่อง Tail Call Optimization ด้วย แต่พบว่าเนื้อหามันยาววววเกินไป เลยขอตัดออกไปอยู่ในบทความต่อๆ ไปแทนนะ

Recursive Function หรือ ฟังก์ชันเวียนเกิด เป็นเทคนิคการเขียนฟังก์ชันที่เรียกตัวเอง

แต่สำหรับโปรแกรมเมอร์ทั่วๆ ไปหรือนักเรียนที่เพิ่งเริ่มเรียนเขียนโปรแกรมมักจะหลีกเลี่ยงการเขียน Recursive Function กันหมดเลย

เหตุผลคือการเขียนฟังก์ชันแบบนี้มันยาก ต้องคิดอะไรเยอะแยะซับซ้อน แถมเขียนแล้วผิดง่ายอีกตั้งหาก

ในบทความนี้เราจะมาแสดงให้เห็นว่า Recursive Function นั้นไม่ได้ยากอย่างที่คิดกัน แถมมันเข้ากับความคิดของคนเรามากกว่าเขียน loop ซะอีกนะ!

ทำไม FP ต้อง Recursive ?

สำหรับการเขียนโค้ดแบบ imperative ถ้าเราต้องการจะทำอะไรซ้ำๆ เรามี 2 ทางเลือก

• Loop: ไม่ว่าจะเป็น for, while, หรือ do-while
• และ Recursive Function

แต่สำหรับโลกแห่ง FP แล้วเรามีปัญหาถ้าเราจะใช้ loop ลองดูโค้ดต่อไปนี้

for(var i=0; i<100; i++) {
    print(i)
}

นี่คือการเขียนลูปแบบมาตราฐาน คือเราต้องกำหนดค่าเริ่มต้น, เงื่อนไขว่าจะทำไปจนถึงค่าไหน, และสุดท้ายคือการอัพเดทค่าของตัวแปร

มาร์คตรงนี้ไว้เลยครับ "อัพเดทค่าของตัวแปร" ในแนวคิดแบบ FP แท้ๆ จะมีเรื่องของ Immutable หรือ แนวคิดของตัวแปรที่เปลี่ยนค่าไม่ได้ อยู่ด้วย (ยังไม่รู้ Immutable, อ่านได้ที่นี่)

ดังนั้น...

เมื่อตัวแปรเปลี่ยนแปลงไม่ได้
iterator ที่เอาไว้นับรอบของลูปก็ใช้ไม่ได้ไปด้วย
ดังนั้นเราเขียน loop ใน FP ไม่ได้นะ !!

ใช่แล้ว! ในเมื่อ FP นั้นไม่มี loop มันก็จะเหลือแต่แนวคิดแบบวนซ้ำไงล่ะ

ก่อนที่เราจะอธิบายเรื่องรีเคอซีฟฟังก์ชัน เราจะขออธิบายอีกเรื่องหนึ่งก่อน ซึ่งเป็นคอนเซ็ปมัน นั่นคือ...

Divide and Conquer

ดีไวด์ แอนด์ คองเคอร์ = แบ่งแยก และ ทำลาย เป็นเทคนิคการแก้ปัญหาแบบนึง โดยมีคอนเซ็ปคือ เมื่อเราเจอปัญหาที่ใหญ่เกินไปจนแก้ทั้งหมดในทีเดียวไม่ได้ งั้นเราก็จะแบ่งส่วนปัญหานั้นออกเป็นส่วนย่อยๆ ที่เล็กลงแล้วแกมันทีละส่วน

จริงๆ เทคนิคนี้เขาบอกว่ามาจากการสู้รบ คือถ้าเราเจอกองกำลังของศัตรูที่มีจำนวนเยอะกว่าเรามากๆ การเข้าปะทะตรงๆ กองทหารฝั่งเราน่าจะแพ้แน่นอน หนึ่งในวิธีการที่จะทำให้ฝั่งเราชนะก็คือแบ่งส่วนกองกำลังศัตรูออกเป็นหน่วยเล็กๆ แล้วค่อยๆ รุมตีหัวมันทีละกลุ่มๆ ทำแบบนี้ไปเรื่อยๆ จนกองกำลังศัตรูหมดไป

คอนเซ็ปนี้สามารถเอามาใช้ในโลกการเขียนโปรแกรมได้เช่นกัน นั่นคือเมื่อเวลาเราเจอปัญหาหนึ่ง ที่เราแก้มันไม่ได้ เราก็จะจับมันแบ่งๆๆๆ ออกเป็นส่วนย่อยๆ จนถึงจุดที่เราสามารถแก้มันได้นั่นเอง

เช่นถ้าเรามีปัญหา 1, 2, 3, 4, 5 แต่เราแก้พวกมันพร้อมๆ กันทีเดียวไม่ได้ ก็จับมันแยกออกจากกัน แล้วแก้ปัญหามันทีละตัว

เอาล่ะ กลับมาเข้าเรื่องของเรากันดีกว่า...

Recursive Function ฟังก์ชันเรียกตัวเอง

Loop และ Recursive นั้น Equivalence กัน (สมมูลกัน) คือใช้แทนกันได้ 100%

แบบที่เล่าไปในบทแรกๆ ว่าการใช้ loop นั้นเป็นของฝั่ง Imperative ซึ่งเทียบเท่าได้กับ recursive ของฝั่ง FP -> ถ้าคุณเขียนโค้ดแบบ loop ได้แสดงว่าเราเขียนโค้ดให้ในรูปแบบ recursive ได้ (และในทางกลับกันด้วยนะ)

ต่อไป จะขอยกตัวอย่างด้วยโค้ด simpleๆ คือ "เราต้องการหาผลบวกรวมของเลขทุกตัวใน array"

ซึ่งถ้าเราเขียนด้วย loop ก็จะได้โค้ดหน้าตาเบสิกๆ ที่เราเขียนกันมาเป็นสิบๆ รอบแล้ว แบบนี้

function sum(arr) {
    var sum = 0
    for(var i = 0; i < arr.length; i++) {
        sum = sum + arr[i]
    }
    return sum
}

ต่อไป เราจะมาลองเปลี่ยนโค้ดตัวนี้ให้เป็น Recursive กัน!

หา Ternimate Case ให้เจอสิ

แพทเทิร์นที่ใช้ได้กับโจทย์ Recursive แทบจะ 100% คือทันทีที่เริ่มฟังก์ชัน เราจะต้อง

• เช็กว่าปัญหาตอนนี้ของเราเล็กพอที่จะ solve หรือยัง
• ถ้าเล็กพอแล้ว ให้หาคำตอบ แล้ว return กลับไปเลย (เรียกว่า Terminate Case หรือ Base Case)
• ถ้าปัญหาใหญ่ไป ให้แตกปัญหาออก แล้ว Recursive ซะ

ลองเอามาเทียบกับโจทย์ของเรากัน

• ต้องการหาผลบวกของ array เคสไหนล่ะที่ไม่ต้องคิดอะไรเลยก็รู้คำตอบแล้ว
• นั่นคือ ถ้า array ตัวนั้นมี size=1 คือมันมีเลขอยู่ตัวเดียวยังไงล่ะ มีแค่ 1 ตัวก็ไม่เห็นต้องบวกอะไรต่อเลย นี่แหละผลบวกรวมของ array ตัวนี้แล้ว
• แต่ถ้า array มีเยอะกว่านั้น เอางี้ละกัน เราจะดึงตัวเลขตัวแรกเก็บเอาไว้ แล้วเอาตัวเลขที่เหลือไปหาผลบวก

function sum(arr) {
    // ถ้าปัญหาเล็กพอ: array มีแค่ตัวเดียว
    if (arr.length == 1) {
        return arr[0]
    } 
    // ถ้าปัญหาใหญ่ไป 
    // เก็บเลขตัวแรกไว้ แล้วนำตัวที่เหลือไปหาผลรวมมาก่อน
    else {
        return arr[0] + sum(arr.tail)
    }
}

tail คือ array ทั้งหมดที่ตัดตัวแรกทิ้งไป อ่านเพิ่มเติมได้ในบทที่แล้ว

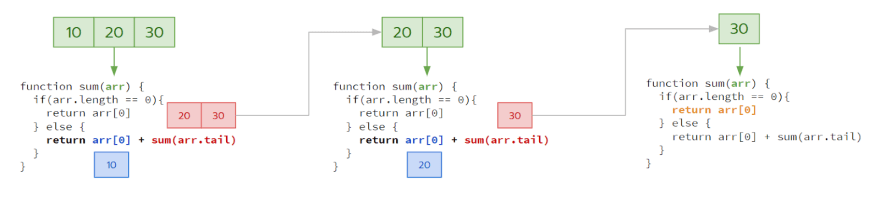
การทำงานก็จะเป็นแบบรูปข้างล่าง

สมมุติว่าเราเริ่มต้นด้วย [10, 20, 30]

• มีตัวเลขหลายจำนวน ถือว่าปัญหาใหญ่ไป ให้เก็บตัวเลขแรกเอาไว้ (นั่นคือ 10) ตัวที่เหลือ (คือ [20, 30]) ให้ส่งไปหาคำตอบต่อไป
• จนในที่สุด มันจะไปสุดเมื่อ array ของเราเหลือแค่ 1 ตัว (เข้า Terminate Case)
• ฟังก์ชันท้ายสุดก็จะทำการ return ค่าคำตอบกลับมา

• จากนั้น พวกฟังก์ชันที่รอคำตอบอยู่เป็นทอดๆ ก็จะเริ่ม return คำตอบกลับไปได้

จุดสำคัญของเรื่องนี้คือ..

• เราจะต้องมี Terminate Case ที่ครอบคลุม เพื่อหยุดการเรียกต่อๆ กันของฟังก์ชันพวกนี้
• ทุกครั้งที่เรียก Recursive ต้องมั่นใจว่าเราทำให้ Problem Size นั้นเล็กลงเรื่อยๆ ตลอด ไม่งั้นมันจะเรียกฟังก์ชันไปเรื่อยๆ ไม่มีวันสิ้นสุดนะ (เทียบได้กับเขียน infinity loop นั่นแหละ)

ถึง Recursive จะมีความหมายว่าฟังก์ชันที่เรียกใช้งานตัวเอง แต่จริงๆ มันควรจะแปลว่า "ฟังก์ชันที่เรียกใช้งานร่างก๊อปปี้ของตัวเอง" มากกว่า เพราะมันไม่ได้เรียกตัวเองตรงๆ แต่มันเรียกไปยังฟังก์ชันอื่น ที่หน้าตาเหมือนมันตั้งหาก .. อ่านแล้วงงมั้ยเนี่ย? (ฮา)

ในการเขียน Recursive Function เราต้องมีความเชื่อมั่นว่าฟังก์ชันจะทำงานได้สมบูรณ์เมื่อเขียนเสร็จแล้ว เช่นในเคสนี้ เราต้องเชื่อมั่นว่า sum() นั้นสามารถหาผลบวกได้แน่นอน (แต่ตอนนี้ยังเขียนไม่เสร็จนะ แต่เดี๋ยวจะเสร็จในอนาคต) ต้องกล้าๆ เรียกใช้ เชื่อใจในตัวเองว่าเดี๋ยวเราจำทำให้มันรันได้แน่นอน!

แต่ก็ไม่จำเป็นว่า Terminate Case จะต้องมีตัวเดียวนะ มันสามารถมีหลายตัวได้ แล้วแต่ว่าเราคิดอะไรออกบ้าง

เช่น โจทย์ข้างบน จริงๆ เรายังคิดไม่ครอบคลุมทุกกรณีนะ แบบกรณีที่อะเรย์เป็น empty array ล่ะ?

function sum(arr) {
    // Terminate Case 1
    if (arr.length == 0) {
        return 0
    }
    // Terminate Case 2
    if (arr.length == 1) {
        return arr[0]
    }

    // Divide and Conquer
    return arr[0] + sum(arr.tail)
}

เพิ่มตัวเช็กเข้าไป ว่าถ้า empty ให้ตอบ 0 กลับเลย

หรือบางคนอาจจะบอกว่า จริงๆ แล้วถ้ามีเลขอยู่ 2 ตัว (array size=2) ก็หาคำตอบได้นะ ถือว่าไม่ใหญ่มาก

function sum(arr) {
    // Terminate Case 1
    if (arr.length == 0) {
        return 0
    }
    // Terminate Case 2
    if (arr.length == 1) {
        return arr[0]
    }
    // Terminate Case 3
    if (arr.length == 2) {
        return arr[0] + arr[1]
    }

    // Divide and Conquer
    return arr[0] + sum(arr.tail)
}

จะเพิ่มไปอีกเคสแบบนี้ก็ได้นะ ไม่ถือว่าผิด! แต่ถือว่าTerminate Case Redundancy คือเคสสำหรับจบมันเยอะเกินความจำเป็นเกินไปหน่อย เพราะถ้าไม่หยุดแค่ตัวที่จำเป็น เดี๋ยวก็จะมี arr.length == 2, arr.length == 3, arr.length == 4 พวกนี้ตามมากเรื่อยๆ ไม่หมดซะที

จะแบ่งปัญหายังไงคิดไม่ออก จำไว้เลยรูปแบบมาตราฐาน

เรื่องต่อมา สำหรับคนที่คิดไม่ออกว่าจะแบ่ง Problem ออกยังไง เราถึงจะเขียน Terminate Case ได้ครอบคลุม ให้ยึดหลักการต่อไปนี้

1. Keep First / Recursive Rest: เก็บตัวแรกไว้ (และแก้ปัญหาตัวนั้น) ตัวที่เหลือนำไป recursive
2. Split Half / Recursive Both: แบ่งครึ่งเลย แล้ว recursive ทั้งสองส่วนนั้นเลย (แล้วเอาคำตอบมารวมกันทีหลังอีกที)

เช่นตัวอย่างหาผลบวกเลขใน array เราลองทำแบบแรกไปแล้ว มาลองทำแบบที่ 2 กันบ้าง

function sum(arr) {
    // Terminate Case 1
    if (arr.length == 0) {
        return 0
    }
    // Terminate Case 2
    if (arr.length == 1) {
        return arr[0]
    }

    // Divide and Conquer
    var n = arr.length
    var mid = n / 2
    return sum(arr.subarray(0, mid)) + sum(arr.subarray(mid, n))
}

ในเคสนี้ คือเราแบ่ง array ออกเป็น 2 ส่วนเลย แล้วให้แต่ละตัวไปหาผลรวมมา แล้วสุดท้ายเอามาบวกกันอีกทีนึง

ทิ้งท้าย

เรื่องของ Recursive Function นั้นจริงๆ มีแนวคิดแบบเดียวกับการเขียน loop เลย (อย่างที่บอกไปข้างต้นว่ามัน Equivalence กัน) แค่ในการเขียนโปรแกรม เรายังไม่ชินกับมันเท่านั้นเอง

โดยเฉพาะสำหรับมนุษย์ การคิดแบบ Recursive เป็นอะไรที่คิดได้อย่างเป็นธรรมดาชาติมาก จริงๆ ต้องบอกว่าการคิดแบบ loop ตั้งหากที่ขัดกับความคิดของคน

เช่น ถ้าจะสั่งให้คนทาสีห้อง วิธีการที่คนจะสอนงานก็จะออกมาในรูปแบบ "เอาแปรงทาสีจุ่มในถังสีแบบนี้นะ ปาดสีออกอย่าให้เยิ้มเกินไป ทาลงผนังแบบนี้ๆ" แล้วจบด้วยคำว่า "ทาไปเรื่อยๆ จนกว่าจะเต็มทั้งผนังนะ"

นั่นแหละ คือการกำหนดวิธีแก้ปัญหาแบบ 1 หน่วย (Terminate Case) แล้วก็ปล่อยพนักงานทาไปเรื่อยๆ (พนักงานอาจจะไปตามเพื่อนมาช่วยก็ยังได้ แต่ทำด้วยวิธีเดียวกัน)

วิธีการฝึกการเขียน Recursive ก็ไม่ยาก ให้ลองแปลงโค้ดที่คุณเคยเขียนในรูปแบบ loop ให้เป็น Recursive ให้ได้โดยที่ output ต้องออกมาแบบเดิมด้วยนะ ฝึกไปเรื่อยๆ ก็จะชินกับมันเอง

เรื่องของ Recursive จริงๆ ยังไม่จบเท่านี้ ในบทต่อไป เราจะมาพูดถึงข้อดีข้อเสียของการใช้งาน Recursive ในเครื่องคอมพิวเตอร์ที่สร้างมาแบบ Imperative กัน รวมถึงวิธีการที่เรียกว่า Tail Call Optimization หรือการจัดการหน่วยความจำไม่ให้ Recursive Function มันกินเมโมรี่จน overflow!