Think Recursive

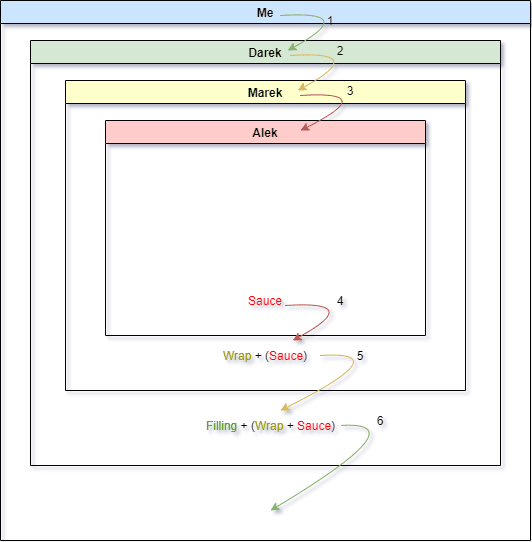
I am not so good at cooking stuff but I am an all time admirer of the traditional Polish dish 'Pierogi'. I took a few days off from work last week, all determined not to let the days fly by without getting my hands on the polish delicacy. Now I do realize that I don't even know where to start from. Well, what are friends for? Now read this with patience! I made a call to "Darek" back in Warsaw and asked him if he could give me some direction. Darek, being just another geek, told me that he knows how to do the veggies (the filling) but then he shall ask another friend, how to prepare the wrap. He put me on hold and went ahead to call his friend, Marek. Marek tells Darek that he does indeed know how to do the wrap but then he shall call Alek, who lives nearby to find out how to do the dressing. 'Sauce', my friends, is important. He puts Darek on hold as well. Silly! Alright so Alek, the neighbor finally does't call another friend but gives away the recipe of the sauce. Marek combines his recipe of the wrap with what Alek told him about the sauce and conveys it back to Darek, who was simply waiting to combine this information with the recipe of the filling only to deliver the complete information back to me. Long day but I finally have what I needed.

let alek = { name: 'Alek', friend: null, ingr: 'sauce', done: true };

let marek = { name: 'Marek', friend: alek, ingr: 'wrap' };

let darek = { name: 'Darek', friend: marek, ingr: 'filling' };

function getRecipeHelp(friend) {
  if(friend.done) {
    // bail out condition
    return friend.ingr;
  }
  return friend.ingr + ' + ' + getRecipeHelp(friend.friend);
}

// Here we call Darek to get help with the recipe who then calls his friend Marek and Marek finally calls his friend Alek
console.log(getRecipeHelp(darek)); // "filling + wrap + sauce"

Assuming you digested the example really well, let me now ask you, how do you think you'd define 'recursion'? The academic definition says 'A non leaf function calling itself'. On a personal note, I understand recursion as a quest to meet the bail out condition so that the return values can sequentially be resolved into the final output. This may confuse you a little unless you understand that every recursive function you define has to have a bail out condition. Broadly, I'd recommend you to remember three things about any recursive function. What are those three things?

1. You should start with thinking of the bail out condition
2. Understand that the values start resolving in LIFO fashion to finally render the output
3. Recursively call the function itself but with a different argument ofcourse ( Make sure you'e moving towards the bail out condition)

Though the bail out condition is quite visible in the example, to make it even more clear, if you do not have this check to stop your recursive calls, you may end up with a stack overflow where functions keep piling up on the stack without returning. By value resolution in LIFO fashion, all I mean is that the functions lower in the stack keep waiting until the final function (that satisfies the bail out condition) returns some decreed value, post which the return values start getting resolved top to bottom in the stack. With so much of this information at hand, go ahead and try implementing the classic factorial function.

function factorial(n) {
  if(n<2) {
    // bail out condition
    return 1;
  } 
  // make sure you're moving towards the bail out condition and not away from it
  return n * factorial(n-1);
}

I think the illustration is self explanatory. If not, lets cover another example. Lets get the fibonacci series in. Hardly anyone in the wild, would be unaware of the fibinacci series but still it goes like this 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.. Every other number starting from the third in series is the sum of the previous two. Fibonacci is magical, go ahead and read this.

// 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... starts with 0 and 1 and then each number is the sum of previous two numbers in the series

function fib(n) {
  return n <= 1 
  ? n // bail out condition
  : fib(n-1) + fib(n-2); // make sure you're moving towards the bail out condition and not away from it
}
console.log(fib(10)); // 55

Conceptually, not much different from what we did for factorials. Think of every recursive function as a mathematical function. Perhaps then it shall become more obvious. We've got our bail out condition at (n <= 1) , where we simply return any argument that's less than 1. Otherwise we go ahead and make recursive calls to the fib function for n-1 and n-2. Well, that only gives me the nth fibonacci member. How'd you print the entire series? Try not to use loops and create a recursive function showFib(n) {..} that prints the series all at once. Here's the code.

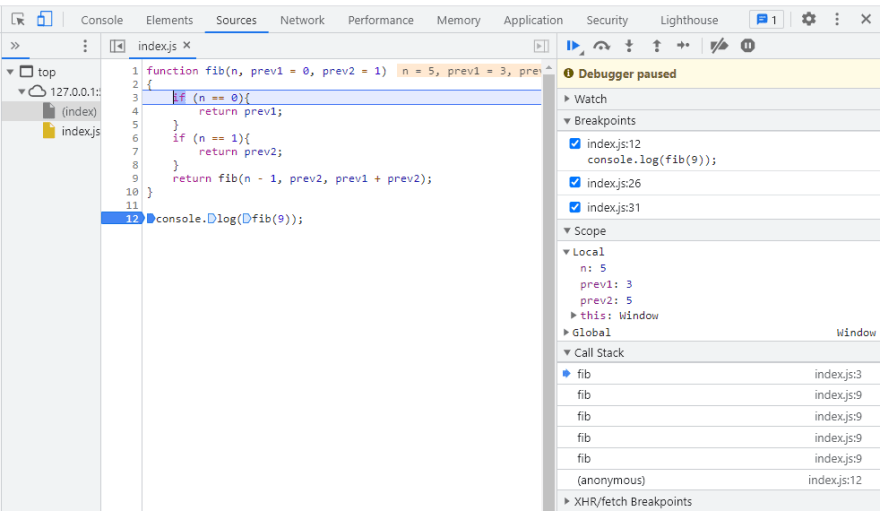
Alright! now try calling the fib(n) function like fib(999999) or fib(9999999). Do you see the result already? As you could say just by looking at it, its going to be a huge huge number, your browser may give up on this and start crawling or you may even get a stack overflow exception depending on the content in the call stack. Switch back to the illustration that shows the stack for the factorial program. Can you imagine 999999 functions being piled up all waiting for their successor to return some value? How do you get around this? There's actually a way out but that's kind of a trade off. We call it Proper Tail Calls (PTC). Checkout the last line in the function. For the factorial function its a return statement. The return statement has two parts if you see

1. a multiplier i.e. n
2. a recursive call i.e. factorial(n-1)

Since we have the multiplier waiting for the recursive call to return some value, the function cannot be offboarded from the stack. It has this pending work (multiply by n) to finish after the recursive call returns. What if we pass the product to the recursive call instead of waiting with the multiplier? Well, since the pending work will get delegated to the recursive call everytime , the engine won't need to keep the execution stack crowded with functions in stand by.

function factorial(n, product = 1) {
  return n < 1
  ? product
  : factorial(n-1, n * product);
}

console.log(factorial(99)); // 9.332621544394415e+155
console.log(factorial(999)); // Infinity
console.log(factorial(999999)); // Error- Maximum call stack size exceeded 

You see it works better now. Unlimited frames and you can call a function recursively as many times as you want? Before mentioning PTC, I said it was a tradeoff. A tradeoff with the stack trace. You no longer have easy debugging for your function. Since the function frame is lost to create space in the execution stack, they won't show up even while tracing your error. Read more here. So hold your horses and think before you opt for an optimized recursive solution. Now you're thinking, won't it misfire everytime you place a function call in the tail of a function? You don't want to lose the stack trace. Good news and Bad news, all that I told you about Proper Tail Calls simply won't work with JS engines other than JavaScriptCore (by Apple). Apple likes to call it Tail Call Optimization (TCO). TCO goes one step ahead of PTC to actually optimize your function execution.V8 did infact support this for a while but then for the same reason and possibly some bugs, took it down. If you are on chrome, you can test this out in your debugger. Alternatively you can go through this. V8 creates frames for all function calls and keeps them in the stack regardless of the way you write your code. So you still get the stack overflow exception if you take your recursions off limit. An explicit version of PTC is under discusstion (seems abandoned though). They call it Syntactic Tail Calls (STC).

Originally Posted Here -

https://mayankav.webflow.io/blog/think-recursive