While there are numerous online sources that cover this topic, I aim to offer an uncommon approach by developing an algorithm for the AI player that closely mimics human thinking.
Let's begin by introducing some notation that will be used throughout the article. The grid consists of 9 cells, each assigned a numbered position as follows:
The center cell is denoted as 4, the corner cells are 0, 2, 6, and 8, and the edge cells are 1, 3, 5, and 7. Although the starting symbol is irrelevant for the algorithm, for the sake of this article, we will assume that X always makes the first move.
In a game played perfectly by both players, it results in a draw. However, when players are not flawless, the one with the best chances of winning is the player capable of creating a fork. A fork occurs when a player reaches a board state where they can create three-in-a-row in two different ways on their next move, making it impossible for the opponent to defend. This is an example situation where X is about to win, regardless of O's move on their current turn.
Enumerating All Board States
This section is not essential for understanding the main subject of this article, which focuses on constructing the AI player. Its purpose is to provide insights into the scale of the problem.
Tic-tac-toe is a relatively simple game, and it is feasible to enumerate all possible board states. One approach is to store the states in a lookup table or a hash map, where each state is associated with the optimal move for the player. For instance, in the following scenario, the best move for X is to play at position 3, thereby blocking O from winning in the next move.
To represent this information in a hash map, we can use a key representing the board state, such as "..o.x.x.o", and the corresponding value representing the best position to play, in this case, 3.
Determining the best move for each board state can even be analyzed manually.
Now, let's explore the feasibility of this approach by calculating the total number of possible board states.
Suppose we have made moves so far, which implies that there are X's and O's on the board. For the symbols, we can choose cells out of the total 9 in ways. Then, we can arrange O's into the selected cells, resulting in possible arrangements. This gives us a total of
distinct board configurations with symbols.
For example, how many board states are there with 5 symbols? Choosing 5 cells out of 9, and then arranging 2 O's into those 5 cells, gives us
different board states.
Since there can be any number of symbols between 0 and 9, we have
different board configurations in total.
However, this is an upper bound, as not all of these states are valid. For instance, consider the following board state included in the above calculation:
This state is clearly invalid because there is no point in continuing the game after one of the players has already won, and it appears that both players have achieved a three-in-a-row.
Furthermore, we can reduce the number of states that need to be stored by excluding rotations and reflections. For example, the following 8 states are equivalent, and knowing the best move for one of them is sufficient to determine the best move for all of them.
Each state belongs to a group of at most 8 equivalent symmetrical states. By considering this into the analysis, the number of states requiring storage can be significantly reduced, nearly by a factor of 8.
Additionally, there is no need to save winning states or states with a full grid of 9 symbols. These are considered end states where the game cannot progress any further.
There are a few more optimization techniques that can further reduce the number of states. By incorporating all of these ideas, the total number of states can be reduced to approximately 600. This number of states makes it manageable even for manual analysis.
Finding the Optimal Strategy
A skilled human player typically follows this approach on each move:
- if there is a winning move, play it
- if there is a move that blocks the opponent's potential win, play it
- if there is a possibility to make a fork, do it
- if there is a possibility to do an attack, do it
This outline serves as the basis for our AI algorithm. However, it doesn't provide a solution for every board state, particularly at the beginning of the game. The plan is to apply this algorithm to every feasible board state and refine it where it falls short.
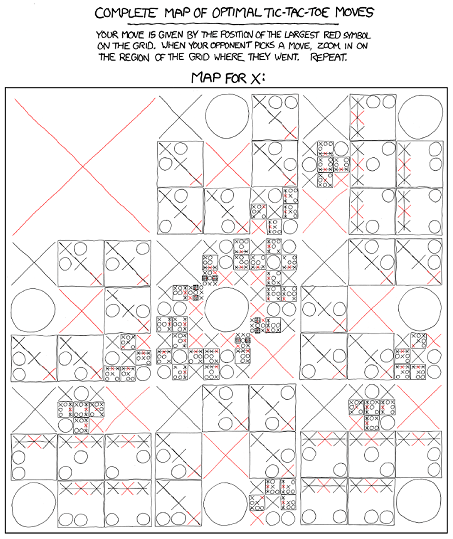
There is an xkcd comic that visually depicts the optimal play. The representation for player X can be seen here:
The representation for player O is similar but slightly more complex.
The image displays the best moves for all reachable board states. By carefully applying the above algorithm to each board state in the image, removing solvable states, and eliminating duplicates through equivalent rotations and reflections, we are left with only 13 unresolved board states:
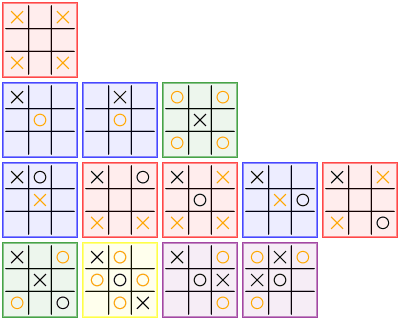
It's worth noting that each of these unresolved board states contains a maximum of three symbols. The next step involves analyzing each of them to identify all viable moves. Here is the resulting chart:
The orange symbols indicate the best moves. It is apparent that there are multiple equally good moves for nearly all of these board states. By utilizing this chart and the above algorithm, one can determine the ideal course of action and play a perfect game until the end.
The final step is to enhance the algorithm with additional rules based on this chart, while striving to keep them as straightforward as possible. Let's incorporate these rules. The revised pseudocode is as follows:
- if there is a winning move, play it
- if there is a move that blocks the opponent's potential win, play it
- if number of symbols < 4:
- if it’s player 1’s turn and edges are empty, take any corner # red
- if player 2 has the center:
- if an edge is taken, take any corner adjacent to it # purple
- else take any edge # yellow
- take the center if available # blue
- take any corner # green
- if there is a possibility to make a fork, do it
- if there is a possibility to do an attack, do it
- play anything
Note: The additional rules are annotated with colors at the end of lines, corresponding to the board states they address in the following chart. Some of the orange symbols representing the best moves are removed from the chart to align with the rules in the pseudocode.
This revised pseudocode now provides a complete definition for our AI player. It can also be followed by a human player.
Board Representation in Code
A wide range of programming languages can be used for implementation. I have implemented this logic in both Python and JavaScript, and in this article, I will present the Python version.
When implementing this algorithm, it's crucial to decide how to represent the board state. One common approach is to use a matrix (an array of arrays) or a string. However, I have chosen to represent it as a binary number to optimize performance through efficient bit manipulations. While this may not be necessary for such a simple game, it's still a fun exploration.
In this representation, X is player 1, O is player 2, and 0 denotes an empty cell. Each cell can have a value of 0, 1, or 2, requiring only 2 bits to represent. Taking the example board state:
We can assign values as follows:
By ordering these digits, we obtain the binary number that represents this board state: 01 01 00 00 10 01 00 10 00.
In Python, we can directly save this state using 0b numeric literals. To improve readability, Python allows the use of underscores to visually separate digits. Therefore, we can save the above board state as:
board = 0b_01_01_00_00_10_01_00_10_00
Now, let's explore some examples of using bitwise operations on this board state.
To extract the symbol at position p, we can use:
symbol = board>>2*p & 0b11
This operation shifts the board to the right by 2*p bits, placing the desired symbol in the rightmost position, and then extracts those two bits using bitwise AND with 0b11.
To create a new board state after a player makes a move at position 6, we can use:
new_board = board | player<<2*6
Here, the player value is shifted to the left by 2*6 bits and then combined with the board using bitwise OR.
Now, let's also explore counting the number of symbols on the board. This task involves slightly more complexity. Assuming a valid board state, our goal is to count the number of set bits. We can achieve this by implementing the following function:
def count_symbols(board):
count = 0
while board:
board &= board-1
count += 1
return count
To understand the logic behind it, let's break down the first iteration of the loop using our previous example.
board = 01 01 00 00 10 01 00 10 00
board-1 = 01 01 00 00 10 01 00 01 11
------------------------------------
board = board & board-1 = 01 01 00 00 10 01 00 00 00
By performing the bitwise AND operation between the board and board-1, we effectively remove the rightmost set bit. Continuing this process until we are left with an empty board will result in iterating count times, which corresponds to the number of set bits.
We will use the function count_symbols in our implementation below.
These examples provide insight into the implementation, showcasing the utilization of bitwise operations and the chosen binary representation of the board.
Implementation
Let's gradually construct the main function find_best_move.
def find_best_move(board, player):
# find winning move
# find blocking move
# handle if less than 4 symbols:
if count_symbols(board) < 4:
# if it's player 1's turn and edges are empty, take any corner
# if player 2 has the center:
# if an edge is taken, take any corner adjacent to it
# else take any edge
# take the center if available
# take any corner
pass
# find a fork
# find an attack
# play any move
This function accepts the current state of the board and the player who is currently making a move. Its objective is to return a new state of the board.
First, let's create a function that handles playing any move. This function will be placed directly at the bottom of our logic. We will design it to accept a list of permissible positions, which will prove useful later on.
def find_available(board, player, allowed):
for p in allowed:
if board & 0b11<<2*p == 0:
return board | player<<2*p
The purpose of this function is to locate any vacant position from the provided allowed list of cells and return the updated board with the new symbol in place. To execute any move, we simply need to provide the list [0, 1, 2, 3, 4, 5, 6, 7, 8] as allowed positions. For instance, if we wish to play a move in any of the corners, we can provide the list of corner positions as [0, 2, 6, 8].
Now that we have the find_available function ready, let's proceed to implement the logic for when the symbol count is less than 4.
To check if the edges are empty, we use the following code:
if not board & 0b_00_11_00_11_00_11_00_11_00
To determine if player 2 has the center:
if board & 0b_00_00_00_00_10_00_00_00_00
To test whether an edge is already taken and to place the symbol adjacent to that edge, we can achieve this in just two lines of code. Check if any edge in positions 1 and 3 is occupied and play on the corner between them. Otherwise, check edges 5 and 7 and play in corner 8.
if board & 0b_00_00_00_00_00_11_00_11_00: return board | player
if board & 0b_00_11_00_11_00_00_00_00_00: return board | player<<16
Now we have all the components necessary to assemble the part for when there are fewer than 4 symbols on the board.
def find_best_move(board, player):
# find winning move
# find blocking move
# handle if less than 4 symbols:
if count_symbols(board) < 4:
# if it's player 1's turn and edges are empty, take any corner:
if player==1 and not board & 0b_00_11_00_11_00_11_00_11_00:
return find_available(board, player, [0, 2, 6, 8])
# if player 2 has the center:
if board & 0b_00_00_00_00_10_00_00_00_00:
# take any corner adjacent to a taken edge:
if board & 0b_00_00_00_00_00_11_00_11_00: return board | player
if board & 0b_00_11_00_11_00_00_00_00_00: return board | player<<16
# take any edge:
return find_available(board, player, [1, 3, 5, 7])
# take the center if available, or take any corner:
return find_available(board, player, [4, 0, 2, 6, 8])
# find a fork
# find an attack
# play any move:
return find_available(board, player, [0, 1, 2, 3, 4, 5, 6, 7, 8])
Let's continue with the logic for finding a winning move. To accomplish this, we will define masks that will be used for checking three-in-a-row combinations. There are 8 masks in total, representing the 8 different possibilities for achieving three-in-a-row.
win_masks = [
0b_01_01_01_00_00_00_00_00_00,
0b_00_00_00_01_01_01_00_00_00,
0b_00_00_00_00_00_00_01_01_01,
0b_01_00_00_01_00_00_01_00_00,
0b_00_01_00_00_01_00_00_01_00,
0b_00_00_01_00_00_01_00_00_01,
0b_01_00_00_00_01_00_00_00_01,
0b_00_00_01_00_01_00_01_00_00
]
Now, let's define a function that attempts to find a winning move. If a winning move exists, the function will return the new board state.
def find_winning_move(board, player):
for mask in win_masks:
mask *= player
new_board = board | mask
if is_valid_board(new_board) and are_successive_boards(board, new_board):
return new_board
In this code snippet, we iterate through each winning mask. In the case of player 2, we need to adjust the masks by multiplying them by the value 2, effectively shifting the bit mask one place to the left. For each mask, we perform a bitwise OR operation with the board to obtain the new board state. If this new board is considered valid (i.e., no overlapping X's and O's) and if it has exactly one more symbol than the original board, we have found a winning move.
Now, let's discuss the two auxiliary functions: is_valid_board and are_successive_boards.
def is_valid_board(board):
# check for broken cells (overlapping X and O):
return not board & board>>1 & 0b_01_01_01_01_01_01_01_01_01
def are_successive_boards(b1, b2):
b = b1 ^ b2
return b>0 and not b & b-1 # is not 0 and is power of 2
To explain the check for overlapping cells, let's consider the example of a single cell. A cell can be in one of three valid states: 0b00, 0b01, and 0b10. To check for the only invalid state, 0b11, we can take the state and bitwise AND it with itself shifted one place to the right. If the rightmost bit becomes 1, it indicates that the state is invalid. The left bit is not relevant for this check, so we ensure it is unset by performing a bitwise AND with 0b01. By applying this operation to all cells simultaneously, we can check for overlapping X's and O's on the whole board.
The function are_successive_boards is used to determine if two boards are successive. We calculate their difference using bitwise XOR and check if the result contains only one symbol. This condition effectively means that the board is a number that is a power of 2. For this check to work correctly, both boards need to be valid.
Let’s continue with finding a blocking move. This involves identifying if there exists a winning move for the opponent. We can make use of the find_winning_move function by passing the opponent as a parameter. If a winning move is found, we can simply swap the opponent's winning symbol.
def find_blocking_move(board, player):
b = find_winning_move(board, 3-player) # find winning move for the opponent
if b:
c = board ^ b # get only the last symbol on the board
c = c>>1 if player==1 else c<<1 # swap the symbol
return board | c # put the symbol back
Now, let's create a function for finding an attack. Finding an attack means identifying a move that leads to a board state that creates an opportunity to make three-in-a-row in the next turn. To find such a move, we iterate over each available cell and, for each resulting board state, check if a winning move can be found for the same player.
def find_attack(board, player):
for p in range(9):
if board & 0b11<<2*p: continue # this cell is taken
b1 = board | player<<2*p
if find_winning_move(b1, player):
return b1
Lastly, we need to address the problem of finding a fork. The solution is slightly more complex than finding an attack. The main difference is that when searching for a winning move, we need to ensure that the move can be confirmed using two different masks. To accomplish this, we unpack the find_winning_move function and make a small adjustment: whenever we find a winning move with one mask, we continue searching for a winning move with different masks. If we find two masks that confirm the same winning move, we have discovered a fork.
def find_fork(board, player):
fork_board = None
for p in range(9):
if board & 0b11<<2*p: continue # this cell is taken
b1 = board | player<<2*p
for mask in win_masks:
mask *= player
b2 = b1 | mask
if is_valid_board(b2) and are_successive_boards(b1, b2):
# if already found another attack with b1, then this is a fork:
if fork_board == b1: return b1
fork_board = b1
To simplify the overall logic, we can combine the find_attack and find_fork functions into a single function called find_best_attack. This function attempts to find a fork first. If no fork is found, it returns the last attack that was discovered. The best_new_board variable stores the most recent attack found.
Let’s rename and modify the function accordingly.
def find_best_attack(board, player): # find a fork if exists, else find any attack
best_new_board = None
for p in range(9):
if board & 0b11<<2*p: continue # this cell is taken
b1 = board | player<<2*p
for mask in win_masks:
mask *= player
b2 = b1 | mask
if is_valid_board(b2) and are_successive_boards(b1, b2):
# if already found another attack with b1, then this is a fork:
if best_new_board == b1: return b1
best_new_board = b1
return best_new_board
With these components in place, we now have all the necessary pieces to complete the main function.
def find_best_move(board, player):
# find winning move:
if b := find_winning_move(board, player): return b
# find blocking move:
if b := find_blocking_move(board, player): return b
# handle if less than 4 symbols:
if count_symbols(board) < 4:
# if it's player 1's turn and edges are empty, take any corner:
if player==1 and not board & 0b_00_11_00_11_00_11_00_11_00:
return find_available(board, player, [0, 2, 6, 8])
# if player 2 has center:
if board & 0b_00_00_00_00_10_00_00_00_00:
# take any corner adjacent to a taken edge:
if board & 0b_00_00_00_00_00_11_00_11_00: return board | player
if board & 0b_00_11_00_11_00_00_00_00_00: return board | player<<16
# take any edge:
return find_available(board, player, [1, 3, 5, 7])
# take the center if available, or take a corner:
return find_available(board, player, [4, 0, 2, 6, 8])
# find a fork, or else any attack:
if b := find_best_attack(board, player): return b
# play any move:
return find_available(board, player, [0, 1, 2, 3, 4, 5, 6, 7, 8])
Sometimes, there are situations where we want the AI to play on any available corner, but the current code always selects the first available corner from the list of allowed positions. To introduce some randomness in the AI's moves when multiple moves are equally good, we can shuffle the list of allowed positions. This way, the AI won't always make the same move.
Implementing the shuffle functionality is fairly simple. We can utilize the random.shuffle() function that shuffles the list in-place.
import random
def shuffle(a):
random.shuffle(a)
return a
With the shuffling capability added, unnecessary comments removed, and final adjustments made to our main function, we have completed our AI tic-tac-toe solution.
def find_best_move(board, player):
if b := find_winning_move(board, player): return b
if b := find_blocking_move(board, player): return b
if count_symbols(board) < 4:
if player==1 and not board & 0xCCCC: # edges empty
return find_available(board, player, shuffle([0, 2, 6, 8]))
if board & 0x200: # player 2 has center
if board & 0x00CC: return board | player
if board & 0xCC00: return board | player<<16
return find_available(board, player, shuffle([1, 3, 5, 7]))
return find_available(board, player, [4] + shuffle([0, 2, 6, 8]))
if b := find_best_attack(board, player): return b
return find_available(board, player, shuffle([0, 1, 2, 3, 4, 5, 6, 7, 8]))
Repository
The implementations of this algorithm in both Python and JavaScript, along with the script that helped create SVG images used in this article, can be found in this repository.








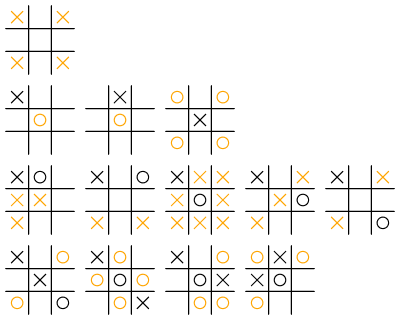







Top comments (1)