The Laplace transform was named after Pierre Simon De Laplace (1749-1827), a prominent French mathematician. Like any other transform, the Laplace transform converts one signal into another using predetermined rules or equations. Utilizing the Laplace transformation is the best approach to translating differential equations into algebraic equations.
Laplace transform is essential in the design of control systems. It is necessary to perform Laplace transforms on several functions to analyze the control system. The Laplace transform and its inverse are utilized in the dynamic control system's analysis for their respective qualities. In this post, we'll dive deep into the laplace transform in MATLAB.
What is the Laplace Transform?
A function must have infinitely many discontinuities to be considered piecewise continuous without ever expanding to infinity. The Laplace transform defines the function f(t) if it is assumed that f(t) is a piecewise continuous function. We use Lf(t) or F. (s) to express a function's Laplace transform. When a differential equation is reduced to an algebraic issue, the Laplace transform aids in its solution.
It's a way to show a function, which (usually) has a value of 0 for time <0, as the accumulation of several waves that resemble:
Remember that what I just mentioned isn't accurate because there's also a fictional component in this situation, and we're integrating.
Laplace Transform Formula
The Laplace transform takes a derivative function in a real variable t and transforms it into a complex function in a real variable s. For example, let f(t) be given for t 0 and suppose that the function meets some later-explained requirements.
The formula for the Laplace transform of f(t), represented by Lf(t) or F(s), is as follows:
every time the erroneous integral converges.
The Laplace transform is denoted by an uppercase letter in cases where the notation is evident, as in L(f; s) = F. (s).
The one-sided Laplace transform is another name for the Laplace transform that we defined. A two-sided version exists with the integral changing from to.
Math
It is an attempt to illustrate the operation of the Laplace Transform:
When performing this, it is necessary to examine the inverse Laplace Transform's definition:
While attractive, it's not the best to work with, therefore let's use the alternative:
so that our new limits are just \infty to -\infty, and ds\dr = j giving:
Which approximately translates as:
Laplace Transform Table
The engineer always has access to a table detailing Laplace transforms and the data they require. The following is an illustration of a Laplace transform table. The following table will provide information on the Laplace transform for several popular functions.
Method of Laplace Transform
The Laplace transformation is crucial to the design of control systems. To research a control system, we must do the Laplace transform on each function (function of time). A crucial technique for determining the function f(t) from its Laplace form is the Inverse Laplace. Inverse and Laplace transforms have specific characteristics when evaluating dynamic control systems.
Differentiation, time scaling, integration, conjugation, multiplication, convolution, frequency shifting, time shifting, and periodic function are all examples of linearity. Concerning control systems, there are two key theorems. They are:
- Initial value theorem (IVT)
- Final value theorem (FVT)
Several functions are subjected to the Laplace transform, including the Bessel function, unit impulse, ramp, step, sine, unit step, cosine, shifted unit step, hyperbolic sine, exponential decay, and hyperbolic cosine. However, the Laplace transform's most significant benefit is its ability to quickly and accurately solve higher-order differential problems by transforming them into algebraic equations.
The Laplace transform of a time function requires a specific sequence of operations. To convert a given time function f(t) into its equivalent Laplace transform, we must first do the following steps:
- F(t) is first multiplied by e-st, where s is a complex number (s = + j).
- Integrate this product with respect to time, using the limits of zero and infinite. It incorporation outcomes in Laplace transformation of f(t), which is indicated by F(s).
The technique by which the time function f(t), indicated by £-1, is recovered from the Laplace transform is known as the inverse Laplace transformation.
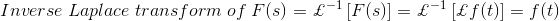
Applications of Laplace Transform
- It is used to simplify complicated differential equations by adding polynomials.
- Derivatives can be transformed into polynomials over a wide range of domain variables, and then the inverse Laplace transform can be used to return to the original differential equation.
- It is employed in telecommunications to transmit signals to both ends of a channel. For instance, when signals are transmitted over a phone line, they are first transformed into a time-varying wave before being superimposed on the medium.
- It is also utilized for various technical activities, including system modeling, digital signal processing, and electrical circuit analysis.
Top comments (0)