Resources
- Find the Github link here
AST
We now need to define a structure which our interpreter will use to store and evaluate the mathematical expressions. In our case we will form a Bottom-Up Evaluation more details when we get to Parsing in the next chapter.
If you can recall our ast structure in Part 1
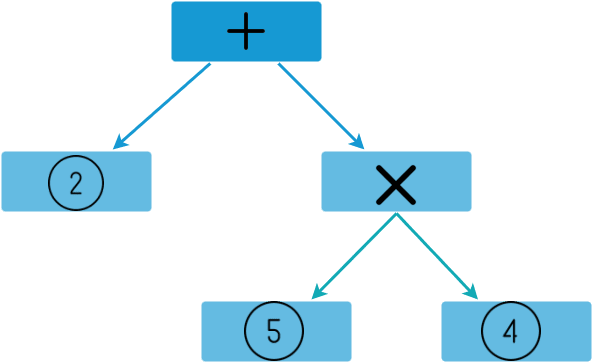
We're going to form an AST structure of the following form
ASTPlus(Leaf(2),
ASTMult(Leaf(5), Leaf(4)))
Simply to put it, our AST will have Leaf Nodes which will hold numeric value, ASTPlus and ASTMult will hold objects of type Leaf Node or Other ASTs.
Init
Let's start by creating a class, let's call it: AST.cs.
We can go ahead and make the class generated an Abstract class, then lets add an abstract method Eval which will allow us to recursively evaluate expressions
public abstract class AST
{
public abstract decimal Eval();
}
Now right below this class lets define a leaf node which inherits from AST abstract class and implements the abstract method.
We also know our leaf nodes will only hold numerical values so we can design the class like so.
public class ASTLeaf : AST
{
public readonly decimal _num;
public ASTLeaf(decimal num)
{
this._num = num;
}
public override decimal Eval()
{
return this._num;
}
public override string ToString()
{
return this._num.ToString();
}
}
Lets create another class right below this ASTLeaf and call it ASTPlus. It will hold the addition objects.
public class ASTPlus : AST
{
public readonly AST _leftNode;
public readonly AST _rightNode;
public ASTPlus(AST leftNode, AST rightNode)
{
this._leftNode = leftNode;
this._rightNode = rightNode;
}
public override decimal Eval()
{
// Perform the evaluation
return this._leftNode.Eval() + this._rightNode.Eval();
}
public override string ToString()
{
return String.Format("({0} + {1})", this._leftNode.ToString(), this._rightNode.ToString());
}
}
In our class ASTPlus we are taking in two AST objects, this could be any class. Implementing it in this approach allows us to implicitly have any class as long as it implements AST.
Our Eval method returns the sum of the evaluations of the AST objects. So, this means be it ASTMinus or ASTLeaf we will be calling the Eval method from the class objects first before we sum them up in ASTPlus
We have added the ToString method override, this will allow us to view the evaluation heirachy.
The same class structure goes for ASTMinus, ASTMultiply and ASTDivide. Just remember to change the operation sign in the Evaland ToString methods.
So our final AST.cs class will look like so.
public abstract class AST
{
public abstract decimal Eval();
}
public class ASTLeaf : AST
{
public readonly decimal _num;
public ASTLeaf(decimal num)
{
this._num = num;
}
public override decimal Eval()
{
return this._num;
}
public override string ToString()
{
return this._num.ToString();
}
}
public class ASTPlus : AST
{
public readonly AST _leftNode;
public readonly AST _rightNode;
public ASTPlus(AST leftNode, AST rightNode)
{
this._leftNode = leftNode;
this._rightNode = rightNode;
}
public override decimal Eval()
{
// Perform the evaluation
return this._leftNode.Eval() + this._rightNode.Eval();
}
public override string ToString()
{
return String.Format("({0} + {1})", this._leftNode.ToString(), this._rightNode.ToString());
}
}
public class ASTMinus : AST
{
public readonly AST _leftNode;
public readonly AST _rightNode;
public ASTMinus(AST leftNode, AST rightNode)
{
this._leftNode = leftNode;
this._rightNode = rightNode;
}
public override decimal Eval()
{
return this._leftNode.Eval() - this._rightNode.Eval();
}
public override string ToString()
{
return String.Format("({0} - {1})", this._leftNode.ToString(), this._rightNode.ToString());
}
}
public class ASTMultiply : AST
{
public readonly AST _leftNode;
public readonly AST _rightNode;
public ASTMultiply(AST leftNode, AST rightNode)
{
this._leftNode = leftNode;
this._rightNode = rightNode;
}
public override decimal Eval()
{
return this._leftNode.Eval() * this._rightNode.Eval();
}
public override string ToString()
{
return String.Format("({0} * {1})", this._leftNode.ToString(), this._rightNode.ToString());
}
}
public class ASTDivide : AST
{
public readonly AST _leftNode;
public readonly AST _rightNode;
public ASTDivide(AST leftNode, AST rightNode)
{
this._leftNode = leftNode;
this._rightNode = rightNode;
}
public override decimal Eval()
{
return this._leftNode.Eval() / this._rightNode.Eval();
}
public override string ToString()
{
return String.Format("({0} / {1})", this._leftNode.ToString(), this._rightNode.ToString());
}
}
So now we have an AST structure that will hold our expressions.
In the next chapter we are going to;
- Create a Parser -> Expression, Factor and Term
- Implement Eval
- Write Tests



Top comments (0)