Originally posted at ellehallal.dev👩🏽💻
This week, I have been working on adding an unbeatable computer (UC) player to my Ruby Tic Tac Toe game.
In this blog, I will share my understanding of recursion and minimax, and my first attempt at using it to create an unbeatable computer player. In order to implement a UC Player I needed to implement the MiniMax algorithm, which also meant I needed to use recursion.
The computer player
The beatable computer player
Before working towards making it unbeatable, the computer player selected a move without a strategy. It simply picked an available space on the Tic Tac Toe board at random.
The unbeatable computer (UC) player
The UC player should know the available squares on the board, assess all of the possible outcomes and as a result, choose the best move.
What is considered to be the best move?
The UC player’s aim is to win. If this is not possible, the next best outcome for the UC is for the game to be a tie. The opponent winning the game is not an option. A move should be selected to prevent an opponent from winning, subsequently resulting in a win or a tie for the UC player.
Recursive functions and Minimax
What is a recursive function?
My understanding of a recursive function is a function which calls itself, until a certain condition is met. It consists of a base case, and a recursive case.
Base case: when triggered, this stops the recursive function.
Recursive case: The recursive function calls itself again, with a slight variation from the previous function call. The recursive case occurs when the base case is not triggered.
What is the minimax algorithm?
My understanding is:
it’s an algorithm which uses recursion
the aim is to maximise the outcome for active player and conversely minimise the outcome for the other player
it is used to get the optimum move for a player in a game
it plays out all of the possible outcomes, using the current player and opponent mark
each outcome of the game is given a score, depending on whether the current player wins, an opponent wins, or the game is a tie.
the selected move should minimise the points the opponent can obtain.
In the context of a Tic Tac Toe game:
The maximising player is the UC player, and the minimising player is the opponent.
The base case is triggered when either player has a winning line or the board is full (a tie).
If the base case is not triggered, the recursive function will continue where the UC player’s mark and the opponent’s mark will keep being added to the available squares on a board
When a mark is added to the board, this means the recursive function has been called again.
When a player has won, or the game is a tie, the initial square that was played is given a score.
The UC player selects the best move where the opponent’s score is minimised.
How is an outcome scored?
If the game is a tie, the outcome is scored as 0. The maximum points a winning player can obtain is 10 (or -10 in the case of an opponent).
As a mentioned above, when a mark is added to the board, the recursive function is being called again. My understanding is by keeping track of the depth (how many times the recursive function has been called), this helps to assess the outcome of the game. The aim is to win in the fewest moves. Therefore a win in 1 move should have a higher score than a win in 3 moves
As a mark is added to the board (another recursive function call, increase in depth by 1), the depth is subtracted from the player’s maximum score.
For example, here’s a scenario:
The UC player is looking for the best move and tries out position 3
After the recursive function was called 3 times (
depth = 3), the UC obtained a winning line
maximum_score = 10
depth = 3
score = maximum_score - depth
#score = 7
A Visual Example Of The UC Player Using Minimax
Expanding on the above, the example below presents a scenario where the UC player has three available squares it can choose from (3, 4, and 9). It demonstrates all of possible outcomes being played.
The UC player (x) is the maximising player, and the opponent (o) is the minimising player. I’ll explain all of the possible outcomes in more detail below.
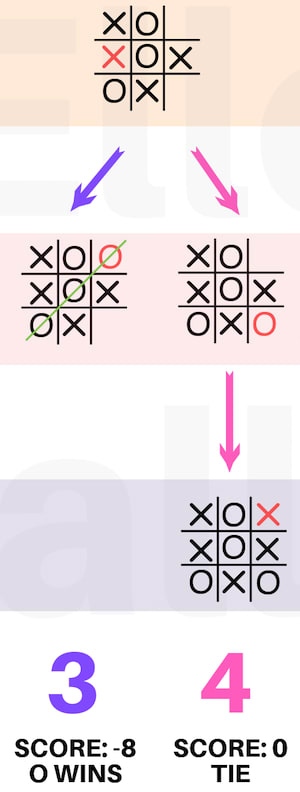
The UC playing position 3
The image above demonstrates the following:
UC plays position 3 (depth 1)
Opponent plays position 4 (depth 2)
UC plays position 9 (depth 3)
The outcome is a winning line for the UC, after a total of 3 positions have been played.
The UC has won, so the maximum score is 7. Remember the maximum points the UC can get is 10, and the depth is subtracted from this.
To the right of the image:
UC plays position 3 (depth 1)
Opponent plays position 9 (depth 2)
UC plays position 4 (depth 3)
The outcome is tie, neither the UC or the opponent has a winning line. The minimum score is 0.
In conclusion, for position 3:
Maximum score = 7 (10–3)
Minimum score = 0 (tie)
The UC playing position 4
In the above diagram, the UC plays position 4. When doing this, both outcomes result in the UC not winning, and the opponent wins in one.
In conclusion, for position 4:
Maximum score = 0 (tie)
Minimum score = -8 ( -(10–2))
The UC playing position 9
The maximum score is 7 , as the UC can win in one of the outcomes at depth 3.
However, the minimum score is -8 , because the opponent wins in the other outcome at depth 2.
Although the UC can win by choosing position 9, the opponent can win on the next move.
In conclusion, for position 9:
Maximum score = 7 (10–3)
Minimum score = -8 ( -(10–2))
Using the scores to select a best move
My understanding is the UC player’s aim is to ensure the opponent obtains the minimum amount of points possible. The higher the opponent’s points, the higher its chance of winning.
Therefore, the best move is square 3 🎉 with the maximum score of 0 for the opponent (minimising player). This position results in either a win or tie for the UC player. The opponent has no chance of winning.
Making a beatable computer player unbeatable
In theory, the above sounds great but how can it be implemented to create an unbeatable computer player? In all honesty, I found translating the above into code extremely difficult.
There are many examples, blogs and videos demonstrating numerous ways to create an unbeatable computer player using minimax. You can find the resources I found helpful at the bottom of this blog post. In this explanation, I’ll try to explain each part of the function.
Before I begin, here is the Minimax class I created. It contains the find_best_move recursive function, which the unbeatable player will use.
The reason for choose_move
To ensure the instance of the board object being used within the game isn’t modified, a new instance of the board is created using the copy_board method. You can see the Board class here.
The purpose of find_best_move’s parameters
def find_best_move(board, depth=0, current_player, opponent)
board is needed in order to:
get all of the squares, consisting of unavailable (taken) and available squares on the board
check if a player has a winning line on the board, or if the board is full (tie)
reset the square was modified, with a player’s mark
depth:
- to keep a track of how many times the recursive function was called
current_player:
- the mark of the player whose turn it is to play a move
opponent:
- the current_player's opponent
best_score and available_squares
best_score = {}
available_squares = board.available_squares
best_score:
- to keep track of the scores for positions
- When all of the available squares have been evaluated, best_score will contain the scores, with the available square as the key. For example:
{3=>-8, 9=>0}
available_squares:
- contains the available squares on the current board as an array
The base case for find_best_move
As mentioned previously, in a recursive function, there should be a base case, which will stop the function if it is triggered. Here it is:
return score_move(board, depth, current_player, opponent) if
board.stop_playing?(current_player, opponent)
If the game is a tie, or either player has won, the game is over. As a result, the recursion should stop. board.stop_playing? returns true if this is the case.
The outcome of playing the initial square should then be scored and returned, to be added to the best_score hash.
A separate method score_move returns the score depending on the outcome.
def score_move(board, depth, current_player, opponent)
if board.winning_line?(current_player)
10 - depth
elsif board.winning_line?(opponent)
depth - 10
elsif board.complete?
0
end
end
Recursive case: Iterating through the available squares
Iterate through the available squares on the board
Play the
current_player’s mark in the selected squareIn the
best_scorehash, set the key as the square, and the value to the outcome score.This is where the recursive function is called again, with slight variation.
boardnow has a mark in a previously available space,depthhas increased by 1. Thecurrent_playerandopponentswitch.board.reset_squareremoves the mark from the available square
Why is the return value of the recursive function multiplied by-1? 🤷🏽♀️
This is something I’m yet to grasp, but here’s a quote from a blog post, explaining the reason:
“Multiplying the return value by -1 will ensure you get either [a positive or negative score] depending on who is last to move.If the game is won on any odd move (1,3,5,7,9), the result will be [positive], which means the current player has won the game.If the game is won on any even move (2,4,6,8), the score will be [negative], which means the opponent would have won the game.”
Recursive case: Evaluating the move
evaluate_move(depth, best_score)
The last part of the find_best_move function is to evaluate the move. My understanding is if the depth is not zero, meaning the recursive function has not returned to the first function call, then return the score.
If the depth is zero, the best move is to be returned as the UC’s player’s move.
def max_best_move(scores)
scores.max_by { |key, value| value }[0]
end
def max_best_score(scores)
scores.max_by { |key, value| value }[1]
end
def evaluate_move(depth, scores)
depth.zero? ? max_best_move(scores) : max_best_score(scores)
end
For example, position 9 was played and the score for the outcome was 0 (a tie). If depth = 1 the score needs to be returned. Remember the best_score hash that’s in the initial recursive function at depth 0? Currently it looks like this:
best_score = {3=-8, 9=> }
It needs the value (0) to match the key (9), to complete the hash. As a result of calling evaluate_move, the score will be returned, and the best_move hash becomes:
best_score = {3=-8, 9=>0}
When depth = 0, the values (scores) of each key (available square) in the hash can be evaluated with evaluate_move. The key with the highest value is returned. In this example, the best move is 9.
In conclusion, this is my understanding of recursion, and using minimax to date. There are still some elements I am unsure about. As my understanding of minimax improves, the way the unbeatable player has been created is likely to change.
You can find the repository for my version of Tic Tac Toe, in Ruby here: https://github.com/ellehallal/ruby-tic-tac-toe






Top comments (0)