SPOILER ALERT
This is a post with my solutions and learnings from the puzzle. Don't continue reading if you haven't tried the puzzle on your own yet.
If you want to do the puzzle, visit adventofcode.com.
TOC
Key learnings
- For-loops
- If statements
You need to understand loops and if-statements to solve the puzzle. You can make it more advanced by optimizing the solution, then there are some more key learnings. Though the input is small enough that no optimization is needed.
Puzzle part 1
You get a list of numbers and the puzzle is: Find the two entries that sum to 2020; what do you get if you multiply them together?.
Input example
The input is a file with numbers. They are in the format of one number per line.
1721
979
366
299
675
1456
Parse input
Start by preparing how to parse the data. My programming language of choice is python:
# Open the input file
inputfile = open('01.input', 'r')
# Parse lines to array of numbers
lines = inputfile.readlines()
entries = [int(x.strip()) for x in lines]
Solution - O(N^2)
A first assumption is made that 1010 isn't on the entry-list. Therefore it doesn't matter if we happen to compare a entry to itself. Otherwise it would give a false positive.
The naive solution is a double for-loop where we check all possible combinations of two entries. For those entries we check if they sum up to 2020, if so it returns the multiplication of them.
In worst case it requires O(N^2). The input-file is 200 lines long, which means 200 * 200 = 40 000 comparisons. It executes within a few seconds on my computer.
def part1(entries):
for x in entries:
for y in entries:
if x + y == 2020:
return x * y
result = part1(entries)
print("Result part 1: %d" % result)
Solution advanced - O(N)
If we use a set to store the rests we can optimize the solution to O(N) in time complexity. The rest is the difference between our current entry X and 2020
X + rest = 2020 ==> rest = 2020 - X
For each entry X we check if we have a value in the rests-set which fulfills X + rest == 2020. Otherwise we store X as a rest.
def part1(entries):
rests = set()
for x in entries:
rest = 2020 - x
if rest in rests:
return rest * x
else:
rests.add(x)
Part 2
The second part of the puzzle is: what is the product of the three entries that sum to 2020?
Solution - O(N^3)
A naive solution is just to add another for loop. This gives us 3 for-loops that in worst case gives time complexity of O(N^3)
def part2(entries):
for x in entries:
for y in entries:
for z in entries:
if x + y + z == 2020:
return x * y * z
Solution - O(N^2)
A more optimized solution is to calculate this in two steps. First using a dictionary to store each possible combination of two entries. This takes O(N^2) time. Then we iterate through the list once again to find the third entry required to meet 2020.
The dictionary has the sum of two entries as key, and multiplication of them as the value.
This solution has time complexity of O(N^2 + N) which is simplified to O(N^2)
def part2(entries):
rests = {}
for x in entries:
for y in entries:
rests[x + y] = x * y
for x in entries:
rest = 2020 - x
if rest in rests:
return x * rests[rest]
Please share if you know a faster way of solving this problem!
Other tricks
Another way to increase performance is to never look at a combination twice. Not sure which time complexity it gives. At least better than O(N^2) and O(N^3) for part 1 and part 2 respectively. Please comment below if you know!
def part1(entries):
size = len(entries)
for i in range(size):
for j in range(i + 1, size):
if entries[i] + entries[j] == 2020:
return entries[i] * entries[j]
def part2(entries):
size = len(entries)
for i in range(size):
for j in range(i + 1, size):
for k in range(j + 1, size):
if entries[i] + entries[j] + entries[k] == 2020:
return entries[i] * entries[j] * entries[k]
Functional style
Some entertainment for the ones that prefer a more functional style of coding. The solutions generates all pairs that sum up to 2020, and then filters on which pair that is present in the list.
def part1functional(arr):
return [
a * b
for (a,b)
in filter(
lambda (a,b): a in arr and b in arr,
zip(range(0, 1010, 1), range(2020, 1010, -1))
)
][0]


Top comments (4)
Thank you for your solutions! I like your solution to part 1 especially, I implemented it first with brute force but then ended up optimizing it, but I still only got O(n log n) performance with sorting the list and then performing binary search. Your solution is a bit simpler and more elegant 😄
For your question about optimizing by never looking into any combination twice, I think it's still
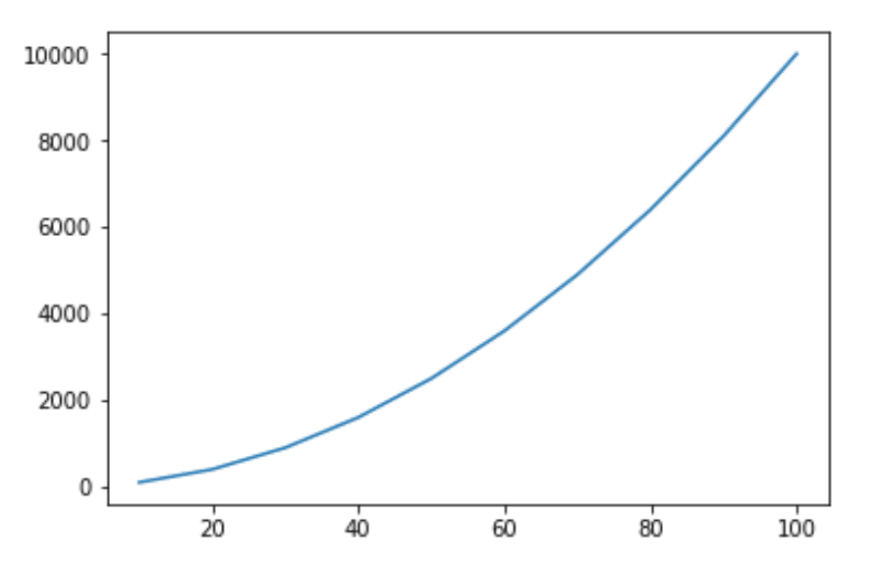
O(n^2)because although in practice we go through less elements, the amount of iterations still increases fast when n increases.So if we have a list of five numbers we have to iterate 4+3+2+1 elements (10 in total). With 10 elements there are 45 iterations, with 20 there are 190 and so on. With 200 elements it's already 19 900 iterations. This can also be expressed as arithmetic sequence: 1+2+3+4+...+n. I had the intuition that the optimization like that doesn't matter, but I couldn't convince myself at first so I draw two plots with python.
This is a picture of growth without the optimization:
This is a picture of growth with the optimization:
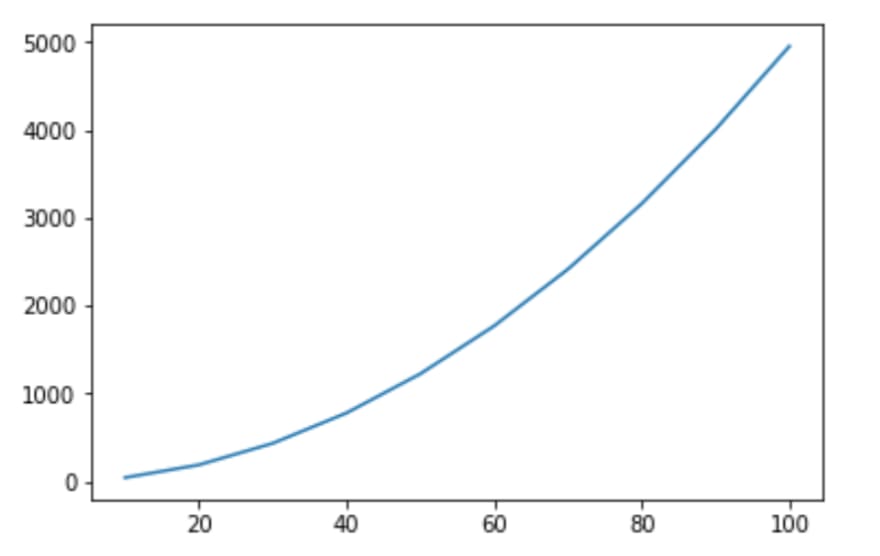
As you can see, the growth is still as fast. I wanted to have some kind of formal proof for that as well, so that's when I googled it and found this stack overflow question and answer: stackoverflow.com/a/44255732 😊
This is of course the case for the part 1 only, I didn't have time to think through how the optimization affects the performance of part 2!
Thanks Anniina for your comment! Great with the visuals and the stack-overflow link. My key take-away is then that the extra keystrokes required to implementing "never check same twice" is not worth haha :)
Oh nice with using sorting and binary search! Seems that python's built-in sort uses timsort which has worst case O(n log(n)). So that would be easy for me to add. How did you solve the binary search part in this puzzle? :)
Haha yeah well in practice it's faster, but the time complexity is still the same.
I just wrote a blog post about different solutions to the puzzle and their time complexities, you can check my sort + binary search solution from the post if you like: dev.to/annisalli/understanding-tim... 😊 The sort + binary sort is still less optimal than your solution with set, but it was fun to implement it!
Nice! Some extra optimisations:
These won't improve the time complexity, but they'll definitely save some time.
I like your solutions. My solution to Part 2 was probably faster but uglier—an outer loop where I added the current number to a set of the numbers we'd seen and an inner loop where I looped over all the numbers we'd seen and checked if the remaining number to get 2020 was also there. But I prefer your approach of computing the sum and product.
I think, in your solution, you could probably combine the second iteration with the first double iteration, since you're iterating over the same set of numbers. Possibly something like: