How to use a DAG to find the longest chain
1. Introduction
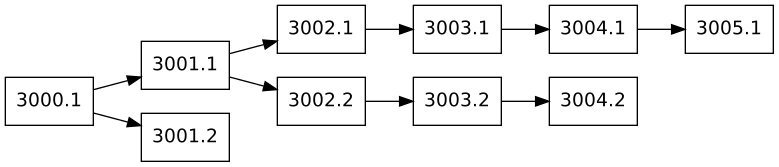
In the first part #1 we talked about how probabilistic finality works and why it's needed. Also we saw an example of how blocks might be structured and linked to each other:
The data structure above resembles a Directed Acyclic Graph (DAG) and fortunately DAGs allow for an easy way to find the longest chain. This is an important part of achieving probabilistic finality.
A DAG is made up of nodes (also called vertices) and edges. An edge represents a link between 2 vertices (e.g. 3000.1->3001.1). We can and should traverse a DAG to find out more about its structure, like how far away is vertex 3005.1 from vertex 3000.1
Additionally a DAG has some unique properties. Find out more about it here
2. How to find the longest chain
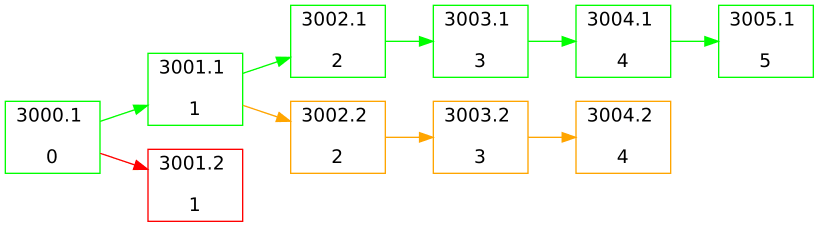
If we look again at the example above, it becomes apparent that 3005.1 is the tip of the longest chain. But how can we find it out programmatically?
We are going to use Depth First Search to traverse the graph and mark every vertex with its distance from the starting vertex.
We start at 3000.1 and give it a distance of 0. Now we traverse through all vertices and give each a distance of parent distance + 1. So 3001.1 has a parent distance of 0 and +1 gives a distance of 1.
3. Conclusion
If we store blocks as a DAG, we can use Depth First Search to find the longest chain.
4. Next Up
We will finally make our hands dirty and implement a DAG in Crystal
UPDATE: #3 Finding the longest chain implementation


Top comments (0)