We are done with the basic sorting algorithms! Bubble Sort, Selection Sort and Insertion Sort were (I hope) easy to understand and wrap your head around. Implementing them will come naturally with time. Truth be told, those basic algorithms have their drawbacks - they do not scale well!
Doubling the size of the input will double the time to produce the sorted array!
Thus, we will move to some more advanced algorithms, whose sorting time will be O(nlog(n)). Without further ado let us introduce the first of those efficient Javascript Sorting algorithms - Merge Sort.
Introduction to Merge Sort
Merge Sort is quite different compared to the sorting algorithms we've seen. Merge sort divides the starting array into smaller arrays of 0 or 1 elements and then merges them back together. No need to loop through the array two times!
The whole process has two major steps:
- Dividing the array
- Merging the smaller arrays back together
Visualization
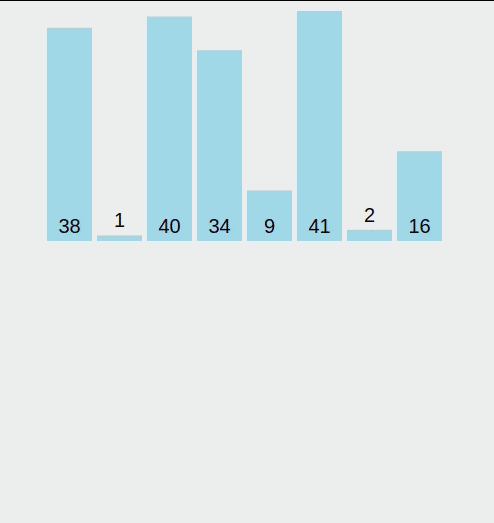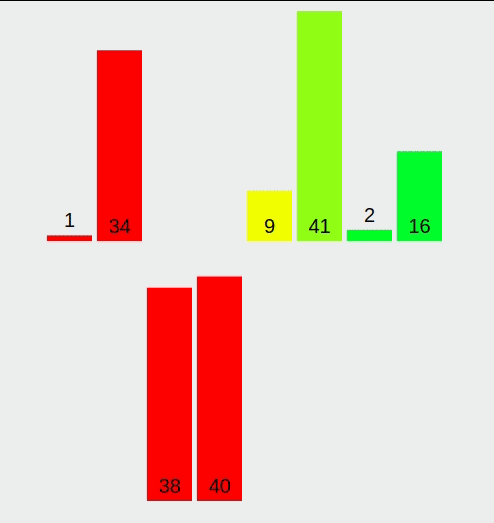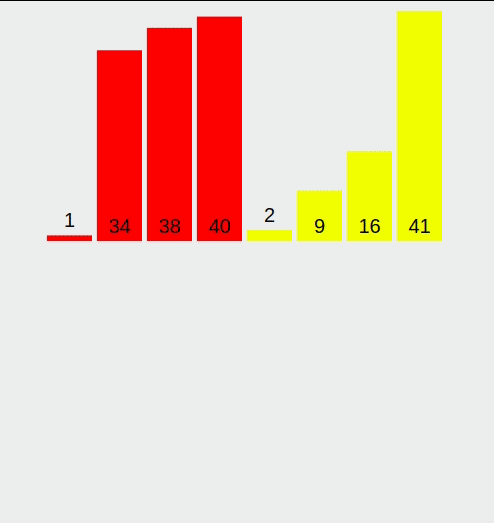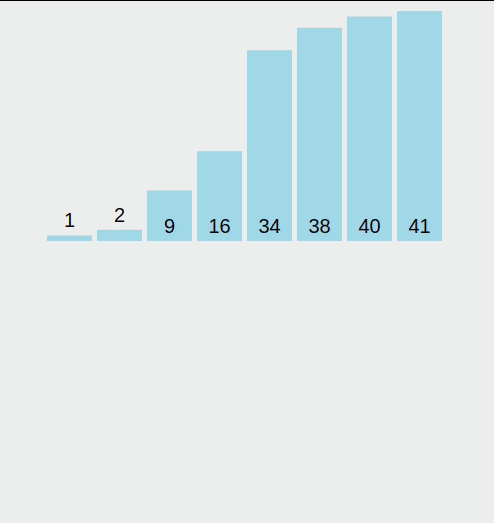
The Inputs for this algorithm are: [38, 1, 40, 34, 9, 41, 2, 16]. 📊
Seems like quite a lot of work right? But it is not, are just dividing the array (colored elements) and then merging the elements back together. Let us first understand the merging logic. At one point in the algorithm we had to merge the following subarrays - [[1, 38], [34, 40]]. Both of those are sorted - which is a requirement in order to produce a new sorted array that will contain all the elements found in those two subarrays.
Merge Implementation
This is the pseudocode for merge sort:
- Create an empty array and create indices i and j
- While there are still values that we haven't looked at1. If the value in the first array is smaller than the value in the second array, we will push that value onto our empty array, increase the value of i, and move on to the next value in the first array2. Otherwise, if the value in the second array is smaller than the value in the first array, we will push that value onto our empty array, increse the value of j, and move on to the next value in the second array
- When all elements from one array are pushed to the sorted array, we will push all the remaining elements from the second array to the sorted array too
function merge(arr1, arr2) {
let results = [];
let i = 0;
let j = 0;
while (i < arr1.length && j < arr2.length) {
if (arr1[i] <= arr2[j]) {
results.push(arr1[i]);
i++;
} else {
results.push(arr2[j]);
j++;
}
}
while (i < arr1.length) {
results.push(arr1[i]);
i++;
}
while (j < arr2.length) {
results.push(arr2[j]);
j++;
}
console.log(results);
return results;
}
Let us go through the code to see what is happening here, taking inputs [[1, 38], [34, 40]] as an example. We have created our empty array and our two indices before running the loop. The loop checks for the values of our indices i and j and whether they are less than the lengths of the two arrays we want to merge. If the element at the index i of arr1 is smaller than the element of the index j of arr2 we push that element onto our results array.
Taking into account our exemplary array we compare values at indices 0 and 0, which are 1 and 34, so we push 1 to the results array and increase the value of i. The next iteration we compare indices at 1 and 0, which are now 38 and 34, and considering 34 is smaller than 38 we push 34 to the results array (which is now [1, 34]), and we increase the value of j. We keep repeating this until we have the finished array, which will be sorted in the end.
Merge Sort Implementation
Keep in mind: this solution uses recursion. Programmers who never worked with recursive code before might find recursion unintuitive, and it might be a good idea to check the link to understand the concept more.
Pseudocode for merge sort is as following:
- The algorithm will continue halving the array until it produces arrays containing no elements or only one element
- Once those arrays exist the algorithm will merge back those arrays (using the method above) until the 'merged' array has the same length as the starting array
function mergeSort(arr) {
if (arr.length <= 1) {
return arr;
} else {
let mid = Math.floor(arr.length / 2);
let left = mergeSort(arr.slice(0, mid));
let right = mergeSort(arr.slice(mid));
return merge(left, right);
}
}
The base says that as soon as the length of the array is one or zero, we return the array, otherwise, we crate the middle element, and then divide the array into two subarrays left, and right, in the end, we call merge on those two arrays.
Now we look back at the visualization.
Conveniently, we have 8 elements in our array. The algorithm first divides the array into 4, then into 2, and then into one element sub-arrays. At one point the elements are all different colors - it means that they are individual. The algorithm then starts merging the elements back together - 38 and 1 become [1, 38], 40 and 34 become [34, 40], and then these two arrays are combined-merged, and the algorithm runs until all the elements are sorted.
Big O Complexity
The best case, average case, and worst case of Merge sort are all the same - O(nlog(n)). Log(n) comes from the number of divisions the algorithm has to make. Having 8 elements means we would need to halve the array three times.
- First time we would get two arrays with 4 elements each
- Second time we would get four arrays with 2 elements each
- Third time we would get eight arrays with one element each
If we would double the size of the input array, we would need to add one division to the algorithm! The n in the formula comes from the number of comparisons done when the arrays are merged back together.
Conclusion
And that is our fourth JavaScript Sorting Algorithm article, with Merge Sort! A tiny bit more comprehensive than the basic three, but still pretty easy to understand, right?! If you liked this one please check the whole series or visit my blog for more tech articles.



Top comments (0)