The Game of Life is not a game in the conventional sense. There are no players, and no winning or losing but its a good coding challenge to solve :)
The universe of the Game of Life is an infinite twodimensional orthogonal grid of square cells, each of which is in one of two possible states, alive or dead. Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent.
Rules:
At each step in time, the following transitions occur:
- Any live cell with fewer than two live neighbours dies as if caused by underpopulation.
- Any live cell with two or three live neighbours lives on to the next generation.
- Any live cell with more than three live neighbours dies, as if by overcrowding.
- Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction. The Game of Life can be simulated using multiple patterns, I have set the default pattern as Glider Pattern (more info can be found here https://en.wikipedia.org/wiki/Glider_(Conway%27s_Life)) but it can be modified to any pattern before starting the game.
I have tried to solve this challenge with the backend using Spring Boot and the front end using React
As seen in the above diagram, the user needs to input data to start the game
- User can modify the dimension of the matrix ( by default 20*20 )
- User can modify the initial generation of live cells (by default glider pattern will be created at the top of the matrix)
- Click START
Solution:
Based on the input data selected, the front end makes a request to the backend to retrieve the next generation of live cells which is populated in the UI.
If the validations are successful (matrix dimension is valid), in order to generate the next set of generations below steps are performed.
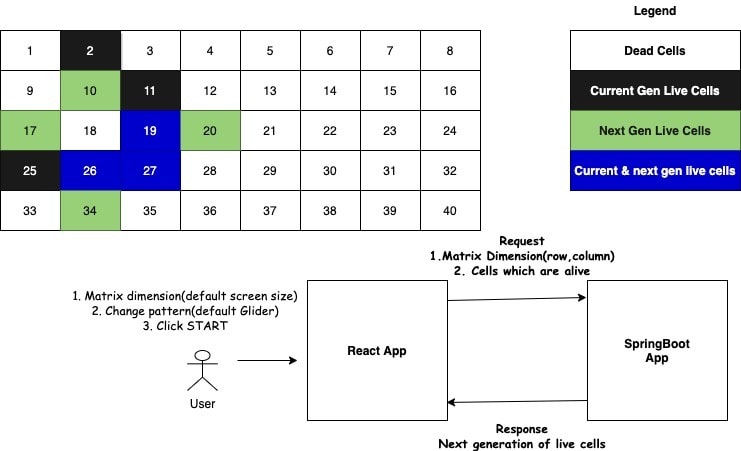
Consider eg an 8 * 5 dimension with initial live cells as [10, 19, 25, 26, 27]
- For each of the initial generation, identify its nearest unique neighbours considering border conditions. In the above diagram example, [1, 3, 6, 7, 8, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]
It's best to use a HashSet in this case as this data further will be used for searching and searching in a HashSet will result in O(1)
- For each of the identified cells, check whether they are going to be alive in the next generation by applying rules by identifying the neighbour for each cell and count the number of cells which are ALIVE in the current generation (by comparing against input).
For eg, Cell 1 (current dead cell) -> neighbours are 2(L), 9, 10 and only one cell is currently live and hence as per rules, it won't survive the next generation.
Also for cell 10(current dead cell), -> neighbours are 1, 2(L), 3, 9, 11(L), 17, 18, 19(L) and exactly 3 cells are currently live which will make 10 to be alive in next generation
Also for cell 19( current live cell), -> neighbours are 10, 11(L), 12, 18, 20, 26(L), 27(L), 28. We will have 3 cells that are currently live and as per rules, this can survive in the next generation.
Similarly for each cell, their next-generation status is identified.
- Collect the cells which are alive in the next generation and return the result set
This solution is available in Game of Life UI
Regardless of the size of the matrix, this solution would take constant time(considering a finite number of alive cells) because the size of the matrix is not used in any calculation apart from identifying the neighbour cells which will be constant. If you have solved this problem in a more efficient approach, Please share it here I would like to know.







Top comments (0)