Linear Algebra
Linear algebra is the branch of mathematics that deals with vector spaces. It contains concept of vector, matrix etc. Linear algebra is widely used by data scientists (frequently implicitly, and not infrequently by people who don’t understand it). It wouldn’t be a bad idea to read a textbook.
Vector
Vectors, in general, are objects that can be added together (to form new vectors) and that can be multiplied by scalars (numbers) to create new vectors Vectors are concretely (for us) points in some finite-dimensional space. Although you may not think of your data as vectors, they are a good way to represent numerical data. For instance, if you have a large number of people's heights, weights, and ages, You can think of your data as three-dimensional vectors (height, weight, age). If If you're teaching a class with four exams, you can treat student grades as four-point scale. vectors with dimensions (exam1, exam2, exam3, exam4). The most basic method is to represent vectors as lists of numbers. A list of three numbers corresponds to a vector in three-dimensional space, and vice versa:
weight = [
10, # kg
20, # kg
30 # Kg
]
length = [
15, # meter
25 # Meter
]
One issue with this approach is that we will want to perform arithmetic on vectors. Because Python lists aren't vectors (and thus don't support vector operations), arithmetic), we'll have to create our own arithmetic tools. So let's start there. To begin, we'll frequently need to combine two vectors. Vectors are added component by component. This means that if two vectors v and w have the same length, their sum is the vector itself. whose first element is , second element is , and so on on. (If they're not the same length, we can't combine them.)
Adding and will result in .
We can easily implement this by zip-ing the vectors together and using a list comprehension to add the corresponding elements:
def vector_add(v, w):
"""adds corresponding elements"""
return [v_i + w_i
for v_i, w_i in zip(v, w)]
Similarly, to subtract two vectors we just subtract corresponding elements:
def vector_subtract(v, w):
"""subtracts corresponding elements"""
return [v_i - w_i
for v_i, w_i in zip(v, w)]
We’ll also need to be able to multiply a vector by a scalar, which we do simply by multiplying each element of the vector by that number:
def scalar_multiply(c, v):
"""c is a number, v is a vector"""
return [c * v_i for v_i in v]
We also need dot product of two vectors. The dot product of two vectors is the sum of their component wise product:
def dot(v, w):
return sum(v_i * w_i for v_i, w_i in zip(v, w))
Another value which can be useful is the Magnitude (or length) of the vector which is square root of sum of square of values.
Distance between two vectors can be calculated by
import math
def sum_of_squares(v):
"""v_1 * v_1 + ... + v_n * v_n"""
return dot(v, v)
def magnitude(v):
return math.sqrt(sum_of_squares(v))
def squared_distance(v, w):
"""(v_1 - w_1) ** 2 + ... + (v_n - w_n) ** 2"""
return sum_of_squares(vector_subtract(v, w))
def distance(v, w):
return math.sqrt(squared_distance(v, w))
Matrices
A matrix is a two-dimensional number collection. Matrixes will be represented as lists of lists, with each inner list the same size and representing a row of the matrix. If A is a matrix, then is the element in the ith row and the jth column. Per mathematical convention, we will typically use capital letters to represent matrices.
Same as vectors we can represent matrix in terms of 2D list.
A = [
[1,2,3],
[4,5,6]
]
The matrix A contains len(A) rows and len(A[0]) columns, which we take to be its shape given this list-of-lists representation:
def shape(A):
n_rows = len(A)
n_columns = len(A[0])
return n_rows, n_columns
We shall refer to a matrix as a
matrix if it contains n rows and k columns. Each row of a n by k matrix can be thought of as a vector of length k, and each column as a vector of length n:
def get_row(A, i):
return A[i] # A[i] is already the ith row
def get_column(A, j):
return [A_i[j] # jth element of row A_i
for A_i in A] # for each row A_i
If a diagonal of a matrix contains only 1s then its called Diagonal Matrix.
We can use matrix to represent relations between different entities ex:
friendships = [(0, 1), (0, 2), (1, 2), (1, 3), (2, 3), (3, 4), (4, 5), (5, 6), (5, 7), (6, 8), (7, 8), (8, 9)]
############# Which Can Also be Represnted as ###############
friendships = [ [0, 1, 1, 0, 0, 0, 0, 0, 0, 0], # user 0
[1, 0, 1, 1, 0, 0, 0, 0, 0, 0], # user 1
[1, 1, 0, 1, 0, 0, 0, 0, 0, 0], # user 2
[0, 1, 1, 0, 1, 0, 0, 0, 0, 0], # user 3
[0, 0, 0, 1, 0, 1, 0, 0, 0, 0], # user 4
[0, 0, 0, 0, 1, 0, 1, 1, 0, 0], # user 5
[0, 0, 0, 0, 0, 1, 0, 0, 1, 0], # user 6
[0, 0, 0, 0, 0, 1, 0, 0, 1, 0], # user 7
[0, 0, 0, 0, 0, 0, 1, 1, 0, 1], # user 8
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0]] # user 9
If there are very few connections, this is a much more inefficient representation, since you end up having to store a lot of zeroes. However, with the matrix representation it is much quicker to check whether two nodes are connected, you just have to do a matrix lookup instead of (potentially) inspecting every edge:
friendships[0][2] == 1 # True, 0 and 2 are friends
friendships[0][8] == 1 # False, 0 and 8 are not friends
friends_of_five = [i # only need
for i, is_friend in enumerate(friendships[5]) # to look at
if is_friend] # one row
Resource
- https://www.khanacademy.org/math/linear-algebra
- https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
- https://web.stanford.edu/~boyd/vmls/
- http://mitran-lab.amath.unc.edu/courses/MATH347DS/textbook.pdf
- https://fong.cs.wmich.edu/modules/LinearAlgebraPrimerConcepts.pdf
References
This article is highly influenced by the book Data Science from Scratch by Joel Grus, this is a fantastic book to read for people getting started with data science. If you don't like reading book then save the series as there is more to come.


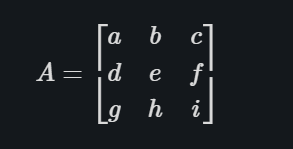




Top comments (0)
Some comments may only be visible to logged-in visitors. Sign in to view all comments.