A quick introduction to the topic of fairness with hands on coding. Evaluate your machine learning model fairness in just a few lines of code.
Photo by Wesley Tingey on Unsplash
Are Machine Learning models "fair"? When increasingly more decisions are backed by ML algorithms, it becomes important to understand the biases they can create.
But what does "fairness" mean? This is where it gets a little political (and mathematical)… To illustrate our thoughts, we'll take the example of a machine learning model which predicts whether a salary should be higher than 50K/year based on a number of features including age and gender.
And maybe you've already guessed, by looking at these two features, that fairness can have different definitions. Fair for gender might mean that we want to have the a prediction which is independent of gender (i.e. paying the same people who only differ by their gender). Fair for age might mean something else. We'd probably want to allow a certain correlation between the prediction and the age, as it seems fair to pay better older individuals (which usually are more experienced).
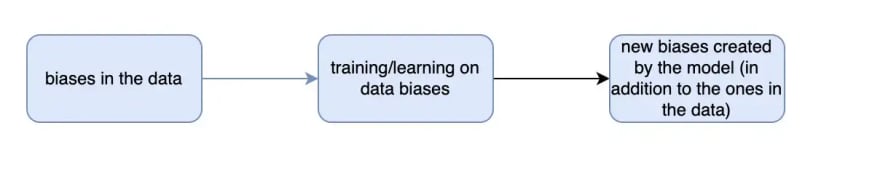
One key thing to understand is that what is judged "fair" is sometimes not even respected in the data itself.
How would the model learn that men and women should be paid the same at equal levels it it does not observe this in the data itself ?
Figure1: data biases vs model biases
Now that we have a bit of context on the problem, let's get into the math (Section 1) and the code (Sections 2 and 3)to be able to evaluate and address unfairness issues:
- A few fairness concepts
- Evaluating Data Biases
-
Evaluating and Correcting Model Biases with Fairlearn
a. Evaluating bias
b. Correcting bias
All the code for this tutorial can be found on Kaggle here. Feel free to run the notebook yourself or create a copy!
1. A few fairness concepts
1.1. Mathematical definition of fairness
In order to simplify things, we'll restrict the scope to binary classification (predict whether someone should be paid more than 50K/year).
Usually, we'll call:
- X: the feature matrix
- Y: the target
- A: Sensitive feature, usually one of the columns of X
For binary classification, two main definition of fairness exist:
-
Demographic parity (also known as statistical parity): A classifier h satisfies demographic parity under a distribution over (X,A,Y) if its prediction h(X) is statistically independent of the sensitive feature A. This is equivalent to:
E[h(X)|A=a]=E[h(X)] -
Equalized odds: A classifier h satisfies equalized odds under a distribution over (X,A,Y) if its prediction h(X) is conditionally independent of the sensitive feature A given the label Y. This is equivalent to:
E[h(X)|A=a,Y=y]=E[h(X)|Y=y]
NOTE: a third one exists but is more rarely used: equal opportunity is a relaxed version of equalized odds that only considers conditional expectations with respect to positive labels.
1.2. Fairness in words
In "simpler words":
- Demographic parity: the prediction should be independent from the sensitive features (for instance independent from gender). It states that all categories from the protected feature should receive the positive outcome at the same rate (it plays on selection rate)
- Equalized odds: the prediction can be correlated to the sensitive feature, to the extent it is explained by the data we see
1.3. Why does it matter?
OK, that's interesting, but why does it matter? And how can I use those mathematical concepts?
→ Let's take two examples of features and then explain what type of fairness we want to have for this feature. Going back to the previous example of salary prediction, let's say you are the CEO of a very big company and want to build an algorithm which would give you the salary you should give to your employees based on performance indicators. Ideally you would look for something like:
- Demographic Parity for gender: the salary prediction should be independent from the gender
- Equalized Odds for Age: the salary prediction should not be independent from Age (you want to still pay more employees with more experience) but you still want to control that the salary so that you do not end up being too skewed → you don't want to end up in the situation where the algorithm exacerbates even more the inequalities (pays the youth even less and the elders even more)
Without further due, let's get into the implementation details on how we can evaluate fairness and "retrain" our Machine Learning models against its biases. For this we're going to use the UCI Adult Dataset.
2. Evaluating Data Biases
NOTE: once again, you can find all the associated code here.
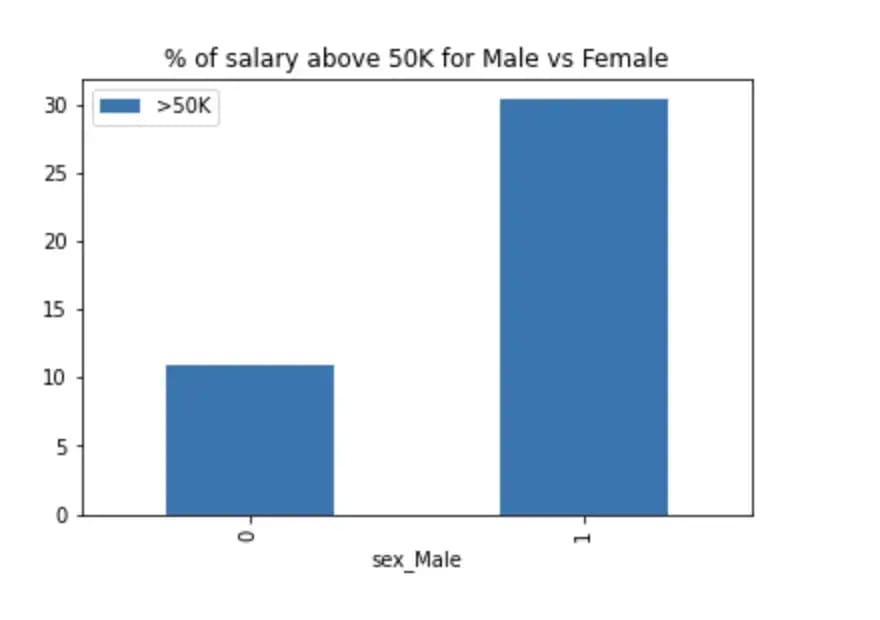
Biases can exist in the data itself. Let's just load the data and plot the percentage of Male/Female having a salary above 50K.
Figure 2: gender and age impact on salary
We see that the percentage of males having a salary above 50K is almost 3x the percentage of females. (!!)
If the algorithm learns on this data it will definitely be biased. To counter this bias we can either:
- cherry pick data so that the percentage of male
- use fairlearn to correct the bias after the model is trained on this unfair data
In section 3, we'll focus on the second approach.
3. Evaluating and Correcting Model Biases with Fairlearn
3.1. Evaluating bias
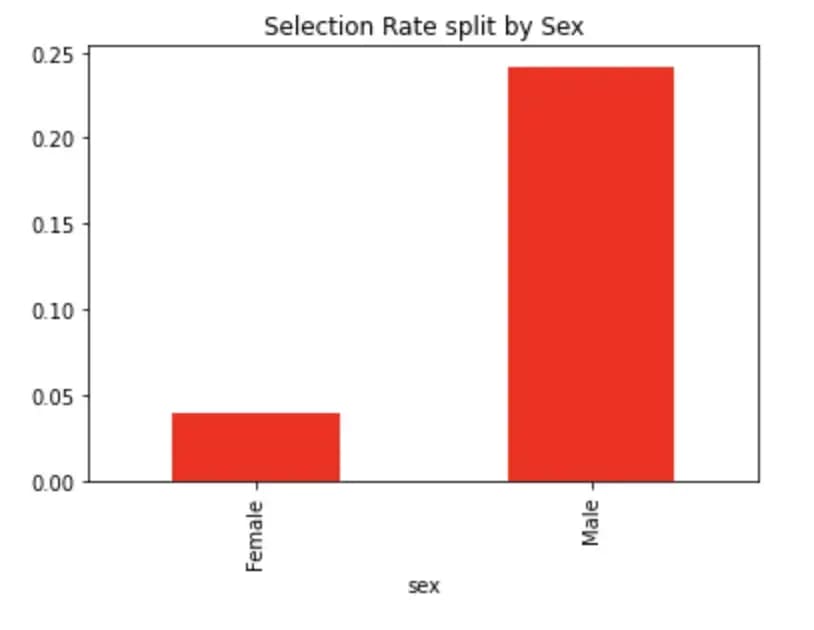
One of the most interesting features here is probably selection rate. It is the rate of predicting positive outcomes (in this case, whether salary is above 50K)
Figure 3: Selection Rate Definition
Let's use MetricFrame from fairlearn to calculate the selection rates split by Sex.
from fairlearn.metrics import MetricFrame
from sklearn.metrics import accuracy_score,precision_score,recall_score
from sklearn.ensemble import GradientBoostingClassifier
from fairlearn.metrics import selection_rate
from fairlearn.reductions import ExponentiatedGradient, DemographicParity
classifier = GradientBoostingClassifier()
classifier.fit(X, y)
y_pred = classifier.predict(X)
metrics = {
'accuracy': accuracy_score,
'precision': precision_score,
'recall': recall_score,
'selection_rate': selection_rate
}
metric_frame = MetricFrame(metrics=metrics,
y_true=y,
y_pred=y_pred,
sensitive_features=sex)
metric_frame.by_group['selection_rate'].plot.bar(color= 'r', title='Selection Rate split by Sex')
Figure 4: Selection Rate Split by Sex
We see that the percentage of males having a salary above 50K is almost 3x the percentage of females. (!!)
Once the model is trained we see that this ratio is now 5x (!!). The model is exacerbating the bias we see in the data.
3.2. Correcting bias
Let's now correct the bias we observe by applying Demographic Parity on our classifier (we use ExponentiatedGradient from fairlearn for this). More context on how it works behind the scene can be found on the official fairlearn documentation here.
np.random.seed(0) # set seed for consistent results with ExponentiatedGradient
constraint = DemographicParity()
classifier = GradientBoostingClassifier()
mitigator = ExponentiatedGradient(classifier, constraint)
mitigator.fit(X, y, sensitive_features=sex)
y_pred_mitigated = mitigator.predict(X)
sr_mitigated = MetricFrame(metrics=selection_rate, y_true=y, y_pred=y_pred_mitigated, sensitive_features=sex)
print(sr_mitigated.overall)
print(sr_mitigated.by_group)
metric_frame_mitigated = MetricFrame(metrics=metrics,
y_true=y,
y_pred=y_pred_mitigated,
sensitive_features=sex)
metric_frame_mitigated.by_group.plot.bar(
subplots=True,
layout=[3, 3],
legend=False,
figsize=[12, 8],
title="Show all metrics",
)
Figure 5: Selection rate for original model vs mitigated one
By mitigating the model we introduced demographic parity (and thus equal selection rates) for our new model. Our model is now fair!!!
Woohoo! You now know the basics of fairness works and how you can start using it right away in your machine learning projects!
I hope you liked this article! Let me know if you have any questions or suggestions. Also feel free to contact me on LinkedIn, GitHub or Twitter, or checkout some other articles I wrote on DS/ML best practices. Happy learning!
Sources:
About me
Hey! 👋 I'm Armand Sauzay (armandsauzay). You can find, follow or contact me on:





Top comments (0)