32 Linked List Interview Questions (ANSWERED) To Nail Your Coding Interview

Linked lists are among the simplest and most common data structures. They can be used to implement several other common abstract data types, including lists, stacks, queues, associative arrays and etc. Follow along and check 43 most common Linked List Interview Questions with Answers and Solutions to stay prepare for your next coding interview.

Originally published on FullStack.Cafe - Kill Your Next Tech Interview

Q1: Name some advantages of Linked List ☆

Topics: Linked Lists

Answer:

There are some:

• Linked Lists are Dynamic Data Structure - it can grow and shrink at runtime by allocating and deallocating memory. So there is no need to give initial size of linked list.
• Insertion and Deletion are simple to implement - Unlike array here we don’t have to shift elements after insertion or deletion of an element. In linked list we just have to update the address present in next pointer of a node.
• Efficient Memory Allocation/No Memory Wastage - In case of array there is lot of memory wastage, like if we declare an array of size 10 and store only 6 elements in it then space of 4 elements are wasted. There is no such problem in linked list as memory is allocated only when required.

🔗 Source: www.thecrazyprogrammer.com

Q2: Convert a Single Linked List to a Double Linked List ☆☆

Topics: Linked Lists

Answer:

A doubly linked list is simply a linked list where every element has both next and prev mebers, pointing at the elements before and after it, not just the one after it in a single linked list.

so to convert your list to a doubly linked list, just change your node to be:

private class Node
{
    Picture data;
    Node pNext;
    Node pPrev;
};

and when iterating the list, on each new node add a reference to the previous node.

🔗 Source: stackoverflow.com

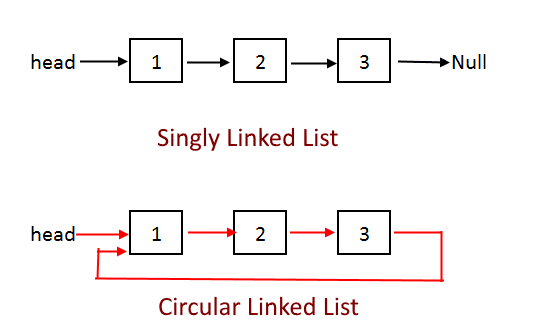
Q3: Convert a Singly Linked List to Circular Linked List ☆☆

Topics: Linked Lists

Answer:

To convert a singly linked list to circular linked list, we will set next pointer of tail node to head pointer.

• Create a copy of head pointer, let's say temp.
• Using a loop, traverse linked list till tail node (last node) using temp pointer.
• Now set the next pointer of tail node to head node. temp\->next = head

Implementation:

PY

def convertTocircular(head):
    # declare a node variable
    # start and assign head
    # node into start node.
    start = head

    # check that
    while head.next
    # not equal to null then head
    # points to next node.
    while(head.next is not None):
      head = head.next

    #
    if head.next points to null
    # then start assign to the
    # head.next node.
    head.next = start
    return start

🔗 Source: www.techcrashcourse.com

Q4: Detect if a List is Cyclic using Hash Table ☆☆

Topics: Linked Lists Hash Tables

Answer:

To detect if a list is cyclic, we can check whether a node had been visited before. A natural way is to use a hash table.

Algorithm

We go through each node one by one and record each node's reference (or memory address) in a hash table. If the current node is null, we have reached the end of the list and it must not be cyclic. If current node’s reference is in the hash table, then return true.

Complexity Analysis:

Time Complexity: O(n)
Space Complexity: O(n)

• Time complexity : O(n) . We visit each of the n elements in the list at most once. Adding a node to the hash table costs only O(1) time.
• Space complexity: O(n) . The space depends on the number of elements added to the hash table, which contains at most n elements. ### Implementation: #### Java

public boolean hasCycle(ListNode head) {
    Set<ListNode> nodesSeen = new HashSet<>();
    while (head != null) {
        if (nodesSeen.contains(head)) {
            return true;
        } else {
            nodesSeen.add(head);
        }
        head = head.next;
    }
    return false;
}

🔗 Source: leetcode.com

Q5: How to reverse a singly Linked List using only two pointers? ☆☆

Topics: Linked Lists

Answer:

Nothing faster than O(n) can be done. You need to traverse the list and alter pointers on every node, so time will be proportional to the number of elements.

Implementation:

Java

public void reverse(Node head) {
    Node curr = head, prev = null;

    while (head.next != null) {
        head = head.next; // move the head to next node
        curr.next = prev; // break the link to the next node and assign it to previous
        prev = curr;      // we are done with previous, move it to next node
        curr = head;      // current moves along with head
    }

    head.next = prev;     //for last node
}

🔗 Source: stackoverflow.com

Q6: Insert an item in a sorted Linked List maintaining order ☆☆

Topics: Sorting Linked Lists

Answer:

The add() method below walks down the list until it finds the appropriate position. Then, it splices in the new node and updates the start, prev, and curr pointers where applicable.

Note that the reverse operation, namely removing elements, doesn't need to change, because you are simply throwing things away which would not change any order in the list.

Implementation:

Java

public void add(T x) {
    Node newNode = new Node();
    newNode.info = x;

    // case: start is null; just assign start to the new node and return
    if (start == null) {
        start = newNode;
        curr = start;
        // prev is null, hence not formally assigned here
        return;
    }

    // case: new node to be inserted comes before the current start;
    //       in this case, point the new node to start, update pointers, and return
    if (x.compareTo(start.info) < 0) {
        newNode.link = start;
        start = newNode;
        curr = start;
        // again we leave prev undefined, as it is null
        return;
    }

    // otherwise walk down the list until reaching either the end of the list
    // or the first position whose element is greater than the node to be
    // inserted; then insert the node and update the pointers
    prev = start;
    curr = start;
    while (curr != null && x.compareTo(curr.info) >= 0) {
        prev = curr;
        curr = curr.link;
    }

    // splice in the new node and update the curr pointer (prev already correct)
    newNode.link = prev.link;
    prev.link = newNode;
    curr = newNode;
}

🔗 Source: stackoverflow.com

Q7: Under what circumstances are Linked Lists useful? ☆☆

Topics: Linked Lists Data Structures

Answer:

Linked lists are very useful when you need :

• to do a lot of insertions and removals, but not too much searching, on a list of arbitrary (unknown at compile-time) length.
• splitting and joining (bidirectionally-linked) lists is very efficient.
• You can also combine linked lists - e.g. tree structures can be implemented as "vertical" linked lists (parent/child relationships) connecting together horizontal linked lists (siblings).

Using an array based list for these purposes has severe limitations:

• Adding a new item means the array must be reallocated (or you must allocate more space than you need to allow for future growth and reduce the number of reallocations)
• Removing items leaves wasted space or requires a reallocation
• inserting items anywhere except the end involves (possibly reallocating and) copying lots of the data up one position

🔗 Source: stackoverflow.com

Q8: What are some types of Linked List? ☆☆

Topics: Linked Lists Data Structures

Answer:

• A singly linked list

• A doubly linked list is a list that has two references, one to the next node and another to previous node.

• A multiply linked list - each node contains two or more link fields, each field being used to connect the same set of data records in a different order of same set(e.g., by name, by department, by date of birth, etc.).
• A circular linked list - where last node of the list points back to the first node (or the head) of the list.

🔗 Source: www.cs.cmu.edu

Q9: What is a cycle/loop in the singly-linked list? ☆☆

Topics: Linked Lists

Answer:

A cycle/loop occurs when a node’s next points back to a previous node in the list. The linked list is no longer linear with a beginning and end—instead, it cycles through a loop of nodes.

🔗 Source: www.interviewcake.com

Q10: What is complexity of push and pop for a Stack implemented using a LinkedList? ☆☆

Topics: Linked Lists Stacks Big-O Notation

Answer:

O(1). Note, you don't have to insert at the end of the list. If you insert at the front of a (singly-linked) list, they are both O(1).

Stack contains 1,2,3:

[1]->[2]->[3]

Push 5:

[5]->[1]->[2]->[3]

Pop:

[1]->[2]->[3] // returning 5

🔗 Source: stackoverflow.com

Q11: What is time complexity of Linked List operations? ☆☆

Topics: Linked Lists

Answer:

• A linked list can typically only be accessed via its head node. From there you can only traverse from node to node until you reach the node you seek. Thus access is O(n).
• Searching for a given value in a linked list similarly requires traversing all the elements until you find that value. Thus search is O(n).
• Inserting into a linked list requires re-pointing the previous node (the node before the insertion point) to the inserted node, and pointing the newly-inserted node to the next node. Thus insertion is O(1).
• Deleting from a linked list requires re-pointing the previous node (the node before the deleted node) to the next node (the node after the deleted node). Thus deletion is O(1).

🔗 Source: github.com

Q12: Split the Linked List into k consecutive linked list "parts" ☆☆☆

Topics: Linked Lists

Problem:

Given a (singly) linked list with head node root, write a function to split the linked list into k consecutive linked list "parts".

• The length of each part should be as equal as possible: no two parts should have a size differing by more than 1. This may lead to some parts being null.
• The parts should be in order of occurrence in the input list, and parts occurring earlier should always have a size greater than or equal parts occurring later.
• Return a List of ListNode's representing the linked list parts that are formed

Example:

[1,2,3,4,5,6,7,8,9,10], k=3
ans = [ [1,2,3,4] [5,6,7] [8,9,10] ]

Solution:

• If there are N nodes in the linked list root, then there are N/k items in each part, plus the first N%k parts have an extra item. We can count N with a simple loop.
• Now for each part, we have calculated how many nodes that part will have: width + (i < remainder ? 1 : 0). We create a new list and write the part to that list.

Implementation:

Java

public ListNode[] splitListToParts(ListNode root, int k) {
  ListNode cur = root;
  int N = 0;
  while (cur != null) {
    cur = cur.next;
    N++;
  }

  int width = N / k, rem = N % k;

  ListNode[] ans = new ListNode[k];
  cur = root;
  for (int i = 0; i < k; ++i) {
    ListNode head = new ListNode(0), write = head;
    for (int j = 0; j < width + (i < rem ? 1 : 0); ++j) {
      write = write.next = new ListNode(cur.val);
      if (cur != null) cur = cur.next;
    }
    ans[i] = head.next;
  }
  return ans;
}

PY

def splitListToParts(self, root, k):
    cur = root
    for N in xrange(1001):
        if not cur: break
        cur = cur.next
    width, remainder = divmod(N, k)

    ans = []
    cur = root
    for i in xrange(k):
        head = write = ListNode(None)
        for j in xrange(width + (i < remainder)):
            write.next = write = ListNode(cur.val)
            if cur: cur = cur.next
        ans.append(head.next)
    return ans

🔗 Source: leetcode.com

Q13: Compare Array based vs Linked List stack implementations ☆☆☆

Topics: Arrays Linked Lists Stacks

Answer:

The following implementations are most common:

• Stack backed by a singly-linked list. Because a singly-linked list supports O(1) time prepend and delete-first, the cost to push or pop into a linked-list-backed stack is also O(1) worst-case. However, each new element added requires a new allocation, and allocations can be expensive compared to other operations. The locality of the linked list is not as good as the locality of the dynamic array since there is no guarantee that the linked list cells will be stored contiguously in memory.

• Stack backed by a dynamic array. Pushing onto the stack can be implemented by appending a new element to the dynamic array, which takes amortised O(1) time and worst-case O(n) time. Popping from the stack can be implemented by just removing the last element, which runs in worst-case O(1) (or amortised O(1) if you want to try to reclaim unused space). In other words, the most common implementation has best-case O(1) push and pop, worst-case O(n) push and O(1) pop, and amortised O(1) push and O(1) pop.

🔗 Source: stackoverflow.com

Q14: Convert a Binary Tree to a Doubly Linked List ☆☆☆

Topics: Binary Tree Divide & Conquer Linked Lists Recursion Data Structures

Answer:

This can be achieved by traversing the tree in the in-order manner that is, left the child -> root ->right node.

In an in-order traversal, first the left sub-tree is traversed, then the root is visited, and finally the right sub-tree is traversed.

One simple way of solving this problem is to start with an empty doubly linked list. While doing the in-order traversal of the binary tree, keep inserting each element output into the doubly linked list. But, if we look at the question carefully, the interviewer wants us to convert the binary tree to a doubly linked list in-place i.e. we should not create new nodes for the doubly linked list.

This problem can be solved recursively using a divide and conquer approach. Below is the algorithm specified.

• Start with the root node and solve left and right sub-trees recursively
• At each step, once left and right sub-trees have been processed:
  • fuse output of left subtree with root to make the intermediate result
  • fuse intermediate result (built in the previous step) with output from the right sub-tree to make the final result of the current recursive call

Complexity Analysis:

Time Complexity: O(n)
Space Complexity: O(n)

Recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of binary tree h. It will be O(log n) for balanced tree and in worst case can be O(n).

Implementation:

Java

public static void BinaryTreeToDLL(Node root) {
    if (root == null)
        return;
    BinaryTreeToDLL(root.left);
    if (prev == null) { // first node in list
        head = root;
    } else {
        prev.right = root;
        root.left = prev;
    }
    prev = root;
    BinaryTreeToDLL(root.right);
    if (prev.right == null) { // last node in list
        head.left = prev;
        prev.right = head;
    }
}

PY

def BinaryTreeToDLL(self, node):    
    #Checks whether node is None    
    if(node == None):    
        return;    

    #Convert left subtree to doubly linked list    
    self.BinaryTreeToDLL(node.left);    

    #If list is empty, add node as head of the list    
    if(self.head == None):    
        #Both head and tail will point to node    
        self.head = self.tail = node;    
    #Otherwise, add node to the end of the list    
    else:    
        #node will be added after tail such that tail's right will point to node    
        self.tail.right = node;    
        #node's left will point to tail    
        node.left = self.tail;    
        #node will become new tail    
        self.tail = node;    

    #Convert right subtree to doubly linked list    
    self.BinaryTreeToDLL(node.right);  

🔗 Source: www.educative.io

Q15: Find similar elements from two Linked Lists and return the result as a Linked List ☆☆☆

Topics: Linked Lists Hash Tables

Problem:

Consider:

list1: 1->2->3->4->4->5->6
list2: 1->3->6->4->2->8

Result:

list3: 1->2->3->4->6

Solution:

1. Create a hash table or set
2. Go through list1, mark entries as you visit them. O(N)
3. Go through list2, mark entries (with different flag) as you visit them. O(M)
4. Traverse hash table and find all the entries with both flags. Create list3 as you find entries. O(H)

Total Complexity: O(N)+ O(M) + O(Max(N,H,M)) => O(N)

Complexity Analysis:

Time Complexity: O(n)

🔗 Source: stackoverflow.com

Q16: Floyd's Cycle Detect Algorithm: Explain how to find a starting node of a Cycle in a Linked List? ☆☆☆

Topics: Linked Lists

Answer:

This is Floyd's algorithm for cycle detection. Once you've found a node that's part of a cycle, how does one find the start of the cycle?

• In the first part of Floyd's algorithm, the hare moves two steps for every step of the tortoise. If the tortoise and hare ever meet, there is a cycle, and the meeting point is part of the cycle, but not necessarily the first node in the cycle.
• Once tortoise and hare meet, let's put tortoise back to the beginning of the list and keep hare where they met (which is k steps away from the cycle beginning). The hypothesis (see math explanation) is that if we let them move at the same speed (1 step for both), the first time they ever meet again will be the cycle beginning.

Another solution to mention is Hash Map:

• Traverse the nodes list.
• For each node encountered, add it to the identity hash map
• If the node already existed in the identity map then the list has a circular link and the node which was prior to this conflict is known (either check before moving or keep the "last node")

Implementation:

Java

public ListNode getLoopStartingPoint(ListNode head) {
    boolean isLoopExists = false;
    ListNode slowPtr = head, fastPtr = head;

    while (!Objects.isNull(fastPtr) && !Objects.isNull(fastPtr.getNext())) {
        slowPtr = slowPtr.getNext();
        fastPtr = fastPtr.getNext().getNext();
        if (slowPtr == fastPtr) {
            isLoopExists = true;
            break;
        }
    }

    if (!isLoopExists) return null;

    slowPtr = head;
    while (slowPtr != fastPtr) {
        slowPtr = slowPtr.getNext();
        fastPtr = fastPtr.getNext();
    }
    return slowPtr;
}

🔗 Source: stackoverflow.com

Q17: Floyd's Cycle Detect Algorithm: Remove Cycle (Loop) from a Linked List ☆☆☆

Topics: Linked Lists

Answer:

1. Floyd's cycle detect algorithm, also called the tortoise and hare algorithm as it involves using two pointers/references that move at different speeds, is one way of detecting the cycle. If there is a cycle, the two pointers (say slow and fast) will end up pointing to the same element after a finite number of steps. Interestingly, it can be proved that the element at which they meet will be the same distance to the start of the **loop* (continuing to traverse the list in the same, forward direction) as the start of the loop is to the head of the list*. That is, if the linear part of the list has k elements, the two pointers will meet inside the loop of length m at a point m-k from the start of the loop or k elements to the 'end' of the loop (of course, it's a loop so it has no 'end' - it's just the 'start' once again). And that gives us a way to find the start of the loop:

2. Once a cycle has been detected, let fast remain pointing to the element where the loop for the step above terminated but reset slow so that it's pointing back to the head of the list. Now, move each pointer one element at a time. Since fast began inside the loop, it will continue looping. After k steps (equal to the distance of the start of the loop from the head of the list), slow and fast will meet again. This will give you a reference to the start of the loop.

3. It is now easy to set slow (or fast) to point to the element starting the loop and traverse the loop until slow ends up pointing back to the starting element. At this point slow is referencing the 'last' element list and it's next pointer can be set to null.

Implementation:

Java

public static LinkedListNode lastNodeOfTheLoop(LinkedListNode head) {
    LinkedListNode slow = head;
    LinkedListNode fast = head; 

    // find meeting point using Tortoise and Hare algorithm
    // this is just Floyd's cycle detection algorithm
    while (fast.next != null) { 
        slow = slow.next; 
        fast = fast.next.next; 
        if (slow == fast) { 
            break; 
        }
    }

    // Error check - there is no meeting point, and therefore no loop
    if (fast.next == null) {
        return null;
    }

    slow = head; 
    // Until both the references are one short of the common element which is the start of the loop
    while (slow.next != fast.next) { 
        slow = slow.next; 
        fast = fast.next; 
    }
    // Now fast points to the start of the loop (inside cycle).
    return fast;
}

LinkedListNode lastNodeOfTheLoop = findStartOfLoop(head);
lastNodeOfTheLoop.next = null; // or lastNodeOfTheLoop.next = head;

🔗 Source: stackoverflow.com

Q18: How to find Nth element from the end of a singly Linked List? ☆☆☆

Topics: Linked Lists

Answer:

Use lockstep solution. The key to this algorithm is to set two pointers p1 and p2 apart by n-1 nodes initially so we want p2 to point to the (n-1)th node from the start of the list then we move p2 till it reaches the last node of the list. Once p2 reaches end of the list p1 will be pointing to the Nth node from the end of the list.

This lockstep approach will generally give better cache utilization, because a node hit by the front pointer may still be in cache when the rear pointer reaches it. In a language implementation using tracing garbage collection, this approach also avoids unnecessarily keeping the beginning (thus entire) list live for the duration of the operation.

Another solution is to use circular buffer. Keep a circular buffer of size x and add the nodes to it as you traverse the list. When you reach the end of the list, the x'th one from the tail is equal to the next entry in the circular buffer.

Complexity Analysis:

Time Complexity: O(n)
Space Complexity: O(n)

The lockstep approach moves all array elements in every step, resulting in a O(n + x2) running time, whereas circular buffer **approach uses a circular array and runs in O(n). The **circular buffer solution requires an additional x in memory.

Implementation:

Java

// Function to return the nth node from the end of a linked list.
// Takes the head pointer to the list and n as input
// Returns the nth node from the end if one exists else returns NULL.
LinkedListNode nthToLast(LinkedListNode head, int n) {
  // If list does not exist or if there are no elements in the list,return NULL
  if (head == null || n < 1) {
    return null;
  }

  // make pointers p1 and p2 point to the start of the list.
  LinkedListNode p1 = head;
  LinkedListNode p2 = head;

  // The key to this algorithm is to set p1 and p2 apart by n-1 nodes initially
  // so we want p2 to point to the (n-1)th node from the start of the list
  // then we move p2 till it reaches the last node of the list. 
  // Once p2 reaches end of the list p1 will be pointing to the nth node 
  // from the end of the list.

  // loop to move p2.
  for (int j = 0; j < n - 1; ++j) { 
   // while moving p2 check if it becomes NULL, that is if it reaches the end
   // of the list. That would mean the list has less than n nodes, so its not 
   // possible to find nth from last, so return NULL.
   if (p2 == null) {
       return null; 
   }
   // move p2 forward.
   p2 = p2.next;
  }

  // at this point p2 is (n-1) nodes ahead of p1. Now keep moving both forward
  // till p2 reaches the last node in the list.
  while (p2.next != null) {
    p1 = p1.next;
    p2 = p2.next;
  }

   // at this point p2 has reached the last node in the list and p1 will be
   // pointing to the nth node from the last..so return it.
   return p1;
 }

Circular buffer approach:

Node getNodeFromTail(Node head, int x) {
  // Circular buffer with current index of of iteration.
  int[] buffer = new int[x];
  int i = 0;

  do {
    // Place the current head in its position in the buffer and increment
    // the head and the index, continuing if necessary.
    buffer[i++ % x] = head;
    head = head.next;
  } while (head.next != NULL);

  // If we haven't reached x nodes, return NULL, otherwise the next item in the
  // circular buffer holds the item from x heads ago.
  return (i < x) ? NULL : buffer[++i % x];
}

🔗 Source: stackoverflow.com

Q19: Implement Double Linked List from Stack with min complexity ☆☆☆

Topics: Linked Lists Stacks

Answer:

Imagine all items are organized into two stacks, draw them facing each other where face is where you put and peek:

1,2,3,4-><-5,6,7,8

now you can move 4 to 5:

1,2,3-><-4,5,6,7,8

and 3 to 4:

1,2-><-3,4,5,6,7,8

and you can go backwards.

You may also need another two stacks so that you can traverse List via the tail:

1,2,3,4 -> <-5,6,7,8 // first pair of stacks
8,7,6,5 -> <-4,3,2,1 // second pair of stacks kept in reverse order

once current stack runs out

empty-><-1,2,3,4,5,6,7,8 // first pair of stacks is currently being traversed
empty-><-8,7,6,5,4,3,2,1 // second pair of stacks

simply switch to the second pair of stacks!

Implementation:

Java

import java.util.Stack;

class DoubleLinkedList{
    Stack<Integer> s;
    Stack<Integer> t;
    int count;
    DoubleLinkedList(){
        s = new Stack<Integer>();
        t = new Stack<Integer>();
        count = 0;
    }

    public void insertInBeginning(int data){
        while(!s.isEmpty()){
            t.push(s.pop());
        }
        s.push(data);
        count++;
    }

    public void insertAtEnd(int data){
        while(!t.isEmpty()){
            s.push(t.pop());
        }
        t.push(data);
        count++;
    }

    public void moveForward(){
        while(!t.isEmpty()){
            int temp = t.pop();
            System.out.println(temp);
            s.push(temp);
        }
    }

    public void moveBackward(){
        while(!s.isEmpty()){
            int temp = s.pop();
            System.out.println(temp);
            t.push(temp);
        }
    }

    public void delete(int data){
        while(!s.isEmpty()){
            t.push(s.pop());
        }
        while(!t.isEmpty()){
            if(t.peek() == data){
                t.pop();
                return;
            }
            else{
                s.push(t.pop());
            }
        }
    }

    public void deleteFirst(){
        while(!s.isEmpty()){
            int temp = s.pop();
            if(s.peek() == null){
                return;
            }
            t.push(temp);
        }
    }

    public void deleteLast(){
        while(!t.isEmpty()){
            int temp = t.pop();
            if(t.peek() == null){
                return;
            }
            s.push(temp);
        }
    }
}

🔗 Source: www.careercup.com

Q20: Merge two sorted singly Linked Lists without creating new nodes ☆☆☆

Topics: Linked Lists

Problem:

You have two singly linked lists that are already sorted, you have to merge them and return a the head of the new list without creating any new extra nodes. The returned list should be sorted as well.

The method signature is:

Node MergeLists(Node list1, Node list2);

Node class is below:

class Node{
   int data;
   Node next;
}

Example:

Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4

Solution:

Here is the algorithm on how to merge two sorted linked lists A and B:

while A not empty or B not empty:
   if first element of A < first element of B:
      remove first element from A
      insert element into C
   end if
   else:
      remove first element from B
      insert element into C
end while

Here C will be the output list.

There are two solutions possible:

• Recursive approach is

  1. Of the two nodes passed, keep the node with smaller value
  2. Point the smaller node's next to the next smaller value of remaining of the two linked lists
  3. Return the current node (which was smaller of the two nodes passed to the method)

• Iterative approach is better for all practical purposes as scales as size of lists swells up:

  1. Treat one of the sorted linked lists as list, and treat the other sorted list as 'bag of nodes'.
  2. Then we lookup for correct place for given node (from bag of nodes) in the list.

Complexity Analysis:

Time Complexity: O(n)

The run time complexity for the recursive and iterative solution here or the variant is O(n).

Implementation:

Java

Recursive solution:

Node MergeLists(Node list1, Node list2) {
  if (list1 == null) return list2;
  if (list2 == null) return list1;

  if (list1.data < list2.data) {
    list1.next = MergeLists(list1.next, list2);
    return list1;
  } else {
    list2.next = MergeLists(list2.next, list1);
    return list2;
  }
}

Recursion should not be needed to avoid allocating a new node:

Node MergeLists(Node list1, Node list2) {
  if (list1 == null) return list2;
  if (list2 == null) return list1;

  Node head;
  if (list1.data < list2.data) {
    head = list1;
  } else {
    head = list2;
    list2 = list1;
    list1 = head;
  }
  while(list1.next != null) {
    if (list1.next.data > list2.data) {
      Node tmp = list1.next;
      list1.next = list2;
      list2 = tmp;
    }
    list1 = list1.next;
  } 
  list1.next = list2;
  return head;
}

PY

Recursive:

def merge_lists(h1, h2):
    if h1 is None:
        return h2
    if h2 is None:
        return h1

    if (h1.value < h2.value):
        h1.next = merge_lists(h1.next, h2)
        return h1
    else:
        h2.next = merge_lists(h2.next, h1)
        return h2

Iterative:

def merge_lists(head1, head2):
    if head1 is None:
        return head2
    if head2 is None:
        return head1

    # create dummy node to avoid additional checks in loop
    s = t = node() 
    while not (head1 is None or head2 is None):
        if head1.value < head2.value:
            # remember current low-node
            c = head1
            # follow ->next
            head1 = head1.next
        else:
            # remember current low-node
            c = head2
            # follow ->next
            head2 = head2.next

        # only mutate the node AFTER we have followed ->next
        t.next = c          
        # and make sure we also advance the temp
        t = t.next

    t.next = head1 or head2

    # return tail of dummy node
    return s.next

🔗 Source: stackoverflow.com

Q21: Sum two numbers represented as Linked Lists ☆☆☆

Topics: Linked Lists

Problem:

You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Example:

Input: (2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 0 -> 8
Explanation: 342 + 465 = 807.

Solution:

You can add two numbers represented using LinkedLists in the same way you add two numbers by hand.

Iterate over the linked lists, add their corresponding elements, keep a carry just the way you do while adding numbers by hand, add the carry-over from the previous addition to the current sum and so on.

One of the trickiest parts of this problem is the issue of the carried number - if every pair of nodes added to a number less than 10, then there wouldn't be a concern of 'carrying' digits over to the next node. However, adding numbers like 4 and 6 produces a carry.

If one list is longer than the other, we still will want to add the longer list's nodes to the solution, so we'll have to make sure we continue to check so long as the nodes aren't null. That means the while loop should keep going as long as list 1 isn't null OR list 2 isn't null.

Implementation:

Java

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    ListNode head = new ListNode(0);
    ListNode result = head;
    int carry = 0;

    while (l1 != null || l2 != null || carry > 0) {
        int resVal = (l1 != null? l1.val : 0) + (l2 != null? l2.val : 0) + carry;
        result.next = new ListNode(resVal % 10);
        carry = resVal / 10;
        l1 = (l1 == null ? l1 : l1.next);
        l2 = (l2 == null ? l2 : l2.next);
        result = result.next;
    }

    return head.next;
}

PY

class Solution:
# @return a ListNode
def addTwoNumbers(self, l1, l2):
    carry = 0
    root = n = ListNode(0)
    while l1 or l2 or carry:
        v1 = v2 = 0
        if l1:
            v1 = l1.val
            l1 = l1.next
        if l2:
            v2 = l2.val
            l2 = l2.next
        carry, val = divmod(v1+v2+carry, 10)
        n.next = ListNode(val)
        n = n.next
    return root.next

🔗 Source: dev.to

Q22: When to use a Linked List over an Array/Array List? ☆☆☆

Topics: Arrays Linked Lists

Answer:

Linked lists are preferable over arrays when:

1. you need constant-time insertions/deletions from the list (such as in real-time computing where time predictability is absolutely critical)
2. you don't know how many items will be in the list. With arrays, you may need to re-declare and copy memory if the array grows too big
3. you don't need random access to any elements
4. you want to be able to insert items in the middle of the list (such as a priority queue)

Arrays are preferable when:

1. you need indexed/random access to elements
2. you know the number of elements in the array ahead of time so that you can allocate the correct amount of memory for the array
3. you need speed when iterating through all the elements in sequence. You can use pointer math on the array to access each element, whereas you need to lookup the node based on the pointer for each element in linked list, which may result in page faults which may result in performance hits.
4. memory is a concern. Filled arrays take up less memory than linked lists. Each element in the array is just the data. Each linked list node requires the data as well as one (or more) pointers to the other elements in the linked list.

Array Lists (like those in .Net) give you the benefits of arrays, but dynamically allocate resources for you so that you don't need to worry too much about list size and you can delete items at any index without any effort or re-shuffling elements around. Performance-wise, arraylists are slower than raw arrays.

🔗 Source: stackoverflow.com

Q23: Why does linked list delete and insert operation have complexity of O(1)? ☆☆☆

Topics: Linked Lists

Answer:

When you are inserting a node in the middle of a linked list, the assumption taken is that you are already at the address where you have to insert the node. Indexing is considered as a separate operation. So insertion is itself O(1), but getting to that middle node is O(n). Thus adding to a linked list does not require a traversal, as long as you know a reference.

🔗 Source: stackoverflow.com

Q24: Find Merge (Intersection) Point of Two Linked Lists ☆☆☆☆

Topics: Linked Lists

Problem:

Say, there are two lists of different lengths, merging at a point; how do we know where the merging point is?

Conditions:

1. We don't know the length

Solution:

This arguably violates the "parse each list only once" condition, but implement the tortoise and hare algorithm (used to find the merge point and cycle length of a cyclic list) so you start at List 1, and when you reach the NULL at the end you pretend it's a pointer to the beginning of List 2, thus creating the appearance of a cyclic list. The algorithm will then tell you exactly how far down List 1 the merge is.

Algorithm steps:

• Make an interating pointer like this:
  • it goes forward every time till the end, and then
  • jumps to the beginning of the opposite list, and so on.
• Create two of these, pointing to two heads.
• Advance each of the pointers by 1 every time, until they meet in intersection point (IP). This will happen after either one or two passes.

To understand it count the number of nodes traveled from head1-> tail1 -> head2 -> intersection point and head2 -> tail2-> head1 -> intersection point. Both will be equal (Draw diff types of linked lists to verify this). Reason is both pointers have to travel same distances head1-> IP + head2->IP before reaching IP again. So by the time it reaches IP, both pointers will be equal and we have the merging point.

Implementation:

CS

int FindMergeNode(Node headA, Node headB) {
    Node currentA = headA;
    Node currentB = headB;

    //Do till the two nodes are the same
    while(currentA != currentB){
        //If you reached the end of one list start at the beginning of the other one
        //currentA
        if(currentA.next == null){
            currentA = headB;
        }else{
            currentA = currentA.next;
        }
        //currentB
        if(currentB.next == null){
            currentB = headA;
        }else{
            currentB = currentB.next;
        }
    }
    return currentB.data;
}

Java

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    //boundary check
    if(headA == null || headB == null) return null;

    ListNode a = headA;
    ListNode b = headB;

    //if a & b have different len, then we will stop the loop after second iteration
    while( a != b){
        //for the end of first iteration, we just reset the pointer to the head of another linkedlist
        a = a == null? headB : a.next;
        b = b == null? headA : b.next;    
    }

    return a;
}

PY

# the idea is if you switch head, the possible difference between length would be countered. 
# On the second traversal, they either hit or miss. 
# if they meet, pa or pb would be the node we are looking for, 
# if they didn't meet, they will hit the end at the same iteration, pa == pb == None, return either one of them is the same,None

class Solution:
    # @param two ListNodes
    # @return the intersected ListNode
    def getIntersectionNode(self, headA, headB):
        if headA is None or headB is None:
            return None

        pa = headA # 2 pointers
        pb = headB

        while pa is not pb:
            # if either pointer hits the end, switch head and continue the second traversal, 
            # if not hit the end, just move on to next
            pa = headB if pa is None else pa.next
            pb = headA if pb is None else pb.next

        return pa # only 2 ways to get out of the loop, they meet or the both hit the end=None

🔗 Source: stackoverflow.com

Q25: Find the length of a Linked List which contains cycle (loop) ☆☆☆☆

Topics: Linked Lists

Answer:

1. To find the length of loop apply Tortoise and Hare algorithm:

• Pointer A advances one (1) node a time.
• Pointer B advanced two (2) node a time.
• Start from head, they advanced at the same time until B hit null (no loop) or A and B point to the same node.

1. Now, has A advances only, A would meet B again. From that you can find the length of the loop say L.
2. Start from head again, this time have a pointer C advances L nodes first, followed by pointer D behind it, each advances one node at a time.
3. When they meet, the number of nodes D traveled L0 plus L is equal to the length of the linked list with a loop.

Implementation:

Java

package com.farenda.tutorials.algorithms.lists;

public class FloydCycleDetector {

    private int position;
    private int length;
    private boolean cycle;
    private Node head, tortoise, hare;

    public void detect(Node head) {
        this.head = head;
        this.tortoise = this.hare = head;
        this.cycle = detectCycle();
        if (cycle) {
            System.out.println("Found cycle.");
            this.position = findPosition();
            this.length = cycleLength();
        } else {
            System.out.println("No cycle.");
            this.position = -1;
            this.length = 0;
        }
    }

    public boolean hasCycle() {
        return cycle;
    }

    public int length() {
        return length;
    }

    public int position() {
        return position;
    }

    private boolean detectCycle() {
        if (tortoise == null || tortoise.next == null) {
            return false;
        }
        while (hare != null && hare.next != null) {
            System.out.printf("(%d, %d),", tortoise.data, hare.data);
            tortoise = tortoise.next;
            hare = hare.next.next;
            if (tortoise == hare) {
                System.out.printf("turtle(%d) == hare(%d)%n",
                        tortoise.data, hare.data);
                return true;
            }
        }
        return false;
    }

    private int findPosition() {
        int i = 1;
        tortoise = head;
        System.out.printf("(%d, %d),", tortoise.data, hare.data);
        while (tortoise != hare) {
            tortoise = tortoise.next;
            hare = hare.next;
            ++i;
        }
        return i;
    }

    private int cycleLength() {
        int i = 0;
        do {
            hare = hare.next;
            ++i;
        } while (tortoise != hare);
        return i;
    }
}

PY

nodes = [(1, 2), (2, 3), (3, 4), (4, 5), (5, 2)]

def next(parent):
  def find(nodes, parent):
    current = nodes[0]
    rest = nodes[1:]

    if current and current[0] == parent:
      return current[1]
    else:
      return find(rest, parent)
  return find(nodes, parent) 

def next_next(x):
  return next(next(x))

def meet(slow, fast, p1, p2, steps):
  p1 = slow(p1)
  p2 = fast(p2)
  steps = steps + 1

  if p1 == p2:
    return (p1, steps)
  else:
    return meet(slow, fast, p1, p2, steps)

def meet_result(slow, fast, p1, p2):
  result = meet(slow, fast, p1, p2, 0)
  return result[0]

def meet_count(slow, fast, p1, p2):
  result = meet(slow, fast, p1, p2, 0)
  return result[1]

def find_cycle(init):
  cycle_meet = meet_result(next, next_next, init, init)
  cycle_root = meet_result(next, next, cycle_meet, init)
  cycle_length = meet_count(lambda x: x, next, cycle_root, cycle_root)
  return (cycle_meet, cycle_root, cycle_length)

🔗 Source: www.careercup.com

Q26: Given a singly Linked List, determine if it is a Palindrome ☆☆☆☆

Topics: Linked Lists

Problem:

Could you do it in O(1) time and O(1) space?

Solution:

Solution: is Reversed first half **== **Second half?

Let's look to an example [1, 1, 2, 1]. In the beginning, set two pointers fast and slow starting at the head.

1 -> 1 -> 2 -> 1 -> null
sf

(1) Move: fast pointer goes to the end, and slow goes to the middle.

1 -> 1 -> 2 -> 1 -> null
          s          f

(2) Reverse: the right half is reversed, and slow pointer becomes the 2nd head.

1 -> 1    null <- 2 <- 1
h                      s

(3) Compare: run the two pointers head and slow together and compare.

1 -> 1    null <- 2 <- 1
     h            s

Implementation:

Java

public boolean isPalindrome(ListNode head) {
    ListNode fast = head, slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    if (fast != null) { // odd nodes: let right half smaller
        slow = slow.next;
    }
    slow = reverse(slow);
    fast = head;

    while (slow != null) {
        if (fast.val != slow.val) {
            return false;
        }
        fast = fast.next;
        slow = slow.next;
    }
    return true;
}

public ListNode reverse(ListNode head) {
    ListNode prev = null;
    while (head != null) {
        ListNode next = head.next;
        head.next = prev;
        prev = head;
        head = next;
    }
    return prev;
}

PY

# Note: while comparing the two halves, restore the list to its original 
# state by reversing the first half back.

def isPalindrome(self, head):
    rev = None
    fast = head
    while fast and fast.next:
        fast = fast.next.next
        rev, rev.next, head = head, rev, head.next
    tail = head.next if fast else head
    isPali = True
    while rev:
        isPali = isPali and rev.val == tail.val
        head, head.next, rev = rev, head, rev.next
        tail = tail.next
    return isPali

🔗 Source: stackoverflow.com

Q27: How is it possible to do Binary Search on a Doubly-Linked List in O(n) time? ☆☆☆☆

Topics: Searching Linked Lists

Problem:

I've heard that it's possible to implement binary search over a doubly-linked list in O(n) time. Accessing a random element of a doubly-linked list takes O(n) time, and binary search accesses O(log n) different elements, so shouldn't the runtime be O(log n)) instead?

Solution:

It's technically correct to say that the runtime of binary search on a doubly-linked list is O(log n)), but that's not a tight upper bound. Using a slightly better implementation of binary search and a more clever analysis, it's possible to get binary search to run in time O(n).

The basic idea behind binary search is the following:

• If the list is empty, the element being searched for doesn't exist.
• Otherwise:
  • Look at the middle element.
  • If it matches the element in question, return it.
  • If it's bigger than the element in question, discard the back half of the list.
  • If it's smaller than the element in question, discard the front half of the list.

A naive implementation of binary search on a doubly-linked list would work by computing the indices to look up on each iteration (just like in the array case), then access each one by starting at the front of the list and scanning forward the appropriate number of steps. This is indeed very slow.

We can speed this up by a factor of Θ(log n) by being more clever with our approach. The reason the previous algorithm is slow is that every time we need to look up an element, we start the search from the beginning of the array. However, we don't need to do this. After looking up the middle element the first time, we're already in the middle of the array, and we know that the next lookup we're going to make will be either at position n / 4 or 3n / 4, which is only distance n / 4 from where we left off (compared to n / 4 or 3n / 4 if we start from the beginning of the array). What if we just trekked out from our stopping position (n / 2) to the next position, rather than restarting at the front of the list?

Here's our new algorithm. Begin by scanning to the middle of the array, which requires n / 2 steps. Then, determine whether to visit the element at the middle of the first half of the array or the middle of the second half of the array. Reaching there from position n / 2 only requires n / 4 total steps. From there, going to the midpoint of the quarter of the array containing the element takes only n / 8 steps, and going from there to the midpoint of the eighth of the array containing the element takes only n / 16 steps, etc. This means that the total number of steps made is given by

n / 2 + n / 4 + n / 8 + n / 16 + ...

= n (1/2 + 1/4 + 1/8 + ...)

≤ n

This follows from the fact that the sum of the infinite geometric series 1/2 + 1/4 + 1/8 + ... is 1. Therefore, the total work done in the worst case only Θ(n), which is much better than the Θ(n log n) worst case from before.

🔗 Source: stackoverflow.com

Q28: How to apply Binary Search O(log n) on a sorted Linked List? ☆☆☆☆

Topics: Searching Linked Lists

Problem:

Sorted singly linked list is given and we have to search one element from this list. Time complexity should not be more than O(log n). How would you apply binary search on a sorted linked list?

Solution:

It is certainly not possible with a plain singly-linked list. As linked list does not provide random access if we try to apply binary search algorithm it will reach O(n) as we need to find length of the list and go to the middle. To avoid this problem you need to use skip list.

🔗 Source: FullStack.Cafe

Q29: How to recursively reverse a Linked List? ☆☆☆☆

Topics: Linked Lists Recursion

Answer:

Start from the bottom up by asking and answering tiny questions:

• What is the reverse of null (the empty list)? null.
• What is the reverse of a one element list? the element.
• What is the reverse of an n element list? the reverse of the rest of the list followed by the first element.

P.S.

How to understand that part?

head.next.next = head;
head.next = null;

Think about the origin link list:

1->2->3->4->5

Now assume that the last node has been reversed. Just like this:

1->2->3->4<-5

And this time you are at the node 3 , you want to change 3->4 to 3<-4 , means let 3->next->next = 3 (as 3->next is 4 and 4->next = 3 is to reverse it)

Complexity Analysis:

Time Complexity: O(n)
Space Complexity: O(n)

Assume that n is the list's length, the time complexity is O(n). The extra space comes from implicit stack space due to recursion. The recursion could go up to n levels deep then space complexity is O(n).

Implementation:

JS

var reverseList = function(head) {
    if (!head) {
        return head;
    }
    let pre = head.next;
    head.next = null;
    return fun(head, pre);

    function fun(cur, pre) {
        if (pre == null) {
            return cur;
        }
        let tmp = pre.next;
        pre.next = cur;
        return fun(pre, tmp);
    }
}

Java

Node reverse(Node head) {
  // if head is null or only one node, it's reverse of itself.
  if ( (head == null) || (head.next == null) ) return head;

  // reverse the sub-list leaving the head node.
  Node reverse = reverse(head.next);

  // head.next still points to the last element of reversed sub-list.
  // so move the head to end.
  head.next.next = head;

  // point last node to nil, (get rid of cycles)
  head.next = null;
  return reverse;
}

PY

class Solution(object):
    def reverseList(self, head):  # Recursive
        """
        :type head: ListNode
        :rtype: ListNode
        """     
        if not head or not head.next:
            return head
        p = self.reverseList(head.next)
        head.next.next = head
        head.next = None
        return p 

🔗 Source: stackoverflow.com

Q30: How would you traverse a Linked List in O(n1/2)? ☆☆☆☆

Topics: Linked Lists

Answer:

Traversal more efficient than O(n) is not possible, since "traversal" requires accessing each node in turn.

It is possible to make random access faster than O(n) though, by maintaining a second linked list that retains links to intermediate nodes; insertion, deletion, and appending cost will go up though, due to the increased complexity of maintenance of the second list.

🔗 Source: stackoverflow.com

Q31: Why is Merge sort preferred over Quick sort for sorting Linked Lists? ☆☆☆☆

Topics: Linked Lists Sorting

Answer:

• Quicksort depends on being able to index (or random access) into an array or similar structure. When that's possible, it's hard to beat Quicksort.
• You can't index directly into a linked list very quickly. That is, if myList is a linked list, then myList[x], were it possible to write such syntax, would involve starting at the head of the list and following the first x links. That would have to be done twice for every comparison that Quicksort makes, and that would get expensive real quick.
• Same thing on disk - Quicksort would have to seek and read every item it wants to compare.
• Merge sort is faster in these situations because it reads the items sequentially, typically making log(n) passes over the data. There is much less I/O involved, and much less time spent following links in a linked list.
• Quicksort is fast when the data fits into memory and can be addressed directly. Mergesort is faster when data won't fit into memory or when it's expensive to get to an item.

🔗 Source: stackoverflow.com

Q32: Do you know any better than than Floyd's algorithm for cycle detection? ☆☆☆☆☆

Topics: Linked Lists

Answer:

Richard Brent described an alternative cycle detection algorithm, which is pretty much like the hare and the tortoise Floyd's cycle except that, the slow node here doesn't move, but is later "teleported" to the position of the fast node at fixed intervals.

Brent claims that his algorithm is 24% to 36% faster than the Floyd's cycle algorithm.

Complexity Analysis:

Time Complexity: O(n)
Space Complexity: O(n)

Implementation:

Java

public static boolean hasLoop(Node root) {
    if (root == null) return false;

    Node slow = root, fast = root;
    int taken = 0, limit = 2;

    while (fast.next != null) {
        fast = fast.next;
        taken++;
        if (slow == fast) return true;

        if (taken == limit) {
            taken = 0;
            limit <<= 1; // equivalent to limit *= 2;
            slow = fast; // teleporting the turtle (to the hare's position) 
        }
    }
    return false;
}

🔗 Source: stackoverflow.com

Thanks 🙌 for reading and good luck on your interview! Please share this article with your fellow Devs if you like it! Check more FullStack Interview Questions & Answers on 👉 www.fullstack.cafe