Dynamic programming is all about ordering your computations in a way that avoids recalculating duplicate work. More specifically, Dynamic Programming is a technique used to avoid computing multiple times the same subproblem in a recursive algorithm. DP algorithms could be implemented with recursion, but they don't have to be. Follow along and learn 12 Most Common Dynamic Programming Interview Questions and Answers to nail your next coding interview.
🔴 Originally published on FullStack.Cafe - Kill Your Next Tech Interview
Q1: What is Dynamic Programming? ☆
Topics: Dynamic Programming
Answer:
Dynamic programming is all about ordering your computations in a way that avoids recalculating duplicate work. More specifically, Dynamic Programming is a technique used to avoid computing multiple times the same subproblem in a recursive algorithm. DP algorithms could be implemented with recursion, but they don't have to be.
With dynamic programming, you store your results in some sort of table generally. When you need the answer to a problem, you reference the table and see if you already know what it is. If not, you use the data in your table to give yourself a stepping stone towards the answer.
There are two approaches to apply Dynamic Programming:
- The top-down or memoization. When the recursion does a lot of unecessary calculation, an easy way to solve this is to cache the results and to check before executing the call if the result is already in the cache.
- The bottom-up or tabulation approach. A better way to do this is to get rid of the recursion all-together by evaluating the results in the right order and building the array as we iterate. The partial results are available when needed if the iteration is done in the right order.
TOP of the tree
fib(4)
fib(3)...................... + fib(2)
fib(2)......... + fib(1) fib(1)........... + fib(0)
fib(1) + fib(0) fib(1) fib(1) fib(0)
fib(1) fib(0)
BOTTOM of the tree
🔗 Source: stackoverflow.com
Q2: How Dynamic Programming is different from Recursion and Memoization? ☆☆
Topics: Dynamic Programming Recursion
Answer:
- Memoization is when you store previous results of a function call (a real function always returns the same thing, given the same inputs). It doesn't make a difference for algorithmic complexity before the results are stored.
- Recursion is the method of a function calling itself, usually with a smaller dataset. Since most recursive functions can be converted to similar iterative functions, this doesn't make a difference for algorithmic complexity either.
-
Dynamic programming is the process of solving easier-to-solve sub-problems and building up the answer from that. Most DP algorithms will be in the running times between a Greedy algorithm (if one exists) and an exponential (enumerate all possibilities and find the best one) algorithm.
- DP algorithms could be implemented with recursion, but they don't have to be.
- DP algorithms can't be sped up by memoization, since each sub-problem is only ever solved (or the "solve" function called) once.
🔗 Source: stackoverflow.com
Q3: What are pros and cons of Memoization or Top-Down approach? ☆☆
Topics: Dynamic Programming
Answer:
Pros:
- Memoization is very easy to code (you can generally* write a "memoizer" annotation or wrapper function that automatically does it for you), and should be your first line of approach. It feels more natural. You can take a recursive function and memoize it by a mechanical process (first lookup answer in cache and return it if possible, otherwise compute it recursively and then before returning, you save the calculation in the cache for future use), whereas doing bottom up dynamic programming requires you to encode an order in which solutions are calculated.
- Top-down only solves sub-problems used by your solution whereas bottom-up might waste time on redundant sub-problems.
Cons:
- With memoization, if the tree is very deep (e.g.
fib(106)), you will run out of stack space, because each delayed computation must be put on the stack, and you will have106of them.
🔗 Source: stackoverflow.com
Q4: What are some characteristics of Dynamic Programming? ☆☆
Topics: Dynamic Programming
Answer:
The key idea of DP is to save answers of overlapping smaller sub-problems to avoid recomputation. For that:
- An instance is solved using the solutions for smaller instances.
- The solutions for a smaller instance might be needed multiple times, so store their results in a table.
- Thus each smaller instance is solved only once.
- Additional space is used to save time.
🔗 Source: stackoverflow.com
Q5: LIS: Find length of the longest increasing subsequence (LIS) in the array. Solve using DP. ☆☆☆
Topics: Dynamic Programming
Problem:
The longest increasing subsequence problem is to find a subsequence of a given sequence in which the subsequence's elements are in sorted order, lowest to highest, and in which the subsequence is as long as possible.
Consider:
In the first 16 terms of the binary Van der Corput sequence
0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15
a longest increasing subsequence is
0, 2, 6, 9, 11, 15.
This subsequence has length six;
the input sequence has no seven-member increasing subsequences.
The longest increasing subsequence in this example is not unique: for
instance,
0, 4, 6, 9, 11, 15 or
0, 2, 6, 9, 13, 15 or
0, 4, 6, 9, 13, 15
are other increasing subsequences of equal length in the same
input sequence.
Solution:
- Let's assume the indices of the array are from 0 to N - 1.
- Let's define
DP[i]to be the length of the LIS (Longest increasing subsequence) which is ending at element with indexi.
DP[0] = 1; // length of LIS for the first element is always 1
int maxLength = 1;
- To compute
DP[i]for eachi > 0we look at all indicesj < iand check both:- if
DP[j] + 1 > DP[i]and -
array[j] < array[i](we want it to be increasing). - If this is
truewe can update the current optimum forDP[i].
- if
for (int i = 1; i < N; i++)
{
DP[i] = 1;
prev[i] = -1;
for (int j = i - 1; j >= 0; j--)
if (DP[j] + 1 > DP[i] && array[j] < array[i])
{
DP[i] = DP[j] + 1;
prev[i] = j;
}
if (DP[i] > maxLength)
{
bestEnd = i;
maxLength = DP[i];
}
}
- To find the global optimum for the array you can take the maximum value from DP
[0...N - 1] - Use the array
prevto be able later to find the actual sequence not only its length. Just go back recursively frombestEndin a loop usingprev[bestEnd]. The-1value is a sign to stop.
Complexity Analysis:
Time Complexity: O(n^2)
Space Complexity: O(n^2)
- Time complexity :
O(n^2). Two loops ofnare there. - Space complexity :
O(n). DP array of sizenis used. ### Implementation: #### JS
/**
* Dynamic programming approach to find longest increasing subsequence.
* Complexity: O(n * n)
*
* @param {number[]} sequence
* @return {number}
*/
export default function dpLongestIncreasingSubsequence(sequence) {
// Create array with longest increasing substrings length and
// fill it with 1-s that would mean that each element of the sequence
// is itself a minimum increasing subsequence.
const lengthsArray = Array(sequence.length).fill(1);
let previousElementIndex = 0;
let currentElementIndex = 1;
while (currentElementIndex < sequence.length) {
if (sequence[previousElementIndex] < sequence[currentElementIndex]) {
// If current element is bigger then the previous one then
// current element is a part of increasing subsequence which
// length is by one bigger then the length of increasing subsequence
// for previous element.
const newLength = lengthsArray[previousElementIndex] + 1;
if (newLength > lengthsArray[currentElementIndex]) {
// Increase only if previous element would give us bigger subsequence length
// then we already have for current element.
lengthsArray[currentElementIndex] = newLength;
}
}
// Move previous element index right.
previousElementIndex += 1;
// If previous element index equals to current element index then
// shift current element right and reset previous element index to zero.
if (previousElementIndex === currentElementIndex) {
currentElementIndex += 1;
previousElementIndex = 0;
}
}
// Find the biggest element in lengthsArray.
// This number is the biggest length of increasing subsequence.
let longestIncreasingLength = 0;
for (let i = 0; i < lengthsArray.length; i += 1) {
if (lengthsArray[i] > longestIncreasingLength) {
longestIncreasingLength = lengthsArray[i];
}
}
return longestIncreasingLength;
}
Java
public int longestIncreasingSubsequence(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int n = nums.length;
int[] dp = new int[n];
int max = 0;
for (int i = 0; i < n; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[j] <= nums[i]) {
dp[i] = dp[i] > dp[j] + 1 ? dp[i] : dp[j] + 1;
}
}
if (dp[i] > max) {
max = dp[i];
}
}
return max;
}
PY
Traditional DP solution.
# Time: O(n^2)
# Space: O(n)
# Traditional DP solution.
class SolutionDP(object):
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
dp = [] # dp[i]: the length of LIS ends with nums[i]
for i in xrange(len(nums)):
dp.append(1)
for j in xrange(i):
if nums[j] < nums[i]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp) if dp else 0
Or in 5 lines of code:
def lis(a):
L = []
for (k,v) in enumerate(a):
L.append(max([L[i] for (i,n) in enumerate(a[:k]) if n<v] or [[]], key=len) + [v])
return max(L, key=len)
inp = [int(a) for a in input("List of integers: ").split(' ')]
print(lis(inp));
🔗 Source: stackoverflow.com
Q6: Provide an example of Dynamic Program but without Recursion ☆☆☆
Topics: Dynamic Programming
Answer:
The following would be considered DP, but without recursion (using bottom-up or tabulation DP approach).
int fibresult[N];
void setup_fib()
{
fibresult[0] = 1;
fibresult[1] = 1;
for (int i = 2; i < N; i++)
fibresult[i] = fibresult[i-1] + fibresult[i-2];
}
int fib(int x) { return fibresult[x]; }
This way may be described as "eager", "precaching" or "iterative". Its faster overall but we have to manually figure out the order the subproblems need to be calculated in. This is easy for fibonacci, but for more complex DP problems it gets harder, and so we fall back to the lazy recursive method if it is fast enough.
🔗 Source: stackoverflow.com
Q7: What are some pros and cons of Tabulation or Bottom-Up approach? ☆☆☆
Topics: Dynamic Programming
Answer:
Pros:
- If you are doing an extremely complicated problems, you might have no choice but to do tabulation (or at least take a more active role in steering the memoization where you want it to go). Also if you are in a situation where optimization is absolutely critical and you must optimize, tabulation will allow you to do optimizations which memoization would not otherwise let you do in a sane way.
- Why? Because with memoization, if the tree is very deep (e.g. fib(10^6)), you will run out of stack space, because each delayed computation must be put on the stack, and you will have 10^6 of them.
- In many applications the bottom-up approach is slightly faster because of the overhead of recursive calls.
Cons:
- The downside of tabulation is that you have to come up with an ordering. You must pick, ahead of time, the exact order in which you will do your computations.
- Top-down only solves sub-problems used by your solution whereas bottom-up might waste time on redundant sub-problems.
🔗 Source: stackoverflow.com
Q8: What is the difference between Divide and Conquer and Dynamic Programming Algorithms? ☆☆☆
Topics: Divide & Conquer Dynamic Programming
Answer:
Dynamic programming is an extension of Divide and Conquer paradigm.
- They both work by recursively breaking down a problem into two or more sub-problems. The solutions to the sub-problems are then combined to give a solution to the original problem.
- In Divide and conquer the sub-problems are independent of each other. Mergesort is a classic example of divide and conquer. The main difference between this example and the Fibonacci example is that in a mergesort, the division can (theoretically) be arbitrary, and no matter how you slice it up, you are still merging and sorting.
- In dynamic programming the sub-problem are not independent. So to calculate new Fib number you have to know two previous values. For Merge sort you don't need to know the sorting order of previously sorted sub-array to sort another one.
- Dynamic programming approach may be applied to the problem only if the problem has certain restrictions or prerequisites:
- Optimal substructure — optimal solution can be constructed from optimal solutions of its subproblems
- Overlapping sub-problems — problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblems.
- Dynamic programming approach extends divide and conquer approach with two techniques:
- memoization (top-down cache filling)
- tabulation (bottom-up cache filling)
🔗 Source: stackoverflow.com
Q9: What should you consider when choosing between Top-Down vs Bottom-Up solutions for the same problem? ☆☆☆
Topics: Dynamic Programming
Answer:
Two things to consider when deciding which algorithm to use
- Time Complexity. Both approaches have the same time complexity in general, but because for loop is cheaper than recursive function calls, bottom-up can be faster if measured in machine time.
-
Space Complexity. (without considering extra call stack allocations during top-down) Usually both approaches need to build a table for all sub-solutions, but bottom-up is following a topological order, its cost of auxiliary space can be sometimes reduced to the size of problem's immediate dependencies. For example:
fibonacci(n) = fibonacci(n-1) + fibonacci(n-2), we only need to store the past two calculations
That being said, bottom-up is not always the best choice, I will try to illustrate with examples:
- Top-down only solves sub-problems used by your solution whereas bottom-up might waste time on redundant sub-problems. A silly example would be 0-1 knapsack with 1 item...run time difference is
O(1)vsO(weight) - you might need to perform extra work to get topological order for bottm-up. In Longest Increasing Path in Matrix if we want to do sub-problems after their dependencies, we would have to sort all entries of the matrix in descending order, that's extra
nmlog(nm)pre-processing time before DP
🔗 Source: stackoverflow.com
Q10: Compare Greedy vs Divide & Conquer vs Dynamic Programming Algorithms ☆☆☆☆
Topics: Divide & Conquer Dynamic Programming Greedy Algorithms
Answer:
Consider:
| Greedy | Divide & Conquer | Dynamic Programming |
|---|---|---|
| Optimises by making the best choice at the moment | Optimises by breaking down a subproblem into simpler versions of itself and using multi-threading & recursion to solve | Same as Divide and Conquer, but optimises by caching the answers to each subproblem as not to repeat the calculation twice. |
| Doesn't always find the optimal solution, but is very fast | Always finds the optimal solution, but is slower than Greedy | Always finds the optimal solution, but could be pointless on small datasets. |
| Requires almost no memory | Requires some memory to remember recursive calls | Requires a lot of memory for memoisation / tabulation |
🔗 Source: skerritt.blog
Q11: How to use Memoization for N-th Fibonacci number? ☆☆☆☆
Topics: Dynamic Programming Fibonacci Series Recursion
Problem:
Why? Any problems you may face with that solution?
Solution:
Yes. It's called Memoization. Memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls.
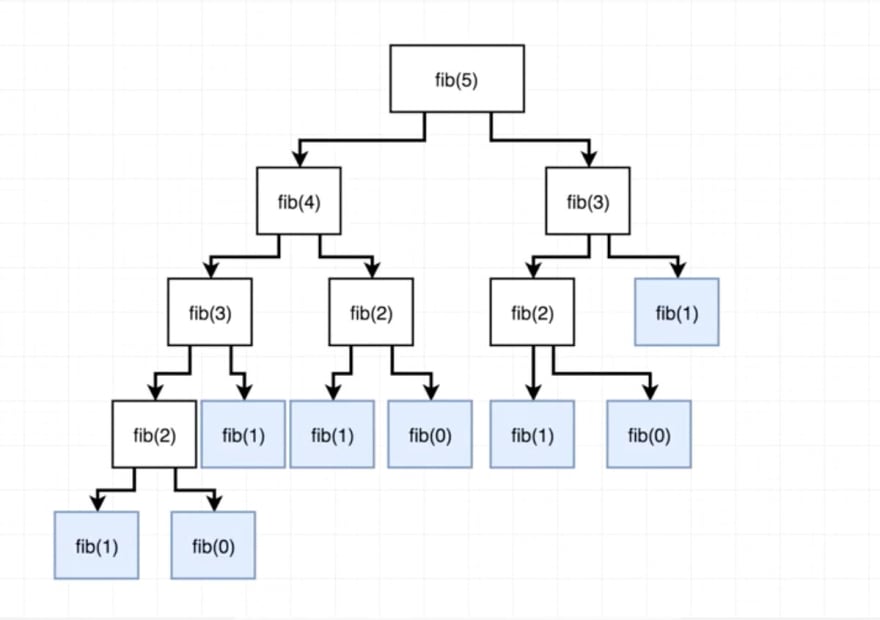
Let’s look at the diagram that will help you understand what’s going on here with the rest of our code. Function fib is called with argument 5. Can you see that we calculate the fib(2) results 3(!) times?
Basically, if we just store the value of each index in a hash, we will avoid the computational time of that value for the next N times. This change will increase the space complexity of our new algorithm to O(n) but will dramatically decrease the time complexity to 2N which will resolve to linear time since 2 is a constant O(n).
There’s just one problem: With an infinite series, the memo array will have unbounded growth. Eventually, you’re going to run into heap size limits, and that will crash the JS engine. No worries though. With Fibonacci, you’ll run into the maximum exact JavaScript integer size first, which is 9007199254740991. That’s over 9 quadrillion, which is a big number, but Fibonacci isn’t impressed. Fibonacci grows fast. You’ll burst that barrier after generating only 79 numbers.
Complexity Analysis:
Time Complexity: O(n)
Space Complexity: O(n)
Implementation:
JS
function fibonacci(num, memo) {
memo = memo || {};
if (memo[num]) return memo[num];
if (num <= 1) return 1;
return memo[num] = fibonacci(num - 1, memo) + fibonacci(num - 2, memo);
}
Java
static int fibMemo[];
public static int fibByRecMemo(int num) {
if (num == 0) {
fibMemo[0] = 0;
return 0;
}
if (num == 1 || num == 2) {
fibMemo[num] = 1;
return 1;
}
if (fibMemo[num] == 0) {
fibMemo[num] = fibByRecMemo(num - 1) + fibByRecMemo(num - 2);
return fibMemo[num];
} else {
return fibMemo[num];
}
}
🔗 Source: medium.com
Q12: Is Dijkstra's algorithm a Greedy or Dynamic Programming algorithm? ☆☆☆☆
Topics: Greedy Algorithms Dynamic Programming
Answer:
Both.
- It's greedy because you always mark the closest vertex.
- It's dynamic because distances are updated using previously calculated values.
But would say it's definitely closer to dynamic programming than to a greedy algorithm. To find the shortest distance from A to B, it does not decide which way to go step by step. Instead, it finds all places that one can go from A, and marks the distance to the nearest place. Marking that place, however, does not mean you'll go there. It only means that distance can no longer be made shorter assuming all edges of the graph are positive. The algorithm itself does not have a good sense of direction as to which way will get you to place B faster. The optimal decisions are not made greedily, but are made by exhausting all possible routes that can make a distance shorter. Therefore, it's a dynamic programming algorithm, the only variation being that the stages are not known in advance, but are dynamically determined during the course of the algorithm. You can call it a "dynamic" dynamic programming algorithm, if you like, to tell it apart from other dynamic programming algorithms with predetermined stages of decision making to go through
🔗 Source: stackoverflow.com
Thanks 🙌 for reading and good luck on your interview! Please share this article with your fellow Devs if you like it! Check more FullStack Interview Questions & Answers on 👉 www.fullstack.cafe




Top comments (0)