Link to the solution

Link to the problem

1. Introduction

I was able to figure out the brute force solution using dynamic programming, which was pretty intuitive. But I could not figure out how to implement the memoization to my solution. I found out one of the solutions & explanation from the problem's discussion page and I would like to share it with you guys.

2. Problem Explanation

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

My understanding

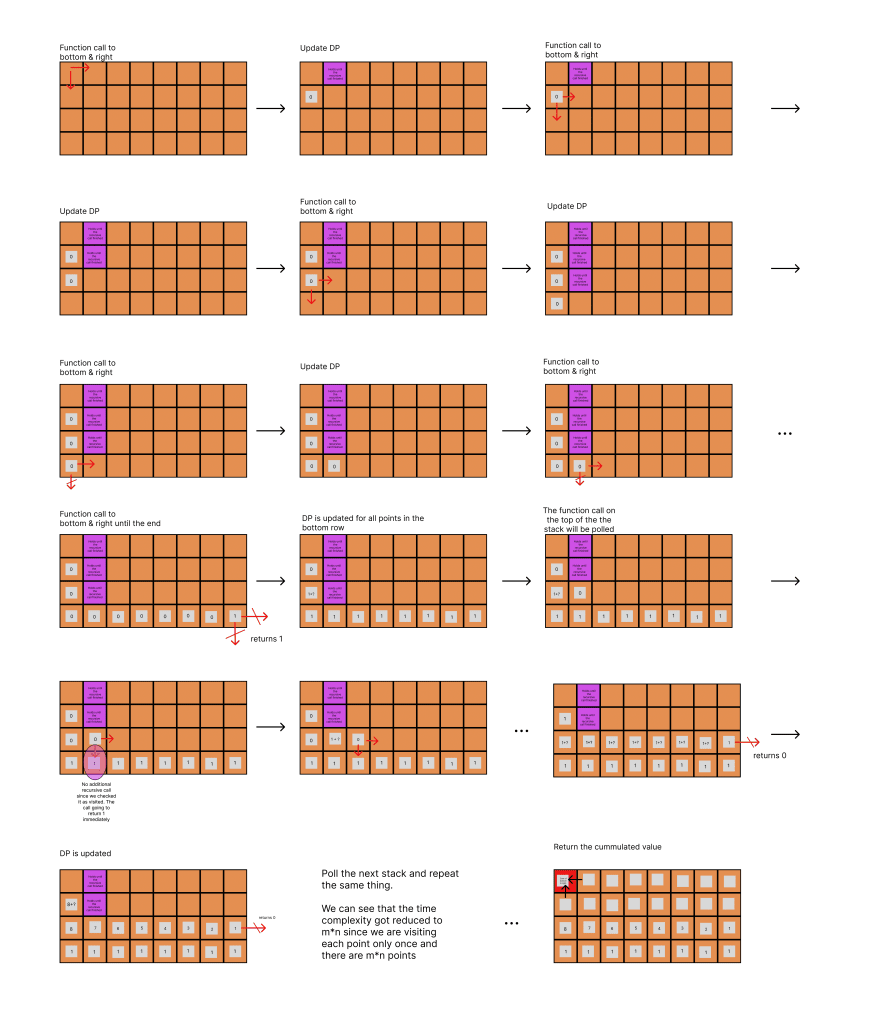
Since there were only two direction to check for each grid, I used recursion until the passed row and column indices are either out of the range or on the destination grid. And return 1 if the function reached to the destination and return 0 else.

At the end of the function, I am returning the sum of two recursive calls which are checking right side block and down side block respectively.

My brute force solution⬇️ (the solution will eventually get time limit exceeded error on Leetcode)

class Solution {
public:
    int uniquePaths(int m, int n) { 
        return findPaths(m,n,0,0);
    }

    int findPaths(int m, int n, int row, int col){

        // Checking out bound error
        if(row < 0 || col < 0 || row >= m || col >= n) return 0;

        // Checking if the function reached to the destination
        if(row == m-1 && col == n-1) return 1;

        // return the sum of paths
        return findPaths(m,n,row+1,col) + findPaths(m,n,row,col+1);
    }

};

3. Efficient Solution using memoization

Key concept

First, it is good to remind ourself about the purpose of implementing memoization. Why would we want to do this?

The definition of memoization from Wikipedia:

In computing, memoization or memoisation is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again.

So our goal is to store the result from the previous result to prevent redundant function calls. But there is one thing important to know before you implement the memoization: Will this leverage up our time complexity by sacrificing our space complexity?

For this specific problem, the answer is "yes." We are calling too many redundant function calls while we are scanning bottom and right points and we want to avoid it so that the program passes for the heavier test cases. I made a diagram that explains how memoization can make our code more efficient. Link to PDF

Code implementation

Link to the solution