Though used to doing Machine Learning works in Python, I have never tried Machine Learning dev work in Julia. I know there are already mature tools in Julia for Machine Leaning, however, I feel it necessary for me to do some basic exercises by myself in order to get a better understanding of Julia basics. Thus I tried this afternoon a simple Linear Regression experiment.
Firstly, I need to know how to solve optimization problems (LP, QP, SQP, etc) in Julia. Thanks to google, I quickly learned about the Optim module after a simple search. It is also for this exercise that I have done chart plot for the first time in Julia. Below is the chart I have plotted in this Linear Regression experiment.
Now I would like to share my code of this exercise:
using Random
using Optim
using Plots
## function for generating samples
# n: number of the sample
# b0 b1: linear params
# err: noise level
# seed: seed for random
function get_simple_regression_samples(n, b0=-0.3, b1=0.5, err=0.08, seed=nothing)
if seed!=nothing
Random.seed!(seed)
end
trueX = Random.rand(Float64, n)*2
trueX = trueX.- 1.0
trueT = (b1*trueX).+b0
return (trueX, trueT+randn(n)*err)
end
# now we obtain a batch of our sample points and print them
(x, y) = get_simple_regression_samples(20)
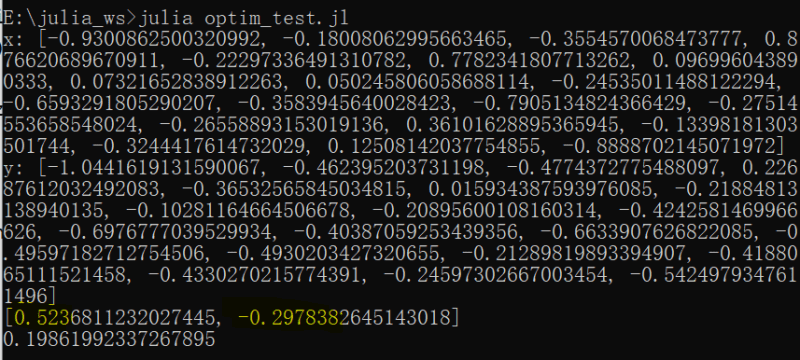
println("x: $x")
println("y: $y")
# plot the samples as scatter points
gr() # Set the backend to GR
# plot our samples using GR
display(plot(x,y ,seriestype=:scatter, title="Sample points"))
## now do the linear regression stuff
# a is the two coefficients that we want to get , ideal solution should be (0.5, -0.3)
# func(a): (Y_estim - y).T * (Y_estim - y) where Y_estim = (a1*x+a2)
func(a) = sum(((a[1]*x).+a[2] - y) .* ((a[1]*x).+a[2] - y))
# pass the function and the initial vector to optimization solver
res = optimize(func, [1.0,1.0])
# get the solution that minimizes the func
sol = Optim.minimizer(res)
println(sol)
# get the minimized value of the func
minval = Optim.minimum(res)
println(minval)
Then execute this script and I got the solution:
The real coefficients for generating the samples are [0.5, -0.3] and my script has solved it as [0.52368, -0.29784]. Wonderful!




Top comments (0)