The square loss function is the average of squared differences between the actual and the predicted values. the squared error is one of the most important functions in machine learning. It is used to train linear regression problems and certain neural networks.
In this problem, there are 3 power lines and our task is to place the house at a point where it is the most cost-effective.
Firstly, let's take the first power line. Where the house be situated to get the least cost? Obviously, where the distance is zero, so that we get zero cost.
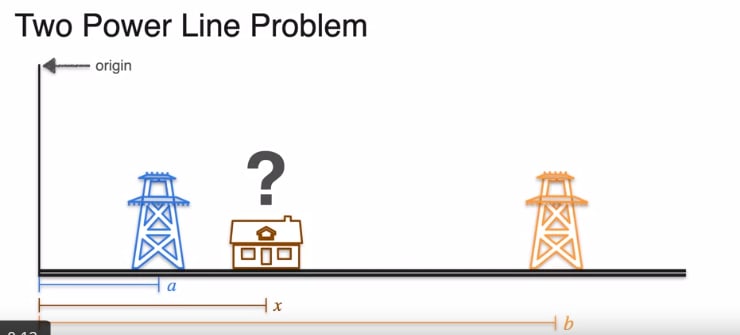
Now, let's bring another power line to the discussion.
Let, a= the distance of pl1 from origin
b= the distance of pl2 from origin
x= the distance of the house from origin
So, we can see the cost of connecting both of the powerlines is quite the same when the house is placed in the middle.
We don't want any of these above situations cause the cost area is very big.
We see that the tangent is zero in the lowest point. (x-a)^2 +(x-b)^2 is the cost function here, the derivate of this function is-
So, if the house is placed between two poles the cost will be minimized.
Now, let's see what happens if a 3rd powerline is in the scene,
Again, if we repeat the same procedure,
If we sum the heights of the three parabolas, we get the black parabola.
finding the derivative of the cost function-
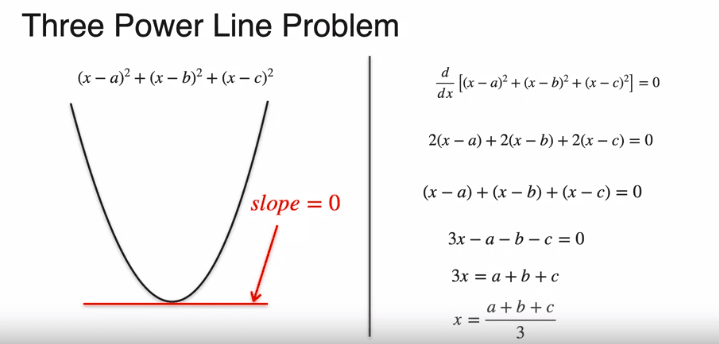
So, the generalized solution is-

Finally, the solution would be to put the house in the average of the coordinates of all the power lines. And this is the square loss function.
**The pictures are taken from different source.















Top comments (0)