Asymptotic Notation (Part 2)

Welcome back for part 2 for our introduction to Asymptotic Notation! Let's resume by talking about common runtimes:

Common Runtimes

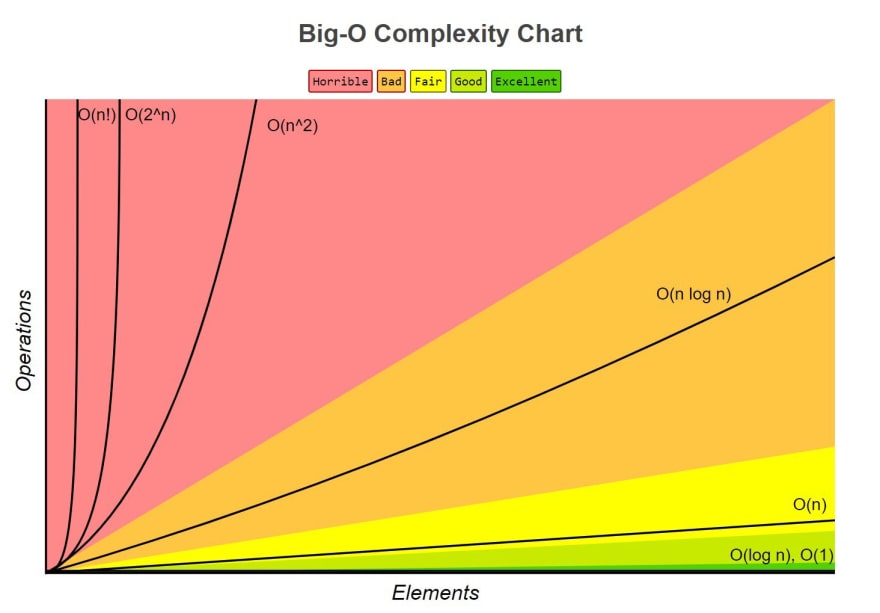
Before we delve into the multiple runtime cases, let’s see the different common runtimes a program could have. Below is a list of common runtimes that run from fastest to slowest.

Θ(1). This is constant runtime. This is the runtime when a program will always do the same thing regardless of the input. For instance, a program that only prints “hello, world” runs in Θ(1) because the program will always just print “hello, world”.

Θ(log N). This is logarithmic runtime. You will see this runtime in search algorithms.

Θ(N). This is linear runtime. You will often see this when you have to iterate through an entire dataset.

Θ(N*logN). You will see this runtime in sorting algorithms.
Θ(N2). This is an example of a polynomial runtime. You will see this runtime when you have to search through a two-dimensional dataset (like a matrix) or nested loops.

Θ(2N). This is exponential runtime. You will often see this runtime in recursive algorithms (Don’t worry if you don’t know what that is yet!).

Θ(N!). This is factorial runtime. You will often see this runtime when you have to generate all of the different permutations of something. For instance, a program that generates all the different ways to order the letters “abcd” would run in this runtime.

_{Image credits to Towards Data Science}

Big Omega (Ω) and Big O (O)

Sometimes, a program may have a different runtime for the best case and worst case. For instance, a program could have a best case runtime of Θ(1) and a worst case of Θ(N). We use a different notation when this is the case. We use big Omega or Ω to describe the best case and big O or O to describe the worst case. Take a look at the following pseudocode that returns True if 12 is in the list and False otherwise:

Function with input that is a list of size N:
    For each value in the list:
        If value is equal to 12:
            Return True
    Return False

How many times will the loop iterate? Let’s take a list of size 1000. If the first value in the list was 12, then the loop would only iterate once. However, if 12 wasn’t in the list at all, the loop would iterate 1000 times. If the input was a list of size N, the loop could iterate anywhere from 1 to N times depending on where 12 is in the list (or if it’s in the list at all). Thus, in the best case, it has a constant runtime and in the worst case it has a linear runtime.

There are many ways we could describe the runtime of this program:

• This program has a best case runtime of Θ(1).
• This program has a worst case runtime of Θ(N).
• This program has a runtime of Ω(1).
• This program has a runtime O(N).

You may be tempted to say the following:

• This program has a runtime of Θ(N).

However, this is not true because the program does not have a linear runtime in every case, only the worst case.

In fact, when describing runtime, people typically discuss the worst case because you should always prepare for the worst case scenario! Often times, in technical interviews, they will only ask you for the big O of a program.

Adding Runtimes

Sometimes, a program has so much going on that it’s hard to find the runtime of it. Take a look at the pseudocode program that first prints all the positive values up to N and then returns the number of times it takes to divide N by 2 until N is 1.

Function that takes a positive integer N:
    Set a variable i equal to 1
    Loop until i is equal to N:
        Print i
        Increment i

    Set a count variable to 0
    Loop while N is not equal to 1:
        Increment count
        N = N/2
    Return count

Rather than look at this program all at once, let’s divide into two chunks: the first loop and the second loop.

• In the first loop, we iterate until we reach N. Thus the runtime of the first loop is Θ(N).
• However, the second loop, as demonstrated in a previous exercise, runs in Θ(log N). Now, we can add the runtimes together, so the runtime is Θ(N) + Θ(log N).

However, when analyzing the runtime of a program, we only care about the slowest part of the program, and because Θ(N) is slower than Θ(log N), we would actually just say the runtime of this program is Θ(N). It is also appropriate to say the runtime is O(N) because if it runs in Θ(N) for every case, then it also runs in Θ(N) for the worst case. Most of the time people will just use big O notation.