Pascal's Triangle

Introduction

In mathematics, Pascal's triangle is triangular array of binomial coefficient.
below you can see how it looks like..

    1
   1 1
  1 2 1
 1 3 3 1
1 4 6 4 1

How to Build it?

First of all start with "1" and second rows as "1 1" then we can clearly see every element in next rows(except 1) if sum of two elements from above row. (i.e, 1+1=2, 1+2=3, 1+3=4) and with this rules we can create pascal's triangle of n rows.
Below is visual of how it will look like,

Formula

• [ ] let's take 0th row as first row and 0th column as first column, so we can get each value using formula where n is row number and k is column number. so for finding 1st(0 indexed) element in 2nd row we can write 2C1 which will give 2.

• [ ] There is one another technique, in which we need to solve (x + y)^n for nth row, if we solve (x +y)² then we will get 2nd row as coefficient of x and y in this solved formula which is x² + 2xy + y² . coefficients are (1 ,2 , 1) which is second row in pascal's triangle.

Implementation

So it is time to code let's see how we can implement it which some different approaches.
Approach 1 : nCr formula

#include<iostream>
using namespace std;

// return Factorial of val
int fact(int val){
    int ans = 1;
    for(int i=1;i<=val;i++){
        ans = ans* i;
    }
    return ans;
}
// return next value in pascal triangle
int nextval(int row, int col){
    int result;
    result = fact(row) / (fact(col)* fact(row-col));
    return result;
}
int main(){
    int n = 5; // creating pascal's triangle of 5 rows
    for (int i=0;i<n;i++){
        for(int j=0;j<=i;j++){
            cout << nextval(i,j) << " ";
        }
        cout << endl;
    }
    return 0;
}

Approach 2: Another Formula

#include<iostream>
using namespace std;
int main(){
    int rows = 5;

    for (int i=1;i<=rows;i++){
        int nCr = 1;
        cout << 1 << " ";
        for(int j=1;j<i;j++){
            nCr = nCr *(i-j)/j;
            cout << nCr << " ";
        }
        cout << endl;
    }
    return 0;
}

Approach 3: Using Vector for storing sum of two elements of previous row,

#include<iostream>
#include<vector>
using namespace std;
vector<vector<int>> pascal_triangle(int numRows) {
    vector<vector<int>> result(numRows);
    for(int i=0;i<numRows;i++){
        result[i].resize(i+1);
        result[i][0]=result[i][i]=1;

        for(int j=1;j<i;j++){
            result[i][j] = result[i-1][j] + result[i-1][j-1];
        }
    }
    return result;
}
void print(vector<vector<int>> result){
    for(int i=0;i<result.size();i++){
        for(int j=0;j<result[i].size();j++){
            cout << result[i][j] << " ";
        }
        cout << endl;
    }
}
int main(){
    int n=10;
    vector<vector<int>> result = pascal_triangle(n);
    print(result);
    return 0;
}

Approach 4 : Python3
when we concatenate [1] and [0] like [1] + [0] and [0] + [1] then we get [1,0] and [0,1] , now sum of every element of list1 and list2 will be [1,1] which if second row of pascal triangle now this same process with [1,1] then we'll get [1,1,0] and [0,1,1] then [1,2,1] , after repeating this process we can get pascal's triangle of n rows.

def pascal_triangle(numRows):
    ans = [[1]]
    for _ in range(1,numRows):
        a = ans[-1] + [0]
        b = [0] + ans[-1]
        sum_ab = [x+y for (x,y) in zip(a,b)]
        ans.append(sum_ab)
    # print(ans)
    return ans

result = pascal_triangle(5)
for i in result:
    print(i)

There are still other implementation of pascal's triangle , if you know any then let me know in comment box.

Some amazing facts

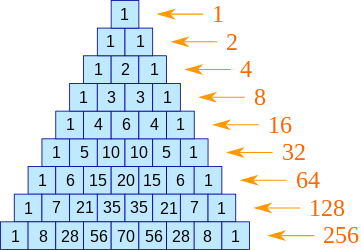
• [ ] if you have noticed if we sum of element in row then we'll get 2^n , where n is row number in that pascal's triangle. ( 1 = 2° , 1+1 = 2 , 1+2+1 = 2² )

• [ ] if we take whole row as one number then it is power of 11, ( 11° = 1, 11 = 1 1, 11² = 1 2 1 )
  

• [ ] Also there are some other patterns in pascal's triangle which you can see in below image,
  

References

• [ ] https://www.mathsisfun.com/pascals-triangle.html
• [ ] https://en.wikipedia.org/wiki/Pascal%27s_triangle

Thank You 😊😊